6.2 How Enzymes Work
The enzymatic catalysis of reactions is essential to living systems. Under biologically relevant conditions, uncatalyzed reactions tend to be slow — most biological molecules are quite stable in the neutral-pH, mild-temperature, aqueous environment inside cells. Reactions required to digest food, send nerve signals, or contract a muscle simply do not occur at a useful rate without catalysis.
The distinguishing feature of an enzyme-catalyzed reaction is that it takes place within the confines of a pocket on the enzyme called the active site (Fig. 6-1). The active site provides a specific environment, customized by evolution, in which a given reaction can occur more rapidly. The molecule that is bound in the active site and acted upon by the enzyme is called the substrate. The surface of the active site is lined with amino acid residues with substituent groups that bind the substrate and catalyze its chemical transformation. Often, the active site encloses a substrate, sequestering it completely from solution. The enzyme-substrate complex is central to the action of enzymes. It is also the starting point for mathematical treatments that define the kinetic behavior of enzyme-catalyzed reactions and for theoretical descriptions of enzyme mechanisms.
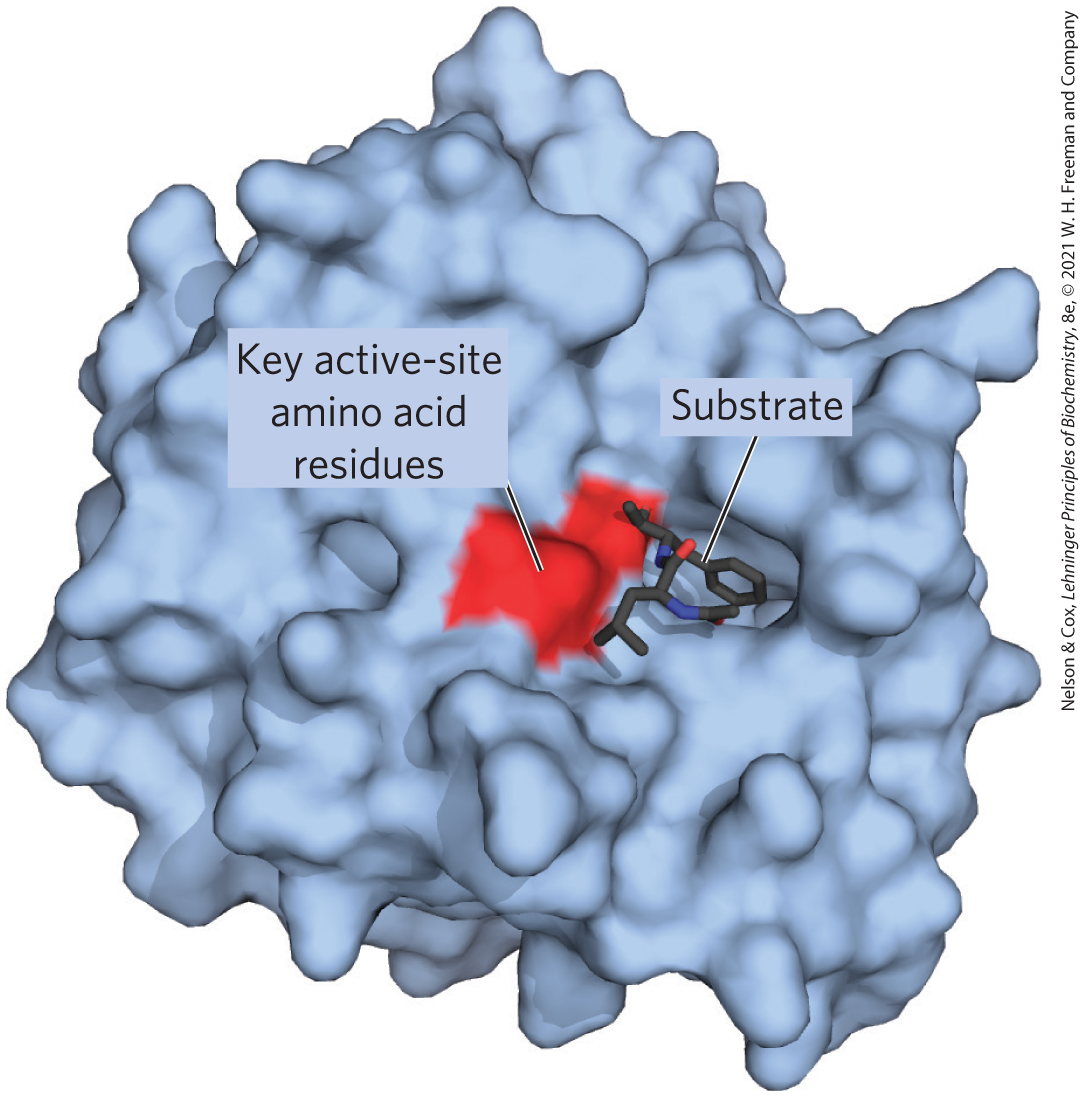
FIGURE 6-1 Binding of a substrate to an enzyme at the active site. The enzyme chymotrypsin with bound substrate. Some key active-site amino acid residues appear as a red splotch on the enzyme surface. [Data from PDB ID 7GCH, K. Brady et al., Biochemistry 29:7600, 1990.]
Enzymes Affect Reaction Rates, Not Equilibria
A simple enzymatic reaction might be written
(6-1)
where E, S, and P represent the enzyme, substrate, and product; ES and EP are transient complexes of the enzyme with the substrate and with the product.
To understand catalysis, we must first appreciate the important distinction between reaction equilibria and reaction rates. The function of a catalyst is to increase the rate of a reaction. Catalysts do not affect reaction equilibria. (Recall that a reaction is at equilibrium when there is no net change in the concentrations of reactants or products.) Any reaction, such as , can be described by a reaction coordinate diagram (Fig. 6-2), a picture of the energy changes during the reaction. As discussed in Chapter 1, energy in biological systems is described in terms of free energy, G. In the coordinate diagram, the free energy of the system is plotted against the progress of the reaction (the reaction coordinate). The starting point for either the forward reaction or the reverse reaction is called the ground state, the contribution to the free energy of the system by an average molecule (S or P) under a given set of conditions.
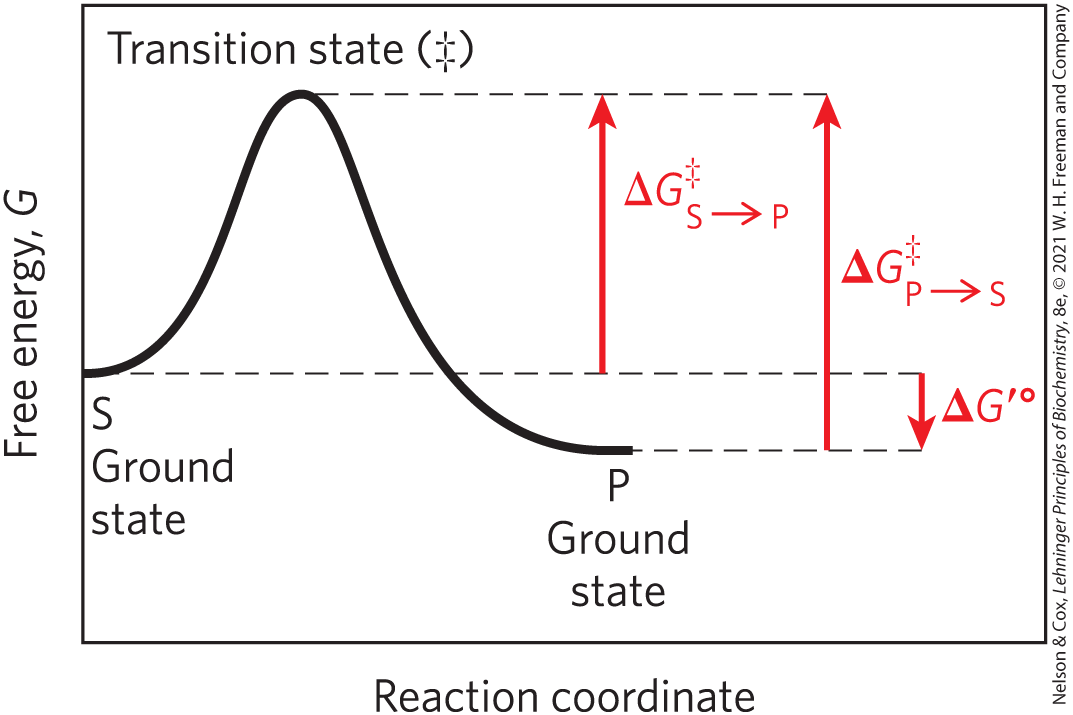
FIGURE 6-2 Reaction coordinate diagram. The free energy of the system is plotted against the progress of the reaction . Such a diagram describes the energy changes during the reaction. The horizontal axis (reaction coordinate) reflects the progressive chemical changes (e.g., bond breakage or formation) as S is converted to P. The activation energies, , for the and reactions are indicated. is the overall standard free-energy change in the direction .
Key convention
To describe the free-energy changes for reactions, chemists define a standard set of conditions (temperature of 298 K; partial pressure of each gas, 1 atm, or 101.3 kPa; concentration of each solute, 1 m), and express the free-energy change for a reacting system under these conditions as , the standard free-energy change. Because biochemical systems commonly involve concentrations far below 1 m, biochemists define a biochemical standard free-energy change, , the standard free-energy change at pH 7.0; we employ this definition throughout the book. A more complete definition of is given in Chapter 13.
The equilibrium between S and P reflects the difference in the free energies of their ground states. In the example shown in Figure 6-2, the free energy of the ground state of P is lower than that of S, so for the reaction is negative (the reaction is exergonic) and at equilibrium there is more P than S (the equilibrium favors P).
A favorable equilibrium does not mean that the conversion will occur at a rapid or even detectable rate. The rate of a reaction is instead dependent on an entirely different parameter, the energy barrier between S and P. That barrier consists of the energy required for alignment of reacting groups, formation of transient unstable charges, bond rearrangements, and other transformations required for the reaction to proceed in either direction. This is illustrated by the energy “hill” in Figures 6-2 and 6-3. To undergo reaction, the molecules must overcome this barrier and therefore must be raised to a higher energy level. At the top of the energy hill is a point at which decay to the S or P state is equally probable (it is downhill either way). This is called the transition state, often symbolized by a double dagger (‡). The transition state is not a chemical species with any significant stability and should not be confused with a reaction intermediate (such as ES or EP). It is simply a fleeting molecular moment in which events such as bond breakage, bond formation, and charge development have proceeded to the precise point at which decay to substrate and decay to product are equally likely.
The difference between the energy level of the ground state and the energy level of the transition state is the activation energy, . The rate of a reaction reflects this activation energy: a higher activation energy corresponds to a slower reaction. Lowering the activation energy increases the rate of reaction. Reaction rates can be increased by raising the temperature and/or pressure, thereby increasing the number of molecules with sufficient energy to overcome the energy barrier. Alternatively, the activation energy can be lowered, and reaction rate increased, by adding a catalyst (Fig. 6-3).
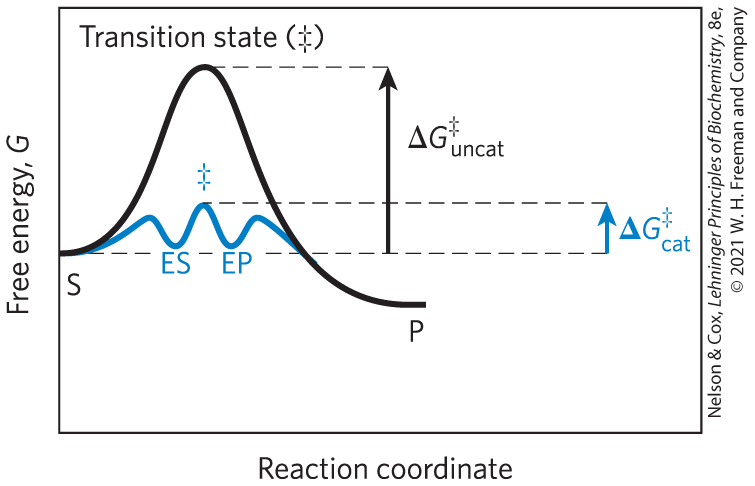
FIGURE 6-3 Reaction coordinate diagram comparing enzyme-catalyzed and uncatalyzed reactions. In the reaction , the ES and EP intermediates occupy minima in the energy progress curve of the enzyme-catalyzed reaction. The terms and correspond to the activation energy for the uncatalyzed reaction and the overall activation energy for the catalyzed reaction, respectively. The activation energy is lower when the enzyme catalyzes the reaction.
Catalysts do not affect reaction equilibria. The bidirectional arrows in Equation 6-1 make this important point: any enzyme that catalyzes the reaction also catalyzes the reaction . The role of enzymes is to accelerate the interconversion of S and P. The enzyme is not used up in the process, and the equilibrium point is unaffected. However, the reaction reaches equilibrium much faster when the appropriate enzyme is present, because the rate of the reaction is increased.
This relationship between reaction rate and activation energy is illustrated by the process introduced at the beginning of the chapter: the conversion of sucrose and oxygen to carbon dioxide and water:
This conversion, which takes place through a series of separate reactions, has a very large and negative , and at equilibrium the amount of sucrose present is negligible. Yet sucrose is a stable compound, because the activation energy barrier that must be overcome before sucrose reacts with oxygen is quite high. Sucrose can be stored in a container with oxygen almost indefinitely without reacting. In cells, however, sucrose is readily broken down to and in a series of reactions catalyzed by enzymes. These enzymes not only accelerate the reactions, they organize and control them so that much of the energy released is recovered in other chemical forms and made available to the cell for other tasks. The reaction pathway by which sucrose (and other sugars) is broken down is the primary energy-yielding pathway for cells, and the enzymes of this pathway allow the reaction sequence to proceed on a biologically useful (millisecond) time scale.
Any reaction may have several steps, involving the formation and decay of transient chemical species called reaction intermediates.i A reaction intermediate is any species on the reaction pathway that has a finite chemical lifetime (longer than a molecular vibration, second). When the reaction is catalyzed by an enzyme, the ES and EP complexes can be considered intermediates, even though S and P are stable chemical species (Eqn 6-1); the ES and EP complexes occupy valleys in the reaction coordinate diagram (Fig. 6-3). Additional, less-stable chemical intermediates often exist in the course of an enzyme-catalyzed reaction. The interconversion of two sequential reaction intermediates thus constitutes a reaction step. When several steps occur in a reaction, the overall rate is determined by the step (or steps) with the highest activation energy; this is called the rate-limiting step. In a simple case, the rate-limiting step is the highest-energy point in the diagram for interconversion of S and P. In practice, the rate-limiting step can vary with reaction conditions, and for many enzymes several steps may have similar activation energies, which means they are all partially rate-limiting.
Activation energies are energy barriers to chemical reactions. These barriers are crucial to life itself. Without such energy barriers, complex macromolecules would revert spontaneously to much simpler molecular forms, and the complex and highly ordered structures and metabolic processes of cells could not exist. Over the course of evolution, enzymes have developed to lower activation energies selectively, and thus increase rates, for reactions that are needed for cell survival.
Reaction Rates and Equilibria Have Precise Thermodynamic Definitions
Reaction equilibria are inextricably linked to the standard free-energy change for the reaction, , and reaction rates are linked to the activation energy, . A basic introduction to these thermodynamic relationships is the next step in understanding how enzymes work.
An equilibrium such as is described by an equilibrium constant, , or simply K (p. 23). Under the standard conditions used to compare biochemical processes, an equilibrium constant is denoted (or ):
(6-2)
From thermodynamics, the relationship between and can be described by the expression
(6-3)
where R is the gas constant, 8.315 J/mol·K, and T is the absolute temperature, . Equation 6-3 is developed and discussed in more detail in Chapter 13. The important point here is that the equilibrium constant is directly related to the overall standard free-energy change for the reaction (Table 6-4). A large negative value for reflects a favorable reaction equilibrium (one in which there is much more product than substrate at equilibrium) — but as already noted, this does not mean the reaction will proceed at a rapid rate.
| 34.2 | |
| 28.5 | |
| 22.8 | |
| 17.1 | |
| 11.4 | |
| 5.7 | |
| 1 | 0.0 |
| −5.7 | |
| −11.4 | |
| −17.1 | |
Note: The relationship is calculated from ln (Eqn 6-3). |
|
The rate of any reaction is determined by the concentration of the reactant (or reactants) and by a rate constant, usually denoted by k. For the unimolecular reaction , the rate (or velocity) of the reaction, V — representing the amount of S that reacts per unit of time — is expressed by a rate equation:
(6-4)
In this reaction, the rate depends only on the concentration of S. This is called a first-order reaction. The factor k is a proportionality constant that reflects the probability of reaction under a given set of conditions (pH, temperature, and so forth). Here, k is a first-order rate constant and has units of reciprocal time, such as . If a first-order reaction has a rate constant k of , this may be interpreted (qualitatively) to mean that 3% of the available S will be converted to P in 1 second. A reaction with a rate constant of will be over in a small fraction of a second. If a reaction rate depends on the concentration of two different compounds, or if the reaction is between two molecules of the same compound, the reaction is second order and k is a second-order rate constant, with units of . The rate equation then becomes
(6-5)
From transition-state theory we can derive an expression that relates the magnitude of a rate constant to the activation energy:
(6-6)
where k is the Boltzmann constant and h is Planck’s constant. The important point is that the relationship between the rate constant k and the activation energy is inverse and exponential. In simplified terms, this is the basis for the statement that a lower activation energy means a faster reaction rate — and lowering activation energies is what enzymes do.
Now we turn from what enzymes do to how they do it.
A Few Principles Explain the Catalytic Power and Specificity of Enzymes
Enzymes are extraordinary catalysts. The rate enhancements they bring about are in the range of 5 to 17 orders of magnitude (Table 6-5). Enzymes are also very specific, readily discriminating between substrates with quite similar structures. How can these enormous and highly selective rate enhancements be explained? What is the source of the energy for the dramatic lowering of the activation energies for specific reactions?
| Cyclophilin | |
| Carbonic anhydrase | |
| Triose phosphate isomerase | |
| Carboxypeptidase A | |
| Phosphoglucomutase | |
| Succinyl-CoA transferase | |
| Urease | |
| Orotidine monophosphate decarboxylase |
The answer to these questions has two distinct but interwoven parts. The first lies in the noncovalent interactions between enzyme and substrate. What really sets enzymes apart from most other catalysts is the formation of a specific ES complex. The interaction between substrate and enzyme in this complex is mediated by the same forces that stabilize protein structure, including hydrogen bonds, ionic interactions, and the hydrophobic effect (Chapter 4). Formation of each weak interaction in the ES complex is accompanied by release of a small amount of free energy that stabilizes the interaction. The energy derived from noncovalent enzyme-substrate interaction is called binding energy, . Its significance extends beyond a simple stabilization of the enzyme-substrate interaction. As we will see, binding energy is a major source of free energy used by enzymes to lower the activation energies of reactions.
The second part of the explanation lies in covalent interactions between enzyme and substrate, plus a few additional chemical catalytic mechanisms. Chemical reactions of many types take place between substrates and enzymes’ functional groups (specific amino acid side chains, metal ions, and coenzymes). Catalytic functional groups on an enzyme may form a transient covalent bond with a substrate and activate it for reaction, or a group may be transiently transferred from the substrate to the enzyme. In many cases, these reactions occur only in the enzyme active site. Covalent interactions between enzymes and substrates lower the activation energy (and thereby accelerate the reaction) by providing an alternative, lower-energy reaction path. Metal ions facilitate additional mechanisms of catalysis that do not involve covalent interactions.
We now consider noncovalent contributions to catalysis and the additional chemical mechanisms in turn.
Noncovalent Interactions between Enzyme and Substrate Are Optimized in the Transition State
How does an enzyme use noncovalent binding energy to lower the activation energy for a reaction? Formation of the ES complex is not the explanation in itself, although some of the earliest considerations of enzyme mechanisms began with this idea. Studies on enzyme specificity carried out by Emil Fischer led him to propose, in 1894, that enzymes were structurally complementary to their substrates, so that they fit together like a lock and key (Fig. 6-4). This elegant idea, that a specific (exclusive) interaction between two biological molecules is mediated by molecular surfaces with complementary shapes, has greatly influenced the development of biochemistry. However, the “lock and key” hypothesis can be misleading when applied to enzymatic catalysis. An enzyme completely complementary to its substrate would be a very poor enzyme, as we can demonstrate.
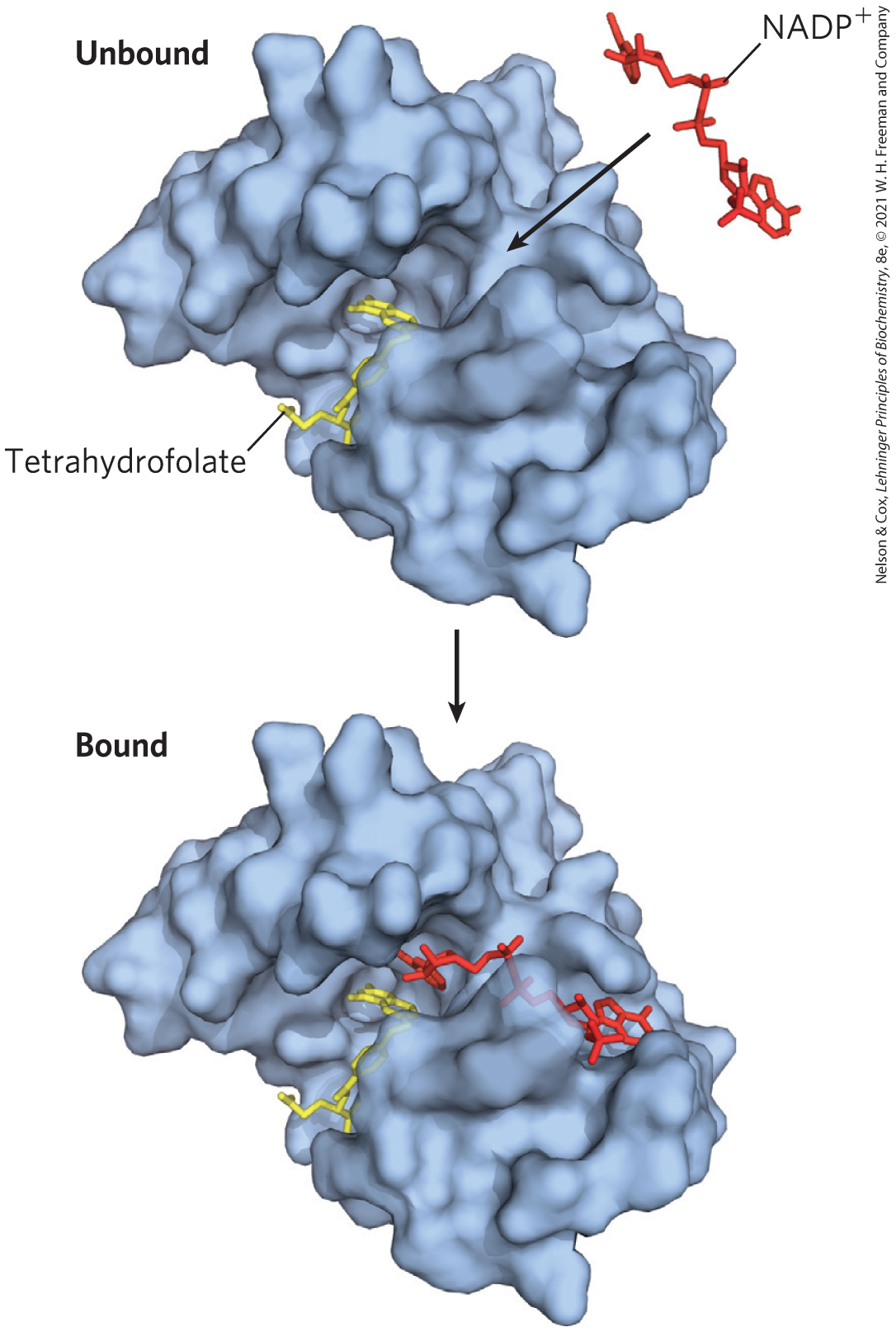
FIGURE 6-4 Complementary shapes of a substrate and its binding site on an enzyme. The enzyme dihydrofolate reductase with its substrate , unbound and bound; another bound substrate, tetrahydrofolate, is also visible. In this model, the binds to a pocket that is complementary to it in shape and ionic properties, an illustration of Emil Fischer’s “lock and key” hypothesis of enzyme action. In reality, the complementarity between protein and ligand (in this case, substrate) is rarely perfect, as we saw in Chapter 5. [Data from PDB ID 1RA2, M. R. Sawaya and J. Kraut, Biochemistry 36:586, 1997.]
Consider an imaginary reaction, the breaking of a magnetized metal stick. The uncatalyzed reaction is shown in Figure 6-5a. Let’s examine two imaginary enzymes — two “stickases” — that could catalyze this reaction, both of which employ magnetic forces as a paradigm for the binding energy used by real enzymes. We first design an enzyme perfectly complementary to the substrate (Fig. 6-5b). The active site of this stickase is a pocket lined with magnets. To react (break), the stick must reach the bent transition state of the reaction. However, the snug fit of the stick in this active site means that magnets hinder the required bending. Such an enzyme impedes the reaction, stabilizing the substrate instead. In a reaction coordinate diagram (Fig. 6-5b), this kind of ES complex would correspond to an energy trough from which the substrate would have difficulty escaping. Such an enzyme would be useless.
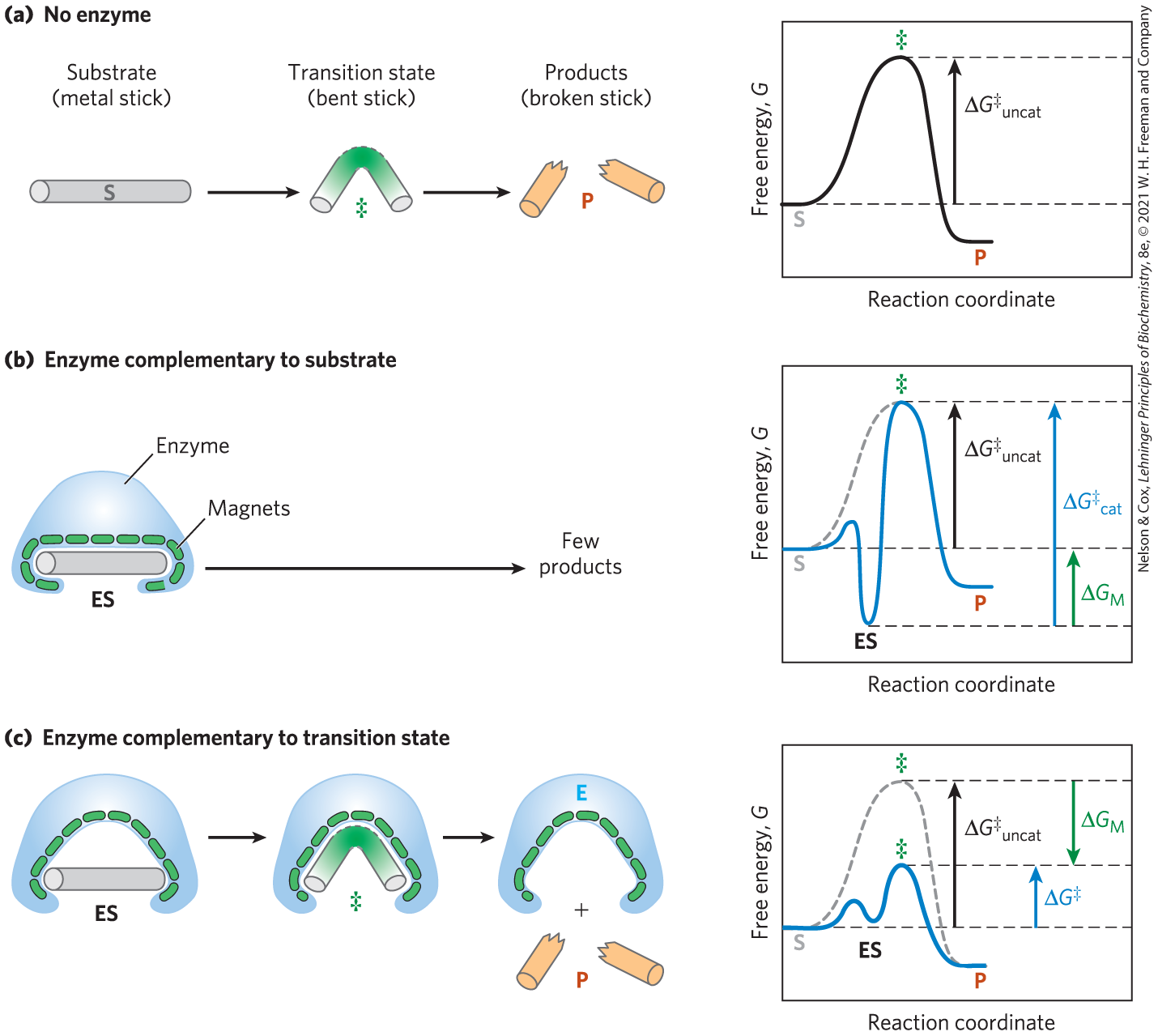
FIGURE 6-5 An imaginary enzyme (stickase) designed to catalyze breakage of a metal stick. (a) Before the stick is broken, it must first be bent (the transition state). In both stickase examples, magnetic interactions take the place of weak bonding interactions between enzyme and substrate. (b) A stickase with a magnet-lined pocket complementary in structure to the stick (the substrate) stabilizes the substrate. Bending is impeded by the magnetic attraction between stick and stickase. (c) An enzyme with a pocket complementary to the reaction transition state helps to destabilize the stick, contributing to catalysis of the reaction. The binding energy of the magnetic interactions compensates for the increase in free energy required to bend the stick. Reaction coordinate diagrams (right) show the energy consequences of complementarity to substrate versus complementarity to transition state (EP complexes are omitted). , the difference between the transition-state energies of the uncatalyzed and catalyzed reactions, is contributed by the magnetic interactions between the stick and stickase. When the enzyme is complementary to the substrate (b), the ES complex is more stable and has less free energy in the ground state than substrate alone. The result is an increase in the activation energy.
The modern notion of enzymatic catalysis, first proposed by Michael Polanyi (1921) and J. B. S. Haldane (1930), was elaborated by Linus Pauling in 1946 and by William P. Jencks in the 1970s: in order to catalyze reactions, an enzyme must be complementary to the reaction transition state. This means that optimal interactions between substrate and enzyme occur only in the transition state. Figure 6-5c demonstrates how such an enzyme can work. The metal stick binds to the stickase, but only a few of the possible magnetic interactions are used in forming the ES complex. The bound substrate must still undergo the increase in free energy needed to reach the transition state. Now, however, the increase in free energy required to draw the stick into a bent and partially broken conformation is offset, or “paid for,” by the magnetic interactions that form between our imaginary enzyme and substrate (analogous to the binding energy in a real enzyme) in the transition state. Many of these interactions involve parts of the stick that are distant from the point of breakage; thus, interactions between the stickase and nonreacting parts of the stick provide some of the energy needed to catalyze stick breakage. This “energy payment” translates into a lower net activation energy and a faster reaction rate.
Real enzymes work on an analogous principle. Some weak interactions are formed in the ES complex, but the full complement of such interactions between substrate and enzyme is formed only when the substrate reaches the transition state. The free energy (binding energy) released by the formation of these interactions partially offsets the energy required to reach the top of the energy hill. The summation of the unfavorable (positive) activation energy and the favorable (negative) binding energy results in a lower net activation energy (Fig. 6-6). Even on the enzyme, the transition state is not a stable species but a brief point in time that the substrate spends atop an energy hill. However, the enzyme-catalyzed reaction is much faster than the uncatalyzed process because the hill is much smaller. The important principle is that weak binding interactions between the enzyme and the substrate provide a substantial driving force for enzymatic catalysis. The groups on the substrate that are involved in these weak interactions can be at some distance from the bonds that are broken or changed. The weak interactions formed only in the transition state are those that make the primary contribution to catalysis.
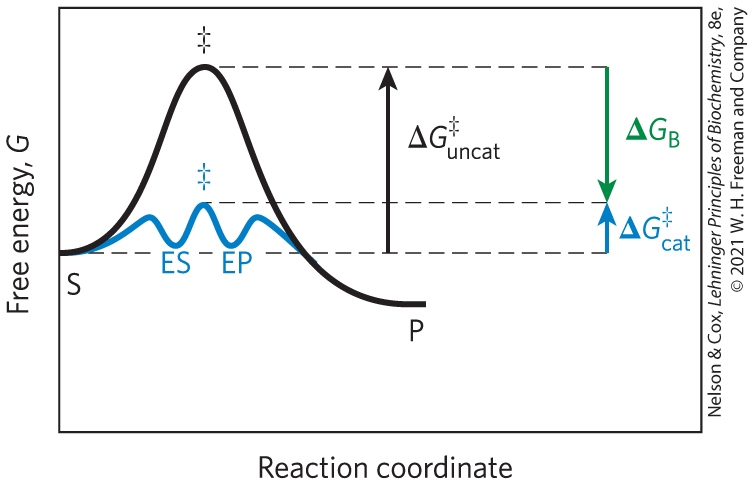
FIGURE 6-6 Role of binding energy in catalysis. To lower the activation energy for a reaction, the system must acquire an amount of energy equivalent to the amount by which is lowered. Much of this energy comes from binding energy, , contributed by formation of weak noncovalent interactions between substrate and enzyme in the transition state. The role of is analogous to that of in Figure 6-5.
The requirement for multiple weak interactions to drive catalysis is one reason why enzymes (and some coenzymes) are so large. An enzyme must provide functional groups for ionic, hydrogen-bond, and other interactions, and also must precisely position these groups so that binding energy is optimized in the transition state. Adequate binding is accomplished most readily by positioning a substrate in a cavity (the active site) where it is effectively removed from water. The size of proteins reflects the need for superstructure to keep interacting groups properly positioned and to keep the cavity from collapsing.
Can we demonstrate quantitatively that binding energy accounts for the huge rate accelerations brought about by enzymes? Yes. As a point of reference, Equation 6-6 allows us to calculate that must be lowered by about 5.7 kJ/mol to accelerate a first-order reaction by a factor of 10, under conditions commonly found in cells. The energy available from formation of a single weak interaction is generally estimated to be 4 to 30 kJ/mol. The overall energy available from many such interactions is therefore sufficient to lower activation energies by the 60 to 100 kJ/mol required to explain the large rate enhancements observed for many enzymes.
The same binding energy that provides energy for catalysis also gives an enzyme its specificity, the ability to discriminate between a substrate and a competing molecule. Conceptually, specificity is easy to distinguish from catalysis, but this distinction is much more difficult to make experimentally, because catalysis and specificity arise from the same phenomenon. If an enzyme active site has functional groups arranged optimally to form a variety of weak interactions with a particular substrate in the transition state, the enzyme will not be able to interact to the same degree with any other molecule. For example, if the substrate has a hydroxyl group that forms a hydrogen bond with a specific Glu residue on the enzyme, any molecule lacking a hydroxyl group at that particular position will be a poorer substrate for the enzyme. In general, specificity is derived from the formation of many weak interactions between the enzyme and its specific substrate molecule.
The importance of binding energy to catalysis can be readily demonstrated. For example, the glycolytic enzyme triose phosphate isomerase catalyzes the interconversion of glyceraldehyde 3-phosphate and dihydroxyacetone phosphate:
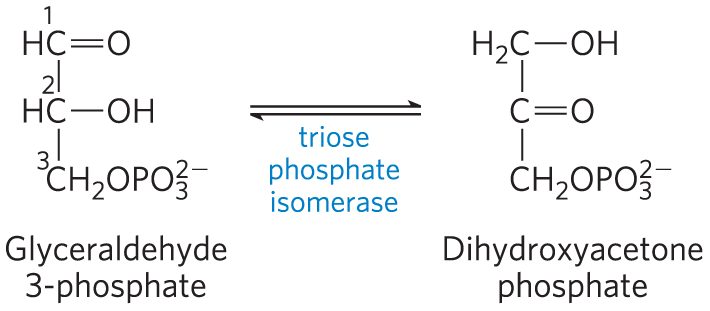
This reaction rearranges the carbonyl and hydroxyl groups on carbons 1 and 2. However, more than 80% of the enzymatic rate acceleration has been traced to enzyme-substrate interactions involving the phosphate group on carbon 3 of the substrate. This was determined by comparing the enzyme-catalyzed reactions with glyceraldehyde 3-phosphate and with glyceraldehyde (no phosphate group at position 3) as substrate.
The general principles outlined above can be illustrated by a variety of recognized catalytic mechanisms. These mechanisms are not mutually exclusive, and a given enzyme might incorporate several catalytic strategies in its overall mechanism of action.
Consider what needs to occur for a reaction to take place. Prominent physical and thermodynamic factors contributing to , the barrier to reaction, might include (1) the entropy of molecules in solution, which reduces the possibility that they will react together; (2) the solvation shell of hydrogen-bonded water that surrounds and helps to stabilize most biomolecules in aqueous solution; (3) the distortion of substrates that must occur in many reactions; and (4) the need for proper alignment of catalytic functional groups on the enzyme. Binding energy can be used to overcome all these barriers.
First, a large restriction in the relative motions of two substrates that are to react, or entropy reduction, is one obvious benefit of binding them to an enzyme. Binding energy constrains the substrates in the proper orientation to react — a substantial contribution to catalysis, because productive collisions between molecules in solution can be exceedingly rare. Substrates can be precisely aligned on the enzyme, with many weak interactions between each substrate and strategically located groups on the enzyme clamping the substrate molecules into the proper positions. Studies have shown that simply constraining the motion of two reactants can produce rate enhancements of many orders of magnitude (Fig. 6-7).
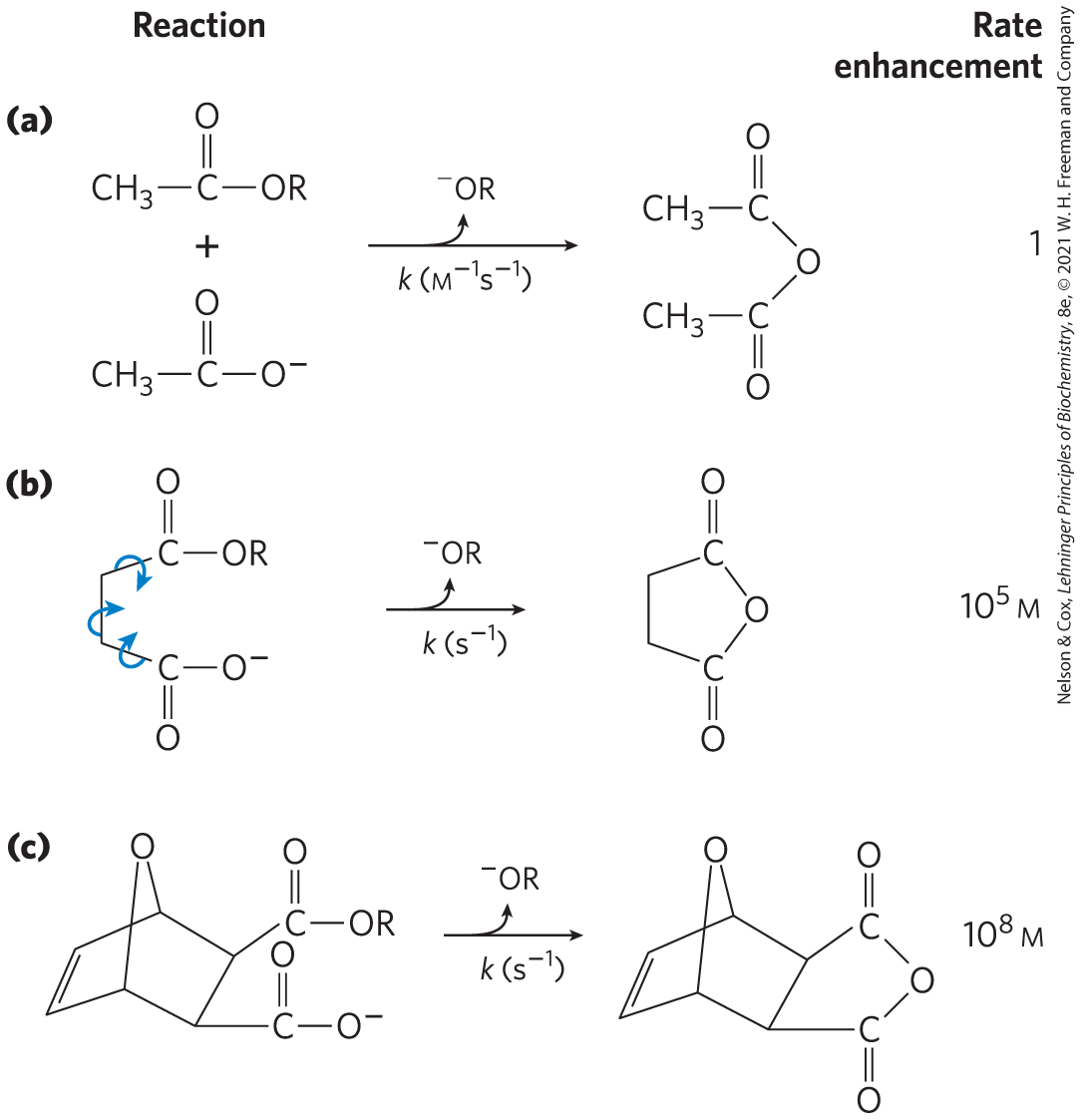
FIGURE 6-7 Rate enhancement by entropy reduction. Shown here are reactions of an ester with a carboxylate group to form an anhydride. The R group is the same in each case. (a) For this bimolecular reaction, the rate constant k is second order, with units of . (b) When the two reacting groups are in a single molecule, and thus have less freedom of motion, the reaction is much faster. For this unimolecular reaction, k has units of . Dividing the rate constant for (b) by the rate constant for (a) gives a rate enhancement of about . (The enhancement has units of molarity because we are comparing a unimolecular reaction and a bimolecular reaction.) Put another way, if the reactant in (b) were present at a concentration of 1 m, the reacting groups would behave as though they were present at a concentration of . Note that the reactant in (b) has freedom of rotation about three bonds (shown with curved arrows), but this still represents a substantial reduction of entropy over (a). If the bonds that rotate in (b) are constrained as in (c), the entropy is reduced further and the reaction exhibits a rate enhancement of relative to (a).
Second, in water, many organic molecules are surrounded by a solvation shell of structured water that can hinder reactions (see Fig. 2-8). Formation of weak bonds between substrate and enzyme results in desolvation of the substrate. Enzyme-substrate interactions replace most or all of the hydrogen bonds between the substrate and water that would otherwise impede reaction.
Third, binding energy involving weak interactions that are formed only in the reaction transition state helps to compensate thermodynamically for the unfavorable free-energy change associated with any distortion, primarily electron redistribution, that the substrate must undergo to react.
Finally, the enzyme itself usually undergoes a change in conformation when the substrate binds, induced by multiple weak interactions with the substrate. This is referred to as induced fit, a mechanism postulated by Daniel Koshland in 1958. The motions can affect a small part of the enzyme near the active site or can involve changes in the positioning of entire domains. Typically, a network of coupled motions occurs throughout the enzyme that ultimately brings about the required changes in the active site. Induced fit serves to bring specific functional groups on the enzyme into the proper position to catalyze the reaction. The conformational change also permits formation of additional weak bonding interactions in the transition state. In either case, the new enzyme conformation has enhanced catalytic properties. As we have seen, induced fit is a common feature of the reversible binding of ligands to proteins (Chapter 5). Induced fit is also important in the interaction of almost every enzyme with its substrate.
Covalent Interactions and Metal Ions Contribute to Catalysis
In most enzymes, noncovalent binding energy is just one of several contributors to the overall catalytic mechanism. Once a substrate is bound to an enzyme, properly positioned catalytic functional groups aid in the cleavage and formation of bonds by a variety of mechanisms, including general acid-base catalysis, covalent catalysis, and metal ion catalysis. The first two of these mechanisms are distinct from those based on binding energy, because they generally involve transient covalent interaction with a substrate or group transfer to or from a substrate.
General Acid-Base Catalysis
Transfer of a proton from one molecule to another is the single most common reaction in biochemistry. One or, often, many proton transfers occur in the course of most reactions that take place in cells. Many biochemical reactions occur through the formation of unstable charged intermediates that tend to break down rapidly to their constituent reactant species, impeding the forward reaction (Fig. 6-8). Charged intermediates can often be stabilized by the transfer of protons to form a species that breaks down more readily to products. These protons are transferred between an enzyme and a substrate or intermediate.
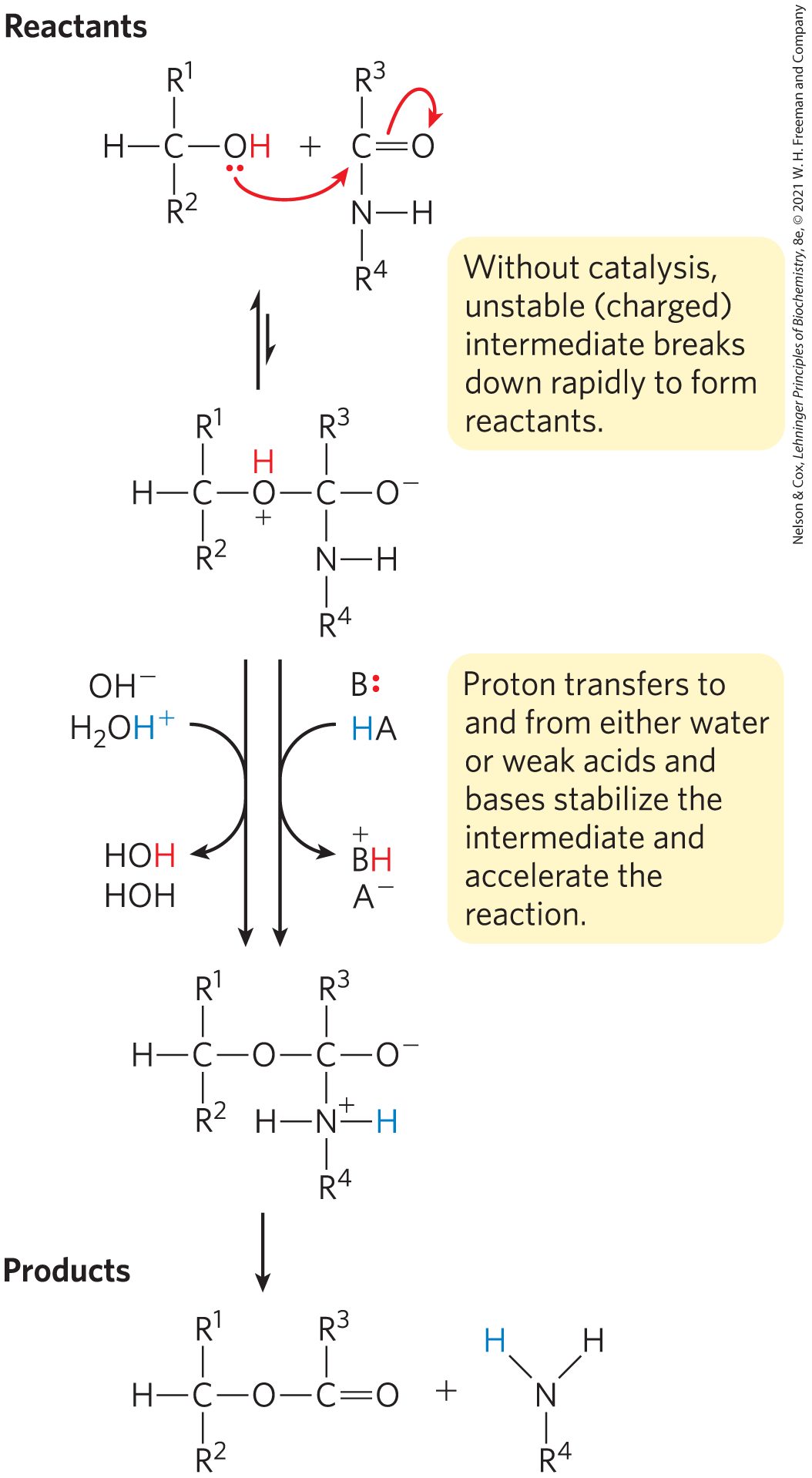
FIGURE 6-8 How a catalyst circumvents unfavorable charge development during cleavage of an amide. The hydrolysis of an amide bond, shown here, is the same reaction as that catalyzed by chymotrypsin and other proteases. Charge development is unfavorable and can be circumvented by donation of a proton by (specific acid catalysis) or HA (general acid catalysis), where HA represents any acid. Similarly, charge can be neutralized by proton abstraction by (specific base catalysis) or B: (general base catalysis), where B: represents any base.
The effects of catalysis by acids and bases are often studied using nonenzymatic model reactions, in which the proton donors or acceptors are either the constituents of water alone or other weak acids and bases. Catalysis of the type that uses only the or ions present in water is referred to as specific acid-base catalysis. However, a further increase in rate can often be afforded by the addition of weak acids and bases to the reaction. Many weak organic acids can supplement water as proton donors, or weak organic bases can supplement water as proton acceptors. The term general acid-base catalysis refers to proton transfers mediated by weak acids and bases other than water.
General acid-base catalysis becomes crucial in the active site of an enzyme, where water may not be available as a proton donor or acceptor. Several amino acid side chains can and do take on the role of proton donors and acceptors (Fig. 6-9). These groups can be precisely positioned in an enzyme active site to allow proton transfers, providing rate enhancements of the order of to . This type of catalysis occurs on the vast majority of enzymes.
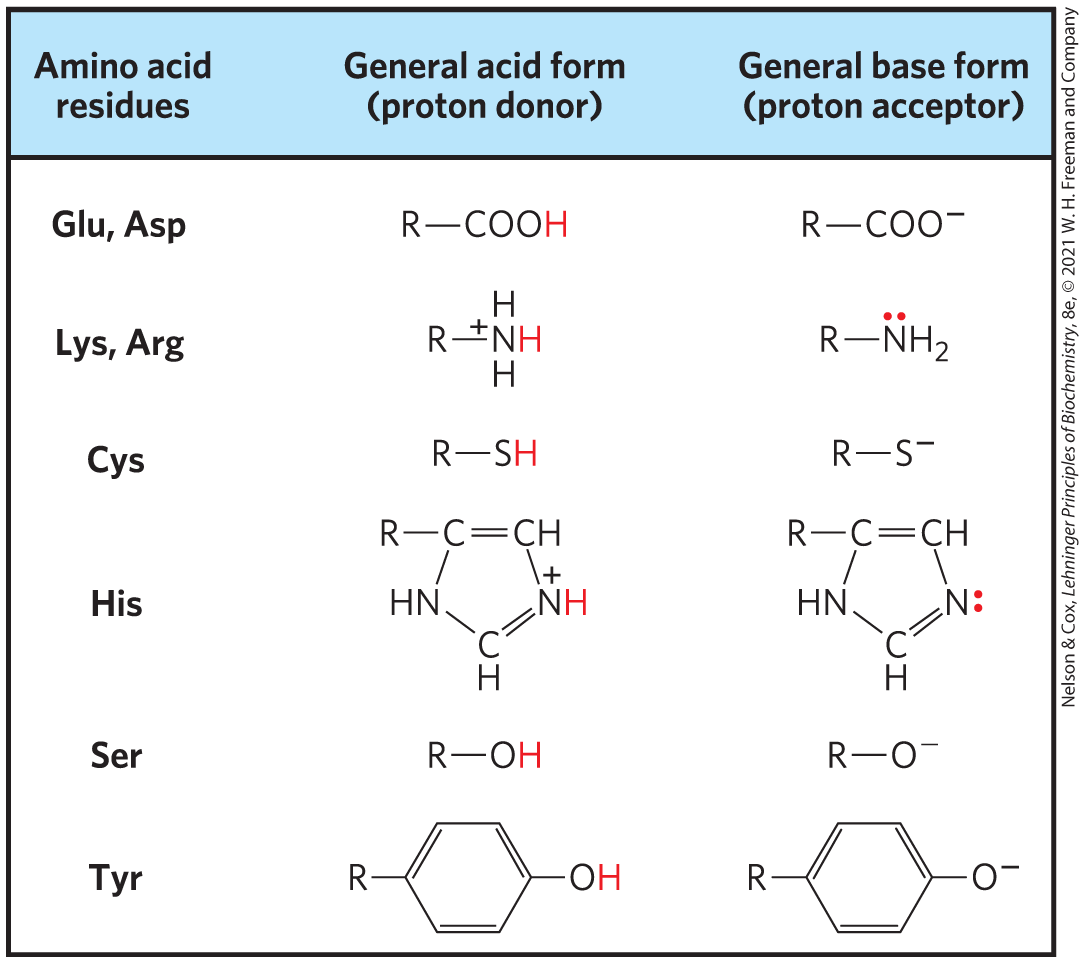
FIGURE 6-9 Amino acids in general acid-base catalysis. Many organic reactions that are used to model biochemical processes are promoted by proton donors (general acids) or proton acceptors (general bases). The active sites of some enzymes contain amino acid functional groups, such as those shown here, that can participate in the catalytic process as proton donors or proton acceptors.
Covalent Catalysis
In covalent catalysis, a transient covalent bond is formed between the enzyme and the substrate. Consider the hydrolysis of a bond between groups A and B:
In the presence of a covalent catalyst (an enzyme with a nucleophilic group X:) the reaction becomes
Formation and breakdown of a covalent intermediate creates a new pathway for the reaction, but catalysis results only when the new pathway has a lower activation energy than the uncatalyzed pathway. Both of the new steps must be faster than the uncatalyzed reaction. Several amino acid side chains, including all those in Figure 6-9, and the functional groups of some enzyme cofactors can serve as nucleophiles in the formation of covalent bonds with substrates. These covalent complexes always undergo further reaction to regenerate the free enzyme. The covalent bond formed between the enzyme and the substrate can activate a substrate for further reaction in a manner that is usually specific to the particular group or coenzyme.
Metal Ion Catalysis
Metals, whether tightly bound to the enzyme or taken up from solution along with the substrate, can participate in catalysis in several ways. Ionic interactions between an enzyme-bound metal and a substrate can help orient the substrate for reaction or stabilize charged reaction transition states. This use of weak bonding interactions between metal and substrate is similar to some of the uses of enzyme-substrate binding energy described earlier, and it can contribute to enzyme–transition state complementarity. Metals can also mediate oxidation-reduction reactions by reversible changes in the metal ion’s oxidation state. Nearly a third of all known enzymes require one or more metal ions for catalytic activity.
Most enzymes combine several catalytic strategies to bring about a rate enhancement. A good example is the use of covalent catalysis, general acid-base catalysis, and transition-state stabilization in the reaction catalyzed by chymotrypsin, detailed in Section 6.4.
SUMMARY 6.2 How Enzymes Work
- Enzymes are highly effective catalysts, commonly enhancing reaction rates by a factor of to . Enzyme-catalyzed reactions are characterized by the formation of a complex between substrate and enzyme (an ES complex). Substrate binding occurs in a pocket on the enzyme called the active site.
- The function of enzymes and other catalysts is to lower the activation energy, , for a reaction and thereby enhance the reaction rate. The equilibrium of a reaction is unaffected by the enzyme.
- Reaction equilibria are described by equilibrium constants, , which are related to the biochemical standard free-energy change . Reaction rates are described by rate constants, k, which are related to the activation energy .
- The extraordinary rate accelerations provided by enzymes are due to noncovalent binding energy supplemented by covalent interactions or metal ion catalysis.
- Noncovalent binding energy, , is maximized in the transition state of the catalyzed reaction. Enzyme–transition state complementarity is a fundamental principle of enzymatic catalysis. Noncovalent interactions may facilitate the path to the transition state, offsetting the energy required for activation, , by lowering substrate entropy, causing substrate desolvation, or causing a conformational change in the enzyme (induced fit). Binding energy also accounts for the exquisite specificity of enzymes for their substrates.
- General acid-base catalysis and covalent catalysis mechanisms contribute to the catalytic power of enzymes. Covalent interactions between the substrate and the enzyme, group transfers to and from the enzyme, and interactions with metal ions can provide a new, lower-energy reaction path.
 The distinguishing feature of an enzyme-catalyzed reaction is that it takes place within the confines of a pocket on the enzyme called the
The distinguishing feature of an enzyme-catalyzed reaction is that it takes place within the confines of a pocket on the enzyme called the  The function of a catalyst is to increase the rate of a reaction. Catalysts do not affect reaction equilibria. (Recall that a reaction is at equilibrium when there is no net change in the concentrations of reactants or products.) Any reaction, such as , can be described by a reaction coordinate diagram (
The function of a catalyst is to increase the rate of a reaction. Catalysts do not affect reaction equilibria. (Recall that a reaction is at equilibrium when there is no net change in the concentrations of reactants or products.) Any reaction, such as , can be described by a reaction coordinate diagram (
 Over the course of evolution, enzymes have developed to lower activation energies selectively, and thus increase rates, for reactions that are needed for cell survival.
Over the course of evolution, enzymes have developed to lower activation energies selectively, and thus increase rates, for reactions that are needed for cell survival. binding energy is a major source of free energy used by enzymes to lower the activation energies of reactions.
binding energy is a major source of free energy used by enzymes to lower the activation energies of reactions. Enzymes are highly effective catalysts, commonly enhancing reaction rates by a factor of to . Enzyme-catalyzed reactions are characterized by the formation of a complex between substrate and enzyme (an ES complex). Substrate binding occurs in a pocket on the enzyme called the active site.
Enzymes are highly effective catalysts, commonly enhancing reaction rates by a factor of to . Enzyme-catalyzed reactions are characterized by the formation of a complex between substrate and enzyme (an ES complex). Substrate binding occurs in a pocket on the enzyme called the active site.