1.3 Physical Foundations
Living cells and organisms must perform work to stay alive and to reproduce themselves. The synthetic reactions that occur within cells, like the synthetic processes in any factory, require the input of energy. Energy input is also needed in the motion of a bacterium or an Olympic sprinter, in the flashing of a firefly or the electrical discharge of an eel. And the storage and expression of information require energy, without which structures that are rich in information inevitably become disordered and meaningless.
In the course of evolution, cells have developed highly efficient mechanisms for coupling the energy obtained from sunlight or chemical fuels to the many energy-requiring processes they must carry out. One goal of biochemistry is to understand, in quantitative and chemical terms, the means by which energy is extracted, stored, and channeled into useful work in living cells. We can consider cellular energy conversions — like all other energy conversions — in the context of the laws of thermodynamics. For a more extensive discussion of cellular thermodynamics, see Chapter 13.
Living Organisms Exist in a Dynamic Steady State, Never at Equilibrium with Their Surroundings
The molecules and ions contained within a living organism differ in kind and in concentration from those in the organism’s surroundings. A paramecium in a pond, a shark in the ocean, a bacterium in the soil, an apple tree in an orchard — all are different in composition from their surroundings and, once they have reached maturity, maintain a more or less constant composition in the face of a constantly changing environment.
Although the characteristic composition of an organism changes little through time, the population of molecules within the organism is far from static. Small molecules, macromolecules, and supramolecular complexes are continuously synthesized and broken down in chemical reactions that involve a constant flux of mass and energy through the system. The hemoglobin molecules carrying oxygen from your lungs to your brain at this moment were synthesized within the past month; by next month they will have been degraded and entirely replaced by new hemoglobin molecules. The glucose you ingested with your most recent meal is now circulating in your bloodstream; before the day is over these particular glucose molecules will have been converted into something else — carbon dioxide or fat, perhaps — and will have been replaced with a fresh supply of glucose, so that your blood glucose concentration is more or less constant over the whole day. The amounts of hemoglobin and glucose in the blood remain nearly constant because the rate of synthesis or intake of each just balances the rate of its breakdown, consumption, or conversion into some other product. The constancy of concentration is the result of a dynamic steady state, a steady state that is far from equilibrium. Maintaining this steady state requires the constant investment of energy; when a cell can no longer obtain energy, it dies and begins to decay toward equilibrium with its surroundings. We consider below exactly what is meant by “steady state” and “equilibrium.”
Organisms Transform Energy and Matter from Their Surroundings
For chemical reactions occurring in solution, we can define a system as all the constituent reactants and products, the solvent that contains them, and the immediate atmosphere — in short, everything within a defined region of space. The system and its surroundings together constitute the universe. If the system exchanges neither matter nor energy with its surroundings, it is said to be isolated. If the system exchanges energy but not matter with its surroundings, it is a closed system; if it exchanges both energy and matter with its surroundings, it is an open system.
A living organism is an open system; it exchanges both matter and energy with its surroundings. Organisms obtain energy from their surroundings in two ways: (1) they take up chemical fuels (such as glucose) from the environment and extract energy by oxidizing them (see Box 1-3, Case 2); or (2) they absorb energy from sunlight.
The first law of thermodynamics describes the principle of the conservation of energy: in any physical or chemical change, the total amount of energy in the universe remains constant, although the form of the energy may change. This means that while energy is “used” by a system, it is not “used up”; rather, it is converted from one form into another — from potential energy in chemical bonds, say, into kinetic energy of heat and motion. Cells are consummate transducers of energy, capable of interconverting chemical, electromagnetic, mechanical, and osmotic energy with great efficiency (Fig. 1-24).
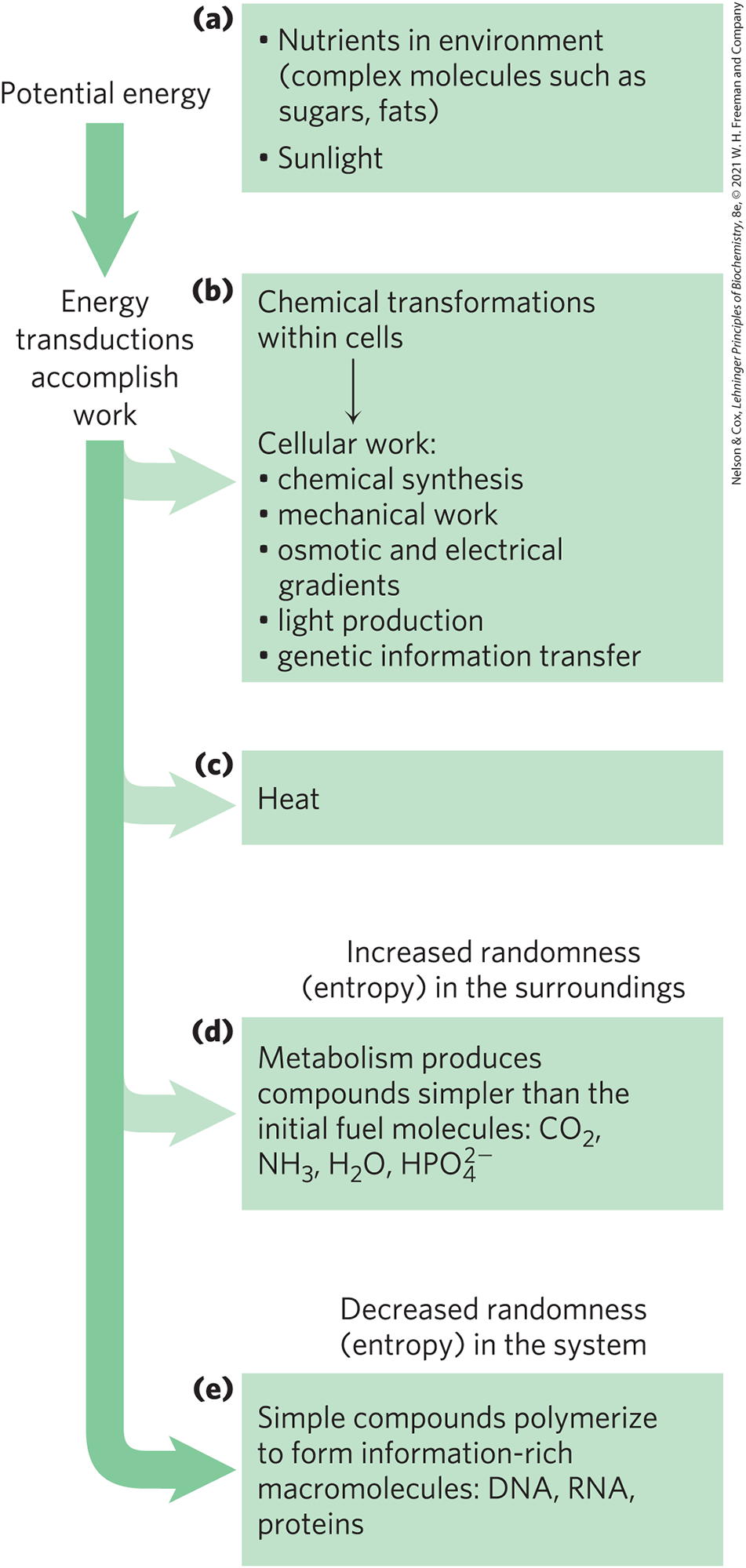
FIGURE 1-24 Some energy transformations in living organisms. As metabolic energy is spent to do cellular work, the randomness of the system plus surroundings (expressed quantitatively as entropy) increases as the potential energy of complex nutrient molecules decreases. (a) Living organisms extract energy from their surroundings; (b) convert some of it into useful forms of energy to produce work; (c) return some energy to the surroundings as heat; and (d) release end-product molecules that are less well organized than the starting fuel, increasing the entropy of the universe. One effect of all these transformations is (e) increased order (decreased randomness) in the system in the form of complex macromolecules.
The figure has five boxes stacked vertically at the left and labeled a through e. At the right are two arrows pointing down. Text above the short top arrow reads, potential energy. Next to box b, text beneath the short arrow reads, energy transductions accomplish work. A long arrow points down beneath this with arrow heads branching off to each box. The text in each box is as follows. a: nutrients in environment (complex molecules such as sugars, fats), sunlight. b: chemical transformations within cells, followed by an arrow that points down to cellular work, which includes chemical synthesis, mechanical work, osmotic and electrical gradients, light production, and genetic information transfer. c: heat. d: text above the box reads, increased randomness (entropy) in the surroundings. Text in the box reads, metabolism produces compounds simpler than the initial fuel molecules: C O 2, N H 3, H 2 O, H P O 4 superscript 2 minus. e: text above the box reads, decreased randomness (entropy) in the system. Text in the box reads, simple compounds polymerize to form information-rich macromolecules: D N A, R N A, proteins.
Nearly all living organisms derive their energy, directly or indirectly, from the radiant energy of sunlight. In the photoautotrophs, light-driven splitting of water during photosynthesis releases its electrons for the reduction of and the release of into the atmosphere:
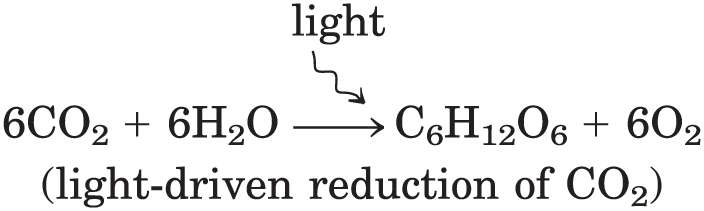
Nonphotosynthetic organisms (chemotrophs) obtain the energy they need by oxidizing the energy-rich products of photosynthesis stored in plants, then passing the electrons thus acquired to atmospheric to form water, and other end products, which are recycled in the environment:
Thus autotrophs and heterotrophs participate in global cycles of and driven ultimately by sunlight, making these two large groups of organisms interdependent. Virtually all energy transductions in cells can be traced to this flow of electrons from one molecule to another, in a “downhill” flow from higher to lower electrochemical potential; as such, this is formally analogous to the flow of electrons in a battery-driven electric circuit. All these reactions involved in electron flow are oxidation-reduction reactions: one reactant is oxidized (loses electrons) as another is reduced (gains electrons).
Creating and Maintaining Order Requires Work and Energy
As we’ve noted, DNA, RNA, and proteins are informational macromolecules; the precise sequence of their monomeric subunits contains information, just as the letters in this sentence do. In addition to using chemical energy to form the covalent bonds between these subunits, the cell must invest energy to order the subunits in their correct sequence. It is extremely improbable that amino acids in a mixture would spontaneously condense into a single type of protein, with a unique sequence. This would represent increased order in a population of molecules; but according to the second law of thermodynamics, the tendency in nature is toward ever-greater disorder in the universe: randomness in the universe is constantly increasing. To bring about the synthesis of macromolecules from their monomeric units, free energy must be supplied to the system (in this case, the cell). We discuss the quantitative energetics of oxidation-reduction reactions in Chapter 13.
The randomness or disorder of the components of a chemical system is expressed as entropy, S (Box 1-3). Any change in randomness of the system is expressed as entropy change, ΔS, which by convention has a positive value when randomness increases. J. Willard Gibbs, the scientist who developed the theory of energy changes during chemical reactions, showed that the free energy, G, of any closed system can be defined in terms of three quantities: enthalpy, H, or heat content, roughly reflecting the number and kinds of bonds; entropy, S; and the absolute temperature, T (in Kelvin). The definition of free energy is G = H − TS. When a chemical reaction occurs at constant temperature, the free-energy change, ΔG, is determined by the enthalpy change, ΔH, reflecting the kinds and numbers of chemical bonds and noncovalent interactions broken and formed, and the entropy change, ΔS, describing the change in the system’s randomness:
where, by definition, ΔH is negative for a reaction that releases heat, and ΔS is positive for a reaction that increases the system’s randomness.

J. Willard Gibbs, 1839–1903
A process tends to occur spontaneously only if ΔG is negative (if free energy is released in the process). Yet cell function depends largely on molecules, such as proteins and nucleic acids, for which the free energy of formation is positive: the molecules are less stable and more highly ordered than a mixture of their monomeric components. To carry out these thermodynamically unfavorable, energy-requiring (endergonic) reactions, cells couple them to other reactions that liberate free energy (exergonic reactions), so that the overall process is exergonic: the sum of the free-energy changes is negative. The exergonic reaction most commonly employed in this way involves adenosine triphosphate (ATP; Fig. 1-25) in which two phosphoanhydride bonds are capable of supplying the free energy to make a coupled endergonic reaction possible. In Section 13.3 we discuss in more detail this role of ATP.
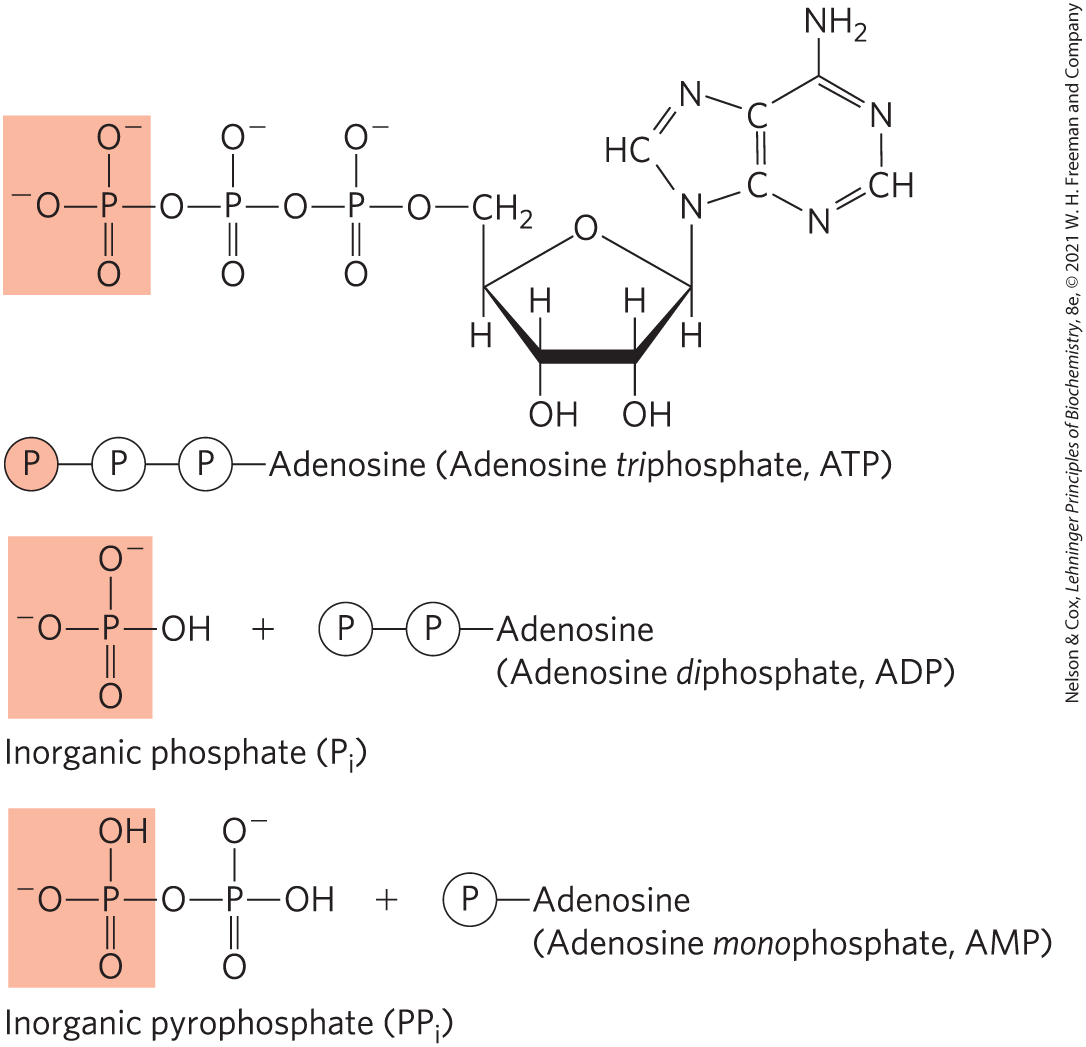
FIGURE 1-25 Adenosine triphosphate (ATP) provides energy. Here, each represents a phosphoryl group. The removal of the terminal phosphoryl group (shaded light red) of ATP, by breakage of a phosphoanhydride bond to generate adenosine diphosphate (ADP) and inorganic phosphate ion is highly exergonic, and this reaction is coupled to many endergonic reactions in the cell (as in the example in Worked Example 1-2). ATP also provides energy for many cellular processes by undergoing cleavage that releases the two terminal phosphates as inorganic pyrophosphate often abbreviated
The diagram shows three stages of the process from top to bottom. At the top, Adenosine triphosphate with tri italicized, A T P, is shown with a structural formula and as a chain of three circles labeled P with the left-hand P highlighted and adenosine bonded to the other side. The structural formula shows a five-membered ring with O at the top vertex, C 1 bonded to N of a five-membered ring fused with a six-membered ring, C 2 and C 3 bonded to H above and O H below, and C 4 bonded to H below and C H 2 above that is further bonded to O that is further bonded to P bonded to O minus above, double bonded to O below, and bonded to O that is further bonded to another P bonded to O minus above, double bonded to O below, and bonded to O on the left that is further bonded to a highlighted P that is bonded to two highlighted O minus and double bonded to highlighted O. The five-membered ring fused to a six-membered ring has N substituted to C at the bottom vertex, C H at the left vertex, N substituted for C at the top left vertex, a double bond at the top left side, and a double bond at the right side fused with the six-membered ring. The six-membered ring has N substituted for C at the top right vertex and bottom vertex, N H 2 bonded to the top vertex, and double bonds at the right top side and right bottom side. Beneath this, an inorganic phosphate (P i) is shown as the highlighted atoms from A T P with P bonded to O H plus a chain of two circles labeled P further bonded to adenosine (adenosine diphosphate with di italicized, A D P). Beneath this, inorganic pyrophosphate (P P i) is shown as the highlighted atoms with P bonded to O that is further bonded to P bonded to O minus above, bonded to O H to the right, and double bonded to O below plus a single circle labeled P bonded to adenosine (adenosine monophosphate with mono italicized, A M P).
Energy Coupling Links Reactions in Biology
The central issue in bioenergetics (the study of energy transformations in living systems) is the means by which energy from fuel metabolism or light capture is coupled to a cell’s energy-requiring reactions. With regard to energy coupling, it is useful to consider a simple mechanical example, as shown in Figure 1-26a. An object at the top of an inclined plane has a certain amount of potential energy as a result of its elevation. It tends to slide down the plane, losing its potential energy of position as it approaches the ground. When an appropriate string-and-pulley device couples the falling object to another, smaller object, the spontaneous downward motion of the larger can lift the smaller, accomplishing a certain amount of work. The amount of energy available to do work is the free-energy change, ΔG; this is always somewhat less than the theoretical amount of energy released, because some energy is dissipated as the heat of friction. The greater the elevation of the larger object, the greater the energy released (ΔG) as the object slides downward and the greater the amount of work that can be accomplished. The larger object can lift the smaller one only because, at the outset, the larger object was far from its equilibrium position: it had at some earlier point been elevated above the ground, in a process that itself required the input of energy.
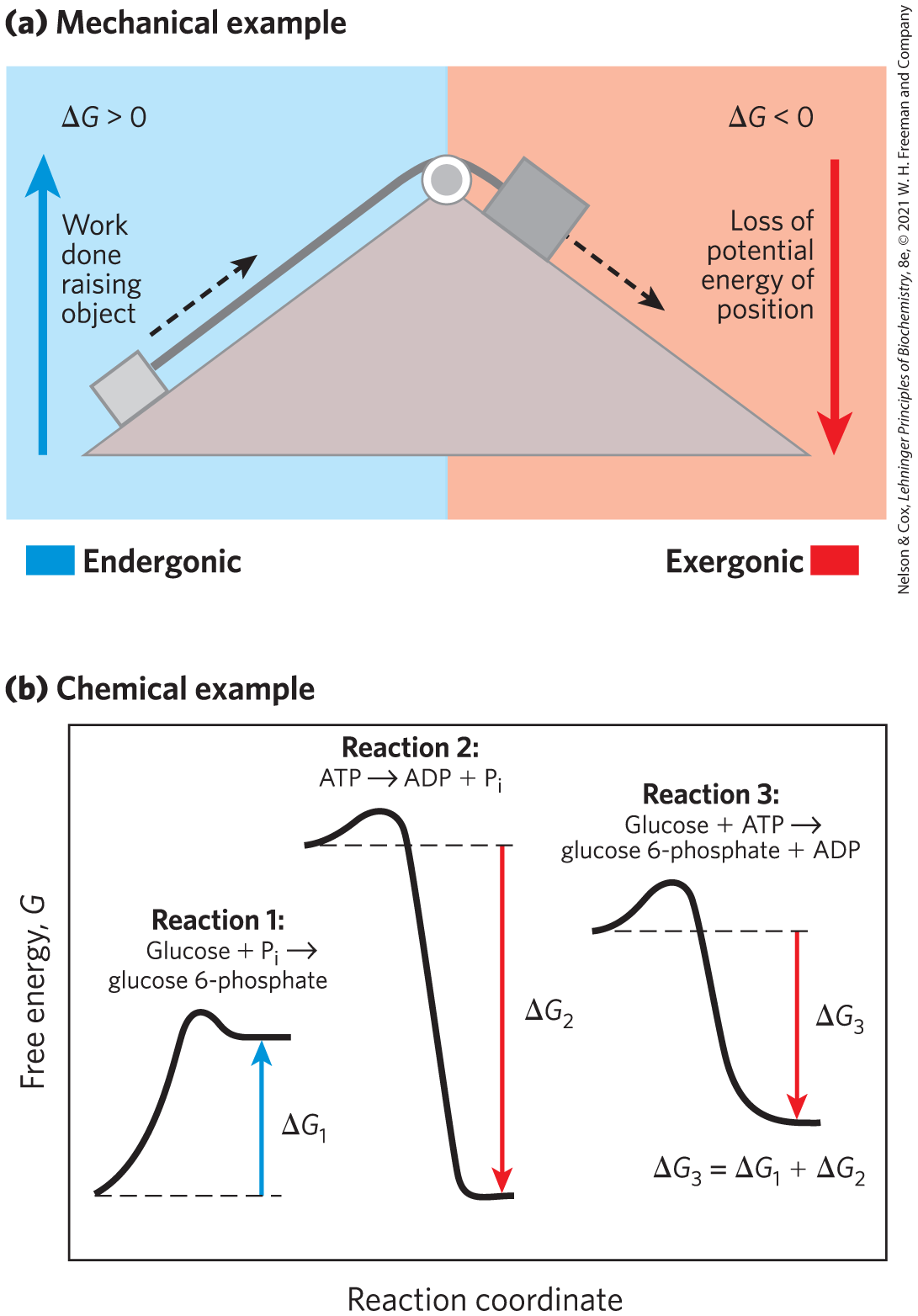
FIGURE 1-26 Energy coupling in mechanical and chemical processes. (a) The downward motion of an object releases potential energy that can do mechanical work. The potential energy made available by spontaneous downward motion, an exergonic process (red), can be coupled to the endergonic upward movement of another object (blue). (b) In reaction 1, the formation of glucose 6-phosphate from glucose and inorganic phosphate yields a product of higher energy than the two reactants. For this endergonic reaction, ΔG is positive. In reaction 2, the exergonic breakdown of adenosine triphosphate (ATP) has a large, negative free-energy change The third reaction is the sum of reactions 1 and 2, and the free-energy change, is the arithmetic sum of and Because is negative and relatively large, the overall reaction is exergonic and proceeds spontaneously.
Part a, at the top, shows a triangle with its vertex pointing up against a background that is divided in half vertically with different colors on either side of the vertex. A square accompanied by an arrow pointing toward the triangle vertex is shown against the left side of the triangle. A line runs from this square over the top of a circle at the vertex and slightly down the other side before reaching another square with an arrow pointing down from it along the right side of the triangle. On the left, an upward-pointing arrow is labeled, work done raising object and text reads, delta G is greater than 0. The left side is labeled Endergonic. On the right, a downward-pointing arrow is labeled, loss of potential energy of position and text reads, delta G is less than 0. The right side is labeled, Exergonic. Part b, at the bottom, shows a graph of three reactions. The graph plots reaction coordinate on the horizontal axis against free energy, G, on the vertical axis. No units are given. Reaction 1 is glucose plus P i yields glucose 6-phosphate and shows a horizontal dashed line across the bottom just above the horizontal axis with a curve that begins at the bottom left, curves rapidly upward to a point about halfway up the vertical axis, then curves down to form a rounded top before rapidly leveling off at a slightly lower level on the vertical axis. An arrow labeled, delta G 1 points upward from the dashed line to the flattened curve on the right side. Reaction 2 is A T P yields A D P plus P i. The curve begins at about three quarters of the height of the vertical axis, moves upward slightly, then curves downward all the way to the position where reaction 1 started before leveling off. A dashed horizontal line extends from the start of the curve. A downward arrow labeled, delta G 2 that is about double the length of the delta G 1 arrow points down from the dashed line to the end point. Reaction 3 is glucose plus A T P yields glucose 6-phosphate plus A D P. It has a similar shape to reaction 2, but begins at a slightly lower position on the vertical axis and ends at a slightly higher position on the vertical axis. A horizontal dashed line extends from its starting point and an arrow labeled, delta G 3, shorter than the arrow for delta G 2 and similar in length to the arrow for delta G 1, extends down to the end point. An equation underneath reads, delta G 3 equals delta G 1 plus delta G 2.
How does this apply in chemical reactions? In closed systems, chemical reactions proceed spontaneously until equilibrium is reached. When a system is at equilibrium, the rate of product formation exactly equals the rate at which product is converted to reactant. Thus there is no net change in the concentration of reactants and products. The energy change as the system moves from its initial state to equilibrium, with no changes in temperature or pressure, is given by the free-energy change, ΔG. The magnitude of ΔG depends on the particular chemical reaction and on how far from equilibrium the system is initially. Each compound involved in a chemical reaction contains a certain amount of potential energy, related to the kind and number of its bonds. In reactions that occur spontaneously, the products have less free energy than the reactants and thus the reaction releases free energy, which is then available to do work. Such reactions are exergonic; the decline in free energy from reactants to products is expressed as a negative value. Endergonic reactions require an input of energy, and their ΔG values are positive. This coupling of an exergonic reaction to an endergonic reaction is illustrated in Figure 1-26b. As in mechanical processes, only part of the energy released in exergonic chemical reactions can be used to accomplish work. In living systems, some energy is dissipated as heat or is lost to increasing entropy.
and Are Measures of a Reaction’s Tendency to Proceed Spontaneously
The tendency of a chemical reaction to go to completion can be expressed as an equilibrium constant. For the reaction in which a moles of A react with b moles of B to give c moles of C and d moles of D,
the equilibrium constant, is given by
where is the concentration of A, the concentration of B, and so on, when the system has reached equilibrium. is dimensionless (that is, has no units of measurement), but, as we explain on page 54, we will include molar units in our calculations to reinforce the point that molar concentrations (represented by the square brackets) must be used in the calculation of equilibrium constants. A large value of means the reaction tends to proceed until the reactants are almost completely converted into the products.
WORKED EXAMPLE 1-1 Are ATP and ADP at Equilibrium in Cells?
ATP breakdown yields adenosine diphosphate (ADP) and inorganic phosphate The equilibrium constant, for the reaction is :
If the measured cellular concentrations are [ATP] = 5 mm, [ADP] = 0.5 mm, and is this reaction at equilibrium in living cells?
SOLUTION:
The definition of the equilibrium constant for this reaction is
From the measured cellular concentrations given above, we can calculate the mass-action ratio, Q:
This value is far from the equilibrium constant for the reaction so the reaction is very far from equilibrium in cells. [ATP] is far higher, and [ADP] is far lower, than is expected at equilibrium. How can a cell hold its [ATP]/[ADP] ratio so far from equilibrium? It does so by continuously extracting energy (from nutrients such as glucose) and using it to make ATP from ADP and
Gibbs showed that ΔG (the actual free-energy change) for any chemical reaction is a function of the standard free-energy change, — a constant that is characteristic of each specific reaction — and a term that expresses the initial concentrations of reactants and products:
(1-1)
where is the initial concentration of A, and so forth; R is the gas constant; and T is the absolute temperature.
ΔG is a measure of the distance of a system from its equilibrium position. When a reaction has reached equilibrium, no driving force remains and it can do no work: ΔG = 0. For this special case, and so on, for all reactants and products, and
Substituting 0 for ΔG and for in Equation 1-1, we obtain the relationship
from which we see that is simply a second way (besides ) of expressing the driving force on a reaction. Because is experimentally measurable, we have a way of determining the thermodynamic constant characteristic of each reaction.
The units of and ΔG are joules per mole (or calories per mole). When is large and negative; when is large and positive. From a table of experimentally determined values of either or we can see at a glance which reactions tend to go to completion and which do not.
One caution about the interpretation of thermodynamic constants such as this show where the final equilibrium for a reaction lies but tell us nothing about how fast that equilibrium will be achieved. The rates of reactions are governed by the parameters of kinetics, a topic we consider in detail in Chapter 6.
In living organisms, just as in the mechanical example in Figure 1-26a, an exergonic reaction can be coupled to an endergonic reaction to drive otherwise unfavorable reactions. Figure 1-26b, a reaction coordinate diagram, illustrates this principle for the conversion of glucose to glucose 6-phosphate, the first step in the pathway for oxidation of glucose. The most direct way to produce glucose 6-phosphate would be
Reaction 1:
This reaction does not occur spontaneously; is positive. A second, highly exergonic reaction can occur in all cells:
Reaction 2:
These two chemical reactions share a common intermediate, which is consumed in reaction 1 and produced in reaction 2. The two reactions can therefore be coupled in the form of a third reaction, which we can write as the sum of reactions 1 and 2, with the common intermediate, omitted from both sides of the equation:
Reaction 3:
Because more energy is released in reaction 2 than is consumed in reaction 1, the free-energy change for reaction 3, is negative, and the synthesis of glucose 6-phosphate can therefore occur by reaction 3.
WORKED EXAMPLE 1-2 Standard Free-Energy Changes Are Additive
Given that the standard free-energy change for the reaction is 13.8 kJ/mol, and the standard free-energy change for the reaction is −30.5 kJ/mol, what is the free-energy change for the reaction glucose + ATP → glucose 6-phosphate + ADP?
SOLUTION:
We can write the equation for this reaction as the sum of two other reactions:
The standard free-energy change for two reactions that sum to a third is simply the sum of the two individual reactions. A negative value for indicates that the reaction will tend to occur spontaneously.
The coupling of exergonic and endergonic reactions through a shared intermediate is central to the energy exchanges in living systems. As we shall see, reactions that break down ATP (such as reaction 2 in Fig. 1-26b) release energy that drives many endergonic processes in cells. ATP breakdown in cells is exergonic because all living cells maintain a concentration of ATP far above its equilibrium concentration. It is this disequilibrium that allows ATP to serve as the major carrier of chemical energy in all cells. As we describe in detail in Chapter 13, it is not the mere breakdown of ATP that provides energy to drive endergonic reactions; rather, it is the transfer of a phosphoryl group from ATP to another small molecule (glucose in the case above) that conserves some of the chemical potential originally in ATP.
WORKED EXAMPLE 1-3 Energetic Cost of ATP Synthesis
If the equilibrium constant, for the reaction
is calculate the standard free-energy change, for the synthesis of ATP from ADP and at
SOLUTION:
First calculate for the reaction above:
This is the standard free-energy change for the breakdown of ATP to ADP and The standard free-energy change for the reverse of a reaction has the same absolute value but the opposite sign. The standard free-energy change for the reverse of the above reaction is therefore 30.5 kJ/mol. So, to synthesize 1 mol of ATP under standard conditions ( 1 m concentrations of ATP, ADP, and ), at least 30.5 kJ of energy must be supplied. The actual free-energy change in cells — approximately 50 kJ/mol — is greater than this because the concentrations of ATP, ADP, and in cells are not the standard 1 m (see Worked Example 13-2).
Enzymes Promote Sequences of Chemical Reactions
All biological macromolecules are much less thermodynamically stable than their monomeric subunits, yet they are kinetically stable: their uncatalyzed breakdown occurs so slowly (over years rather than seconds) that, on a time scale that matters for the organism, these molecules are stable. Virtually every chemical reaction in a cell occurs at a significant rate only because of the presence of enzymes — biocatalysts that, like all other catalysts, greatly enhance the rate of specific chemical reactions without being consumed in the process.
The path from reactant(s) to product(s) almost invariably involves an energy barrier, called the activation barrier (Fig. 1-27), that must be surmounted for any reaction to proceed. The breaking of existing bonds and formation of new ones generally requires, first, a distortion of the existing bonds to create a transition state of higher free energy than either the reactant or the product (see Section 6.2). The highest point in the reaction coordinate diagram represents the transition state, and the difference in energy between the reactant in its ground state and in its transition state is the activation energy, . An enzyme catalyzes a reaction by providing a more comfortable fit for the transition state: a surface that complements the transition state in stereochemistry, polarity, and charge. The binding of enzyme to the transition state is exergonic, and the energy released by this binding reduces the activation energy for the reaction and greatly increases the reaction rate.
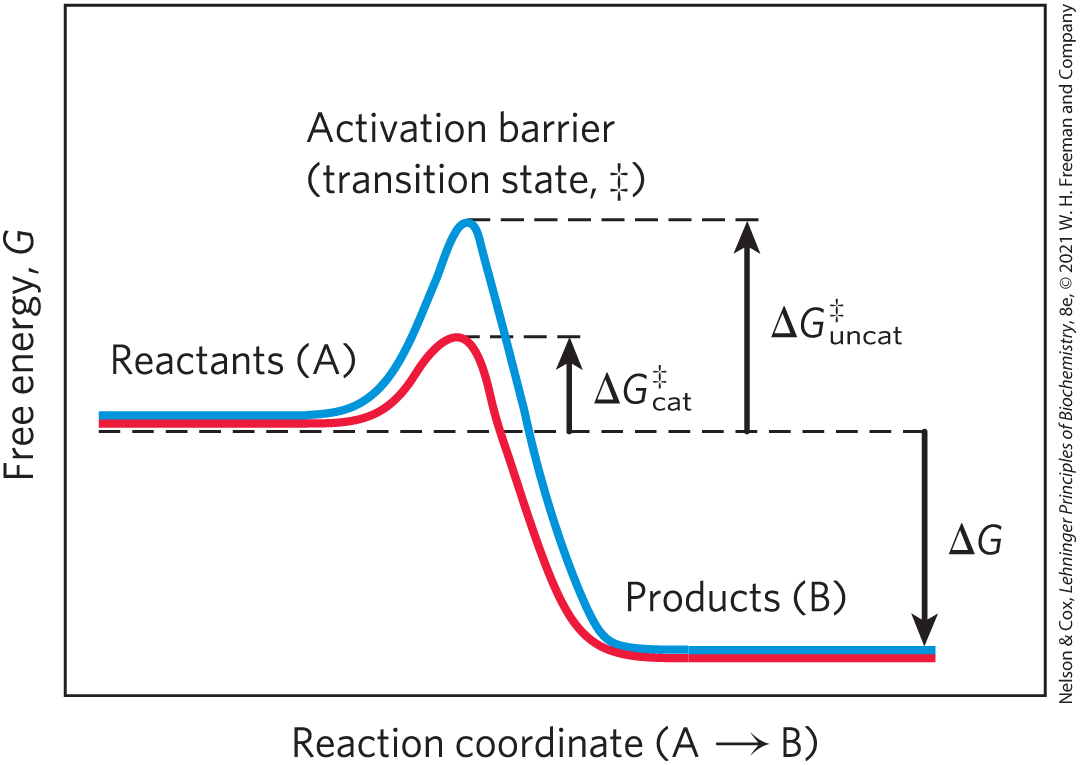
FIGURE 1-27 Energy changes during a chemical reaction. An activation barrier, representing the transition state, must be overcome in the conversion of reactants (A) into products (B), even though the products are more stable than the reactants, as indicated by a large, negative free-energy change (ΔG). The energy required to overcome the activation barrier is the activation energy Enzymes catalyze reactions by lowering the activation barrier. They bind the transition-state intermediates tightly, and the binding energy of this interaction effectively reduces the activation energy from (blue curve) to (red curve). (Note that activation energy is not related to free-energy change, ΔG.)
The graph plots reaction coordinate (A yielding B) on the horizontal axis against free energy, G on the vertical axis. A horizontal dotted line extends from just below half the height of the vertical axis. There are two curves shown. The left side of the dotted line, where both curves start, is labeled, reactants (A). The first curve runs along the horizontal line to about one-third the length of the horizontal axis, rises to a peak at about two-thirds the height of the vertical axis and half the length of the horizontal axis, and then drops sharply until it levels off under text reading products (B) just above the horizontal axis at just beyond half the length of the horizontal axis. Above the peak, text reads, activation barrier (transition state, double cross shape). An arrow labeled, delta G superscript double cross subscript uncat points upward from the dotted line to a horizontal line extending from the peak. The second curve is similar but has a much lower peak. A short arrow pointing up from the dotted line to a dotted line extending from the peak is labeled delta G superscript doublecross subscript cat. An arrow labeled, delta G points down from the dotted line to the end of both curves.
A further contribution to catalysis occurs when two or more reactants bind to the enzyme’s surface close to each other and with stereospecific orientations that favor their reaction. This increases by orders of magnitude the probability of productive collisions between reactants. As a result of these factors and several others, discussed in Chapter 6, many enzyme-catalyzed reactions proceed at rates times faster than the uncatalyzed reactions.
Cellular catalysts are, with some notable exceptions, proteins. (Some RNA molecules have enzymatic activity, as discussed in Chapters 26 and 27.) Again with a few exceptions, each enzyme catalyzes a specific reaction, and each reaction in a cell is catalyzed by a different enzyme. Thousands of different enzymes are therefore required by each cell. The multiplicity of enzymes, their specificity (the ability to discriminate between reactants), and their susceptibility to regulation give cells the capacity to lower activation barriers selectively. This selectivity is crucial for the effective regulation of cellular processes. By allowing specific reactions to proceed at significant rates at particular times, enzymes determine how matter and energy are channeled into cellular activities.
The thousands of enzyme-catalyzed chemical reactions in cells are functionally organized into many sequences of consecutive reactions, called pathways, in which the product of one reaction becomes the reactant in the next. Some pathways degrade organic nutrients into simple end products in order to extract chemical energy and convert it into a form useful to the cell; together, these degradative, free-energy-yielding reactions are designated catabolism. The energy released by catabolic reactions drives the synthesis of ATP. As a result, the cellular concentration of ATP is held far above its equilibrium concentration, so that ΔG for ATP breakdown is large and negative. Similarly, catabolism results in the production of the reduced electron carriers NADH (nicotinamide adenine dinucleotide) and NADPH (nicotinamide adenine dinucleotide phosphate hydrogen), both of which can donate electrons in processes that generate ATP or drive reductive steps in biosynthetic pathways. They are often referred to collectively as NAD(P)H.
Other pathways start with small precursor molecules and convert them to progressively larger and more complex molecules, including proteins and nucleic acids. Such synthetic pathways, which invariably require the input of energy, are collectively designated anabolism. The overall network of enzyme-catalyzed pathways, both catabolic and anabolic, constitutes cellular metabolism. ATP (as well as other energetically equivalent nucleoside triphosphates) is the connecting link between the catabolic and anabolic components of this network (shown schematically in Fig. 1-28). The pathways of enzyme-catalyzed reactions that act on the main constituents of cells — proteins, fats, sugars, and nucleic acids — are nearly identical in all living organisms. This remarkable unity of life is part of the evidence for a common evolutionary precursor for all living things.
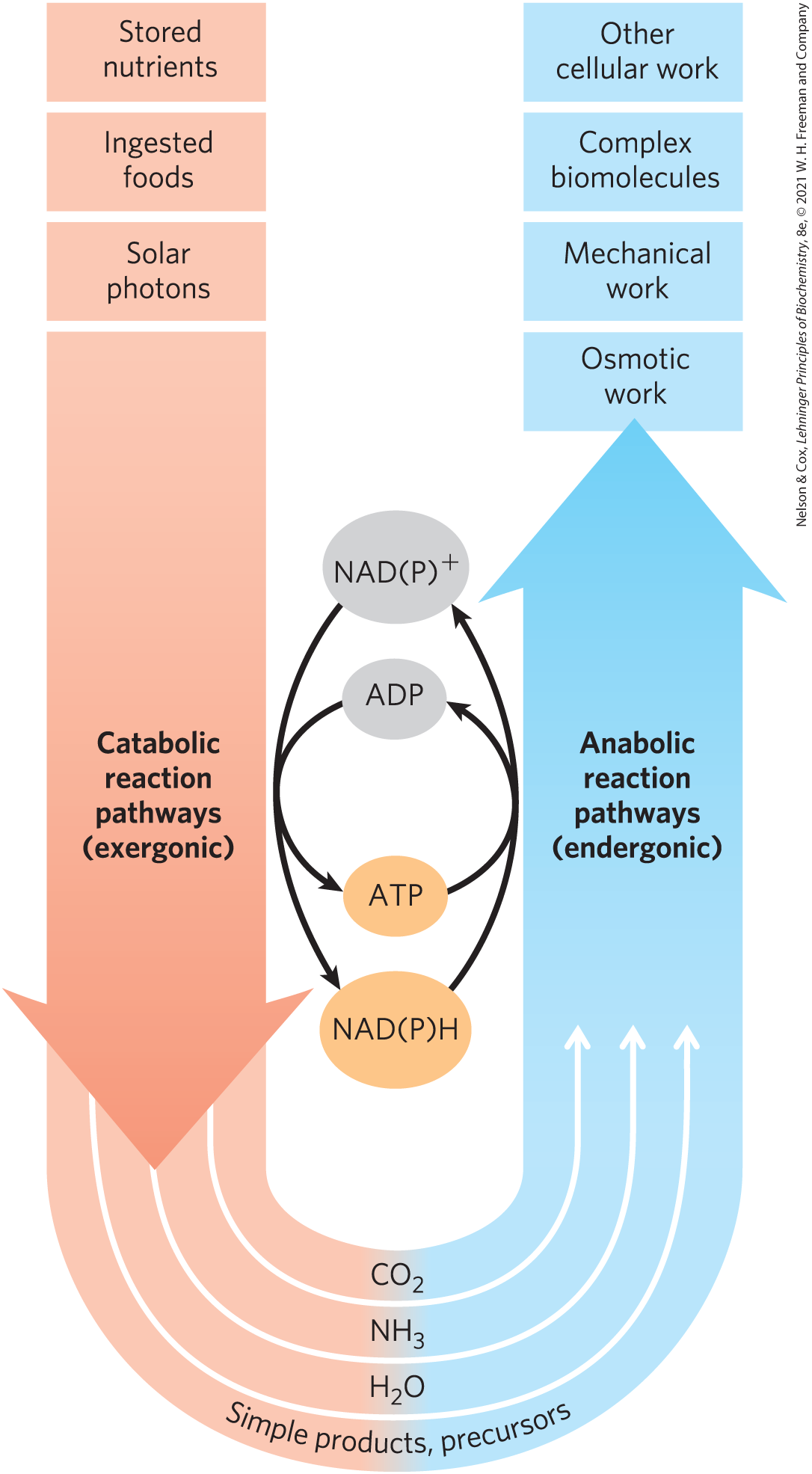
FIGURE 1-28 The central roles of ATP and NAD(P)H in metabolism. ATP is the shared chemical intermediate linking energy-releasing and energy-consuming cellular processes. Its role in the cell is analogous to that of money in an economy: it is “earned/produced” in exergonic reactions and “spent/consumed” in endergonic ones. NADH is an electron-carrying cofactor that collects electrons from oxidative reactions. The closely related NADPH carries electrons in a wide variety of reduction reactions in biosynthesis. Present in relatively low concentrations, these cofactors essential to anabolic reactions must be constantly regenerated by catabolic reactions.
Arrows form a U-shape that begins at the upper left and ends on the upper right. The arrow is broken into three rows at the upper left. From top to bottom, these are stored nutrients, ingested foods, and solar photons. A large arrow labeled catabolic reaction pathways (exergonic) points down to the lower left. A large arrow labeled anabolic reaction pathways (endergonic) points upward from the lower right. Four thin arrows connect these across the bottom of the U and are labeled C O 2; N H 3; H 2 O; and simple products, precursors. From top to bottom, four boxes in the upper right read other cellular work, complex biomolecules, mechanical work, and osmotic work. In the middle, between the big arrows on left and right, N A D (P) plus in an oval has an arrow pointing down along the catabolic reaction pathways arrow to N A D (P) H in an oval near the base of the U. Another arrow points upward along the anabolic reaction pathway arrow back to N A D (P) plus. Beneath the N A D (P) plus oval, a smaller oval labeled A D P has an arrow pointing down to an oval labeled A T P above N A D (P) H. Another arrow points up from A T P to A D P.
Metabolism Is Regulated to Achieve Balance and Economy
Not only do living cells simultaneously synthesize thousands of different kinds of carbohydrate, fat, protein, and nucleic acid molecules and their simpler subunits, but they do so in the precise proportions required by the cell under any given circumstance. For example, during rapid cell growth the precursors of proteins and nucleic acids must be made in large quantities, whereas in nongrowing cells the requirement for these precursors is much reduced. Key enzymes in each metabolic pathway are regulated so that each type of precursor molecule is produced in a quantity appropriate to the current requirements of the cell.
Consider the pathway in E. coli that leads to the synthesis of the amino acid isoleucine, a constituent of proteins. The pathway has five steps catalyzed by five different enzymes (A through F represent the intermediates in the pathway):
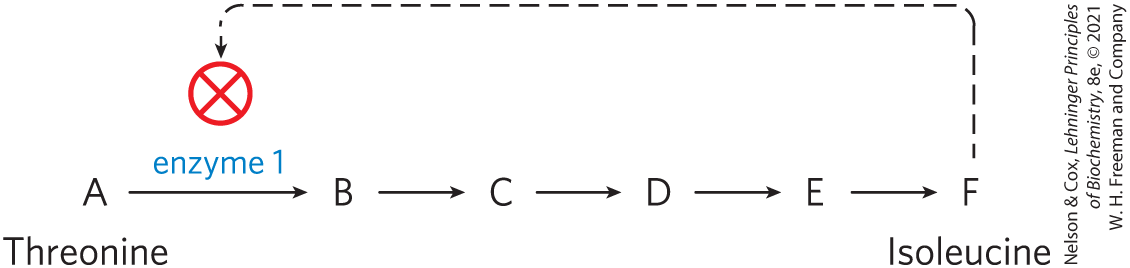
If a cell begins to produce more isoleucine than it needs for protein synthesis, the unused isoleucine accumulates, and the increased concentration inhibits the catalytic activity of the first enzyme in the pathway, immediately slowing the production of isoleucine. Such feedback inhibition keeps the production and utilization of each metabolic intermediate in balance. (Throughout the book, we use to indicate inhibition of an enzymatic reaction.)
Although the concept of discrete pathways is an important tool for organizing our understanding of metabolism, it is an oversimplification. There are thousands of metabolic intermediates in a cell, many of which are part of more than one pathway. Metabolism would be better represented as a web of interconnected and interdependent pathways. A change in the concentration of any one metabolite would start a ripple effect, influencing the flow of materials through other pathways. The task of understanding these complex interactions among intermediates and pathways in quantitative terms is daunting, but systems biology, discussed in Chapter 9, has begun to offer important insights into the overall regulation of metabolism.
Cells also regulate the synthesis of their own catalysts, the enzymes, in response to increased or diminished need for a metabolic product; this is the substance of Chapter 28. The regulated expression of genes (the translation from information in DNA to active protein in the cell) and the synthesis of enzymes are other layers of metabolic control in the cell. All layers must be taken into account when the overall control of cellular metabolism is described.
SUMMARY 1.3 Physical Foundations
- Living cells extract and channel energy to maintain themselves in a dynamic steady state distant from equilibrium.
- Living cells are open systems, exchanging matter and energy with their surroundings. Energy is obtained from sunlight or chemical fuels when the energy from electron flow is converted into the chemical bonds of ATP.
- The tendency for a chemical reaction to proceed toward equilibrium can be expressed as the free-energy change, ΔG. When ΔG of a reaction is negative, the reaction is exergonic and tends to go toward completion; when ΔG is positive, the reaction is endergonic and tends to go in the reverse direction. When two reactions can be summed to yield a third reaction, the ΔG for this overall reaction is the sum of the ΔG values for the two separate reactions.
- The reactions converting ATP to and ADP are highly exergonic (large negative ΔG). Many endergonic cellular reactions are driven by coupling them, through a common intermediate, to these highly exergonic reactions.
- The standard free-energy change for a reaction, is a physical constant that is related to the equilibrium constant by the equation
- Most cellular reactions proceed at useful rates only because enzymes are present to catalyze them. Enzymes act in part by stabilizing the transition state, reducing the activation energy, and increasing the reaction rate by many orders of magnitude. The catalytic activity of enzymes in cells is regulated.
- Metabolism is the sum of many interconnected reaction sequences that interconvert cellular metabolites. Each sequence is regulated to provide what the cell needs at a given time and to expend energy only when necessary.
 Nearly all living organisms derive their energy, directly or indirectly, from the radiant energy of sunlight. In the photoautotrophs, light-driven splitting of water during photosynthesis releases its electrons for the reduction of and the release of into the atmosphere:
Nearly all living organisms derive their energy, directly or indirectly, from the radiant energy of sunlight. In the photoautotrophs, light-driven splitting of water during photosynthesis releases its electrons for the reduction of and the release of into the atmosphere: represents a phosphoryl group. The removal of the terminal phosphoryl group (shaded light red) of ATP, by breakage of a phosphoanhydride bond to generate adenosine diphosphate (ADP) and inorganic phosphate ion is highly exergonic, and this reaction is coupled to many endergonic reactions in the cell (as in the example in
represents a phosphoryl group. The removal of the terminal phosphoryl group (shaded light red) of ATP, by breakage of a phosphoanhydride bond to generate adenosine diphosphate (ADP) and inorganic phosphate ion is highly exergonic, and this reaction is coupled to many endergonic reactions in the cell (as in the example in  The pathways of enzyme-catalyzed reactions that act on the main constituents of cells — proteins, fats, sugars, and nucleic acids — are nearly identical in all living organisms. This remarkable unity of life is part of the evidence for a common evolutionary precursor for all living things.
The pathways of enzyme-catalyzed reactions that act on the main constituents of cells — proteins, fats, sugars, and nucleic acids — are nearly identical in all living organisms. This remarkable unity of life is part of the evidence for a common evolutionary precursor for all living things. to indicate inhibition of an enzymatic reaction.)
to indicate inhibition of an enzymatic reaction.) Living cells extract and channel energy to maintain themselves in a dynamic steady state distant from equilibrium.
Living cells extract and channel energy to maintain themselves in a dynamic steady state distant from equilibrium.