2.2 Ionization of Water, Weak Acids, and Weak Bases in Chapter 2 Water, The Solvent Of Life

2.2 Ionization of Water, Weak Acids, and Weak Bases

Although many of the solvent properties of water can be explained in terms of the uncharged $mathml alt text198$ $upper H Subscript 2 Baseline upper O$ molecule, the small degree of ionization of water to hydrogen ions $mathml alt text199$ $left-parenthesis upper H Superscript plus Baseline right-parenthesis$ and hydroxide ions $mathml alt text200$ $left-parenthesis OH Superscript minus Baseline right-parenthesis$ must also be taken into account. Like all reversible reactions, the ionization of water can be described by an equilibrium constant. When weak acids are dissolved in water, they contribute $mathml alt text201$ $upper H Superscript plus$ by ionizing; weak bases consume $mathml alt text202$ $upper H Superscript plus$ by becoming protonated. These processes are also governed by equilibrium constants. The total hydrogen ion concentration from all sources is experimentally measurable and is expressed as the pH of the solution. To predict the state of ionization of solutes in water, we must take into account the relevant equilibrium constants for each ionization reaction. Therefore, we now turn to a brief discussion of the ionization of water and of weak acids and bases dissolved in water.

Pure Water Is Slightly Ionized

Water molecules have a slight tendency to undergo reversible ionization to yield a hydrogen ion (a proton) and a hydroxide ion, giving the equilibrium

H_{2} O ⇌ H^{+} + {OH}^{-}

$upper H Subscript 2 Baseline upper O right harpoon over left harpoon upper H Superscript plus Baseline plus OH Superscript minus$

(2-1)

Although we commonly show the dissociation product of water as $mathml alt text205$ $upper H Superscript plus$ , free protons do not exist in solution; hydrogen ions formed in water are immediately hydrated to form hydronium ions $mathml alt text206$ $left-parenthesis upper H Subscript 3 Baseline upper O Superscript plus Baseline right-parenthesis$ . Hydrogen bonding between water molecules makes the hydration of dissociating protons virtually instantaneous:

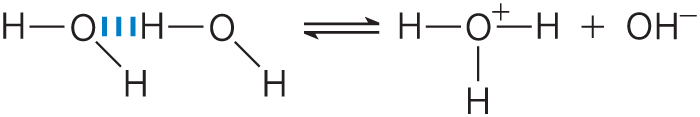
A Lewis diagram shows the interconversion of two water molecules with a hydronium ion and hydroxyl ion. Two water molecules are shown with O of the molecule on the left hydrogen bonded to H of the molecule on the right. After reacting, the products are a hydronium ion that has O plus in the center with three H around it and an O H minus.

The ionization of water can be measured by its electrical conductivity; pure water carries electrical current as $mathml alt text207$ $upper H Subscript 3 Baseline upper O Superscript plus$ migrates toward the cathode and $mathml alt text208$ $OH Superscript minus$ migrates toward the anode. The movement of hydronium and hydroxide ions in the electric field is extremely fast compared with that of other ions such as $mathml alt text209$ $Na Superscript plus$ , $mathml alt text210$ $upper K Superscript plus$ , and $mathml alt text211$ $Cl Superscript minus$ . This high ionic mobility results from the kind of “proton hopping” shown in Figure 2-13. No individual proton moves very far through the bulk solution, but a series of proton hops between hydrogen-bonded water molecules causes the net movement of a proton over a long distance in a remarkably short time. ( $mathml alt text212$ $OH Superscript minus$ also moves rapidly by proton hopping, but in the opposite direction.) As a result of the high ionic mobility of $mathml alt text213$ $upper H Superscript plus$ , acid-base reactions in aqueous solutions are exceptionally fast. As noted earlier, proton hopping very likely also plays a role in biological proton-transfer reactions (Fig. 2-10).

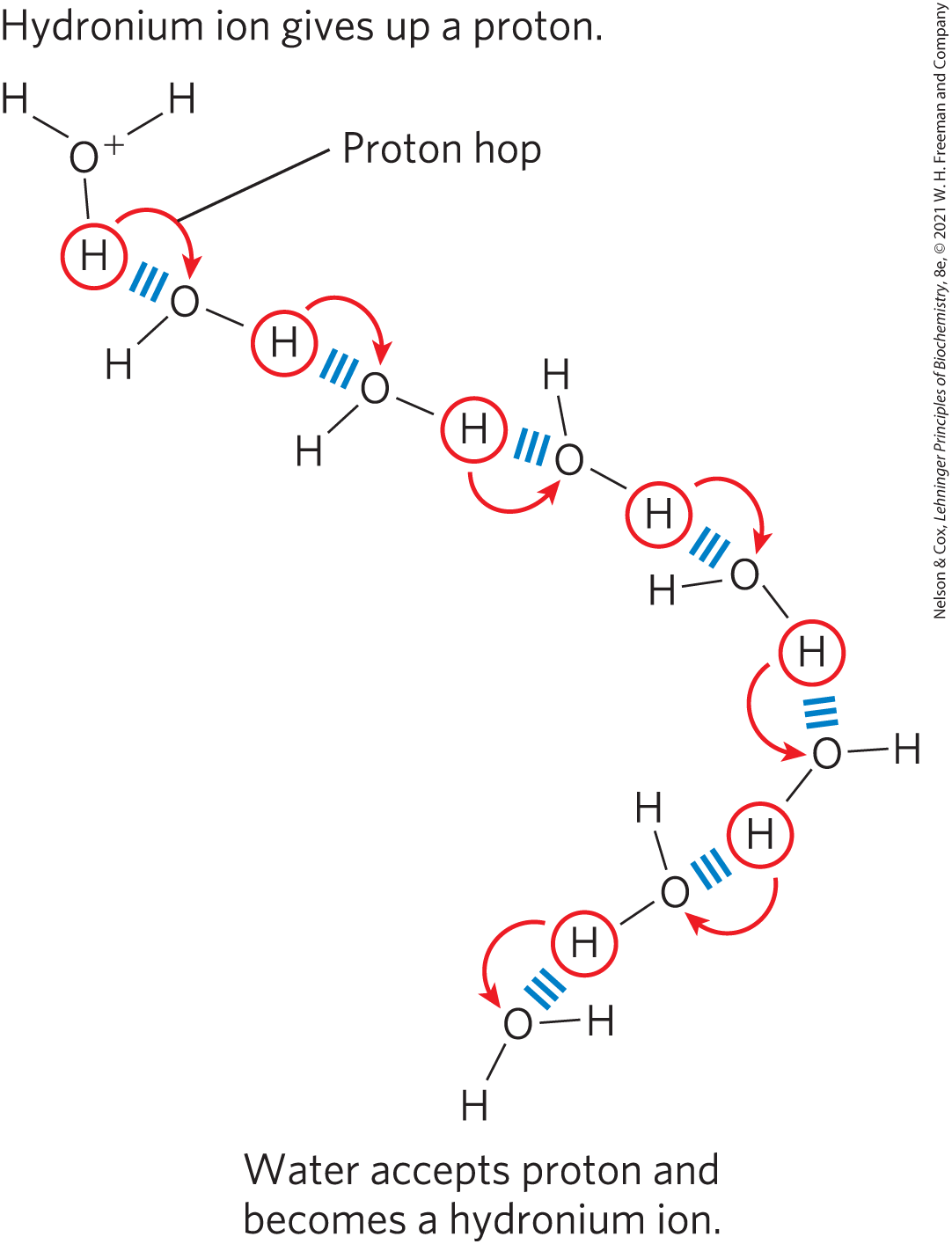
A figure shows how protons can move across a series of 8 water molecules as hydronium ions give up protons to become water molecules and water molecules accept protons to become hydronium ions. — FIGURE 2-13 Proton hopping. Short “hops” of protons between a series of hydrogen-bonded water molecules result in an extremely rapid net movement of a proton over a long distance. As a hydronium ion (upper left) gives up a proton, a water molecule some distance away (bottom) acquires one, becoming a hydronium ion. Proton hopping is much faster than true diffusion and explains the remarkably high ionic mobility of $mathml alt text214$ $upper H Superscript plus$ ions compared with other monovalent cations such as $mathml alt text215$ $Na Superscript plus$ and $mathml alt text216$ $upper K Superscript plus$ .

FIGURE 2-13 Proton hopping. Short “hops” of protons between a series of hydrogen-bonded water molecules result in an extremely rapid net movement of a proton over a long distance. As a hydronium ion (upper left) gives up a proton, a water molecule some distance away (bottom) acquires one, becoming a hydronium ion. Proton hopping is much faster than true diffusion and explains the remarkably high ionic mobility of $mathml alt text214$ $upper H Superscript plus$ ions compared with other monovalent cations such as $mathml alt text215$ $Na Superscript plus$ and $mathml alt text216$ $upper K Superscript plus$ .

Because reversible ionization is crucial to the role of water in cellular function, we must have a means of expressing the extent of ionization of water in quantitative terms. A brief review of some properties of reversible chemical reactions shows how this can be done.

The position of equilibrium of any chemical reaction is given by its equilibrium constant, $mathml alt text217$ $bold-italic upper K Subscript bold e q$ (sometimes expressed simply as K). For the generalized reaction

A + B ⇌ C + D

$upper A plus upper B right harpoon over left harpoon upper C plus upper D$

(2-2)

the equilibrium constant $mathml alt text220$ $upper K Subscript eq$ can be defined in terms of the concentrations of reactants (A and B) and products (C and D) at equilibrium:

K_{eq} = \frac{[C]_{eq} [D]_{eq}}{[A]_{eq} [B]_{eq}}

$upper K Subscript eq Baseline equals StartFraction left-bracket upper C right-bracket Subscript eq Baseline left-bracket upper D right-bracket Subscript eq Baseline Over left-bracket upper A right-bracket Subscript eq Baseline left-bracket upper B right-bracket Subscript eq Baseline EndFraction$

Strictly speaking, the concentration terms should be the activities, or effective concentrations in nonideal solutions, of each species. Except in very accurate work, however, the equilibrium constant may be approximated by measuring the concentrations at equilibrium. For reasons beyond the scope of this discussion, equilibrium constants are dimensionless. Nonetheless, we have generally retained the concentration units (m) in the equilibrium expressions used in this book to remind you that molarity is the unit of concentration used in calculating $mathml alt text222$ $upper K Subscript eq$ .

The equilibrium constant is fixed and characteristic for any given chemical reaction at a specified temperature. It defines the composition of the final equilibrium mixture, regardless of the starting amounts of reactants and products. Conversely, we can calculate the equilibrium constant for a given reaction at a given temperature if the equilibrium concentrations of all its reactants and products are known. As we showed in Chapter 1 (p. 24), the standard free-energy change $mathml alt text223$ $left-parenthesis upper Delta upper G degree right-parenthesis$ is directly related to ln $mathml alt text224$ $upper K Subscript eq$ .

The Ionization of Water Is Expressed by an Equilibrium Constant

The degree of ionization of water at equilibrium (Eqn 2-1) is small; at $mathml alt text225$ $25 degree upper C$ only about two of every $mathml alt text226$ $10 Superscript 9$ molecules in pure water are ionized at any instant. The equilibrium constant for the reversible ionization of water is

K_{eq} = \frac{[H^{+}] [{OH}^{-}]}{[H_{2} O]}

$upper K Subscript eq Baseline equals StartFraction left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket Over left-bracket upper H Subscript 2 Baseline upper O right-bracket EndFraction$

(2-3)

In pure water at $mathml alt text228$ $25 degree upper C$ , the concentration of water is 55.5 m—grams of $mathml alt text230$ $upper H Subscript 2 Baseline upper O$ in 1 L divided by its gram molecular weight: (1,000 g/L)/(18.015 g/mol)—and is essentially constant in relation to the very low concentrations of $mathml alt text233$ $upper H Superscript plus$ and $mathml alt text234$ $OH Superscript minus$ , namely $mathml alt text235$ $1 times 10 Superscript minus Superscript 7 Baseline upper M$ . Accordingly, we can substitute 55.5 m in the equilibrium constant expression (Eqn 2-3) to yield

K_{eq} = \frac{[H^{+}] [{OH}^{-}]}{[55.5 M]}

On rearranging, this becomes

(55.5 M) (K_{eq}) = [H^{+}] [{OH}^{-}] = K_{w}

$left-parenthesis 55.5 upper M right-parenthesis left-parenthesis upper K Subscript eq Baseline right-parenthesis equals left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket equals upper K Subscript w Baseline$

(2-4)

where $mathml alt text239$ $upper K Subscript w$ designates the product $mathml alt text240$ $left-parenthesis 55 .5 upper M right-parenthesis left-parenthesis upper K Subscript eq Baseline right-parenthesis$ , the ion product of water at $mathml alt text241$ $25 degree upper C$ .

The value for $mathml alt text242$ $upper K Subscript eq Baseline comma$ determined by electrical-conductivity measurements of pure water, is $mathml alt text243$ $1.8 times 10 Superscript minus Superscript 16 Baseline upper M$ at $mathml alt text244$ $25 degree upper C$ . Substituting this value for $mathml alt text245$ $upper K Subscript eq$ in Equation 2-4 gives the value of the ion product of water:

\begin{array}{l} K_{w} & = [H^{+}] [{OH}^{-}] = (55.5 M) (1.8 \times 10^{- 16} M) \\ = 1.0 \times 10^{- 14} M^{2} \end{array}

$StartLayout 1st Row 1st Column upper K Subscript w Baseline 2nd Column equals left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket equals left-parenthesis 55.5 upper M right-parenthesis left-parenthesis 1.8 times 10 Superscript negative 16 Baseline upper M right-parenthesis 2nd Row 1st Column Blank 2nd Column equals 1.0 times 10 Superscript negative 14 Baseline upper M squared EndLayout$

Thus the product $mathml alt text247$ $left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket$ in aqueous solutions at $mathml alt text248$ $25 degree upper C$ always equals $mathml alt text249$ $1 times 10 Superscript minus Superscript 14 Baseline upper M Superscript 2$ . When there are exactly equal concentrations of $mathml alt text250$ $upper H Superscript plus$ and $mathml alt text251$ $OH Superscript minus$ , as in pure water, the solution is said to be at neutral pH. At this pH, the concentrations of $mathml alt text254$ $upper H Superscript plus$ and $mathml alt text255$ $OH Superscript minus$ can be calculated from the ion product of water as follows:

K_{w} = [H^{+}] [{OH}^{-}] = {[H^{+}]}^{2} = {[{OH}^{-}]}^{2}

$upper K Subscript w Baseline equals left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket equals left-bracket upper H Superscript plus Baseline right-bracket squared equals left-bracket OH Superscript minus Baseline right-bracket squared$

Solving for $mathml alt text257$ $left-bracket upper H Superscript plus Baseline right-bracket$ gives

\begin{array}{l} [H^{+}] & = \sqrt{K_{w}} = \sqrt{1 \times 10^{- 14} M^{2}} \\ [H^{+}] & = [{OH}^{-}] = 10^{- 7} M \end{array}

$StartLayout 1st Row 1st Column left-bracket upper H Superscript plus Baseline right-bracket 2nd Column equals StartRoot upper K Subscript w Baseline EndRoot equals StartRoot 1 times 10 Superscript negative 14 Baseline upper M squared EndRoot 2nd Row 1st Column left-bracket upper H Superscript plus Baseline right-bracket 2nd Column equals left-bracket OH Superscript minus Baseline right-bracket equals 10 Superscript negative 7 Baseline upper M EndLayout$

As the ion product of water is constant, whenever $mathml alt text259$ $left-bracket upper H Superscript plus Baseline right-bracket$ is greater than $mathml alt text260$ $1 times 10 Superscript minus Superscript 7 Baseline upper M comma left-bracket OH Superscript minus Baseline right-bracket$ must be less than $mathml alt text261$ $1 times 10 Superscript negative 7 Baseline upper M$ , and vice versa. When $mathml alt text262$ $left-bracket upper H Superscript plus Baseline right-bracket$ is very high, as in a solution of hydrochloric acid, $mathml alt text263$ $left-bracket OH Superscript minus Baseline right-bracket$ must be very low. From the ion product of water, we can calculate $mathml alt text264$ $left-bracket upper H Superscript plus Baseline right-bracket$ if we know $mathml alt text265$ $left-bracket OH Superscript minus Baseline right-bracket$ , and vice versa.

WORKED EXAMPLE 2-2 Calculation of $mathml alt text266$ $left-bracket upper H Superscript bold-italic plus Baseline right-bracket$

What is the concentration of $mathml alt text267$ $upper H Superscript plus$ in a solution of 0.1 m NaOH? Because NaOH is a strong base, it dissociates completely into $mathml alt text270$ $Na Superscript plus$ and $mathml alt text271$ $OH Superscript minus$ .

SOLUTION:

We begin with the equation for the ion product of water:

K_{w} = [H^{+}] [{OH}^{-}]

$upper K Subscript w Baseline equals left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket$

With $mathml alt text273$ $left-bracket OH Superscript minus Baseline right-bracket equals 0 .1 upper M$ , solving for $mathml alt text274$ $left-bracket upper H Superscript plus Baseline right-bracket$ gives

\begin{array}{l} [H^{+}] & = \frac{K_{w}}{[{OH}^{-}]} = \frac{1 \times 10^{- 14} M^{2}}{0.1 M} = \frac{10^{- 14} M^{2}}{10^{- 1} M} \\ = 10^{- 13} M \end{array}

$StartLayout 1st Row 1st Column left-bracket upper H Superscript plus Baseline right-bracket 2nd Column equals StartFraction upper K Subscript w Baseline Over left-bracket OH Superscript minus Baseline right-bracket EndFraction equals StartFraction 1 times 10 Superscript negative 14 Baseline upper M squared Over 0.1 upper M EndFraction equals StartFraction 10 Superscript negative 14 Baseline upper M squared Over 10 Superscript negative 1 Baseline upper M EndFraction 2nd Row 1st Column Blank 2nd Column equals 10 Superscript negative 13 Baseline upper M EndLayout$

WORKED EXAMPLE 2-3 Calculation of $mathml alt text276$ $left-bracket bold-italic upper O bold-italic upper H Superscript bold-italic minus Baseline right-bracket$

What is the concentration of $mathml alt text277$ $OH Superscript minus$ in a solution with an $mathml alt text278$ $upper H Superscript plus$ concentration of $mathml alt text279$ $1.3 times 10 Superscript minus Superscript 4 Baseline upper M question-mark$

SOLUTION:

We begin with the equation for the ion product of water:

K_{w} = [H^{+}] [{OH}^{-}]

$upper K Subscript w Baseline equals left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket$

With $mathml alt text281$ $left-bracket upper H Superscript plus Baseline right-bracket equals 1.3 times 10 Superscript negative 4 Baseline upper M$ , solving for $mathml alt text282$ $left-bracket OH Superscript minus Baseline right-bracket$ gives

[{OH}^{-}] = \frac{K_{w}}{[H^{+}]} = \frac{1 \times 10^{- 14} M^{2}}{1.3 \times 10^{- 4} M} = 7.7 \times 10^{- 11} M

$left-bracket OH Superscript minus Baseline right-bracket equals StartFraction upper K Subscript w Baseline Over left-bracket upper H Superscript plus Baseline right-bracket EndFraction equals StartFraction 1 times 10 Superscript negative 14 Baseline upper M squared Over 1.3 times 10 Superscript negative 4 Baseline upper M EndFraction equals 7.7 times 10 Superscript negative 11 Baseline upper M$

In all calculations, be sure to round your answer to the correct number of significant figures, as here.

The pH Scale Designates the $mathml alt text285$ $bold upper H Superscript bold plus$ and $mathml alt text286$ $bold OH Superscript bold en-dash$ Concentrations

The ion product of water, $mathml alt text287$ $upper K Subscript w$ , is the basis for the pH scale (Table 2-5). It is a convenient means of designating the concentration of $mathml alt text289$ $upper H Superscript plus$ (and thus of $mathml alt text290$ $OH Superscript minus$ ) in any aqueous solution in the range between $mathml alt text291$ $1.0 upper M upper H Superscript plus$ and $mathml alt text292$ $1.0 upper M OH Superscript minus$ . The symbol p denotes “negative logarithm of.” The term pH is defined by the expression

pH = \log \frac{1}{[H^{+}]} = - \log [H^{+}]

$pH equals log StartFraction 1 Over left-bracket upper H Superscript plus Baseline right-bracket EndFraction equals minus log left-bracket upper H Superscript plus Baseline right-bracket$

TABLE 2-5 The pH Scale
$mathml alt text295$ $left-bracket bold upper H Superscript plus Baseline right-bracket left-parenthesis bold upper M right-parenthesis$	pH	$mathml alt text297$ $left-bracket bold upper O bold upper H Superscript minus Baseline right-bracket left-parenthesis bold upper M right-parenthesis$	pOH^a
$mathml alt text299$ $10 Superscript 0 Baseline left-parenthesis 1 right-parenthesis$	0	$mathml alt text301$ $10 Superscript negative 14$	14
$mathml alt text303$ $10 Superscript negative 1$	1	$mathml alt text305$ $10 Superscript negative 13$	13
$mathml alt text307$ $10 Superscript negative 2$	2	$mathml alt text309$ $10 Superscript negative 12$	12
$mathml alt text311$ $10 Superscript negative 3$	3	$mathml alt text313$ $10 Superscript negative 11$	11
$mathml alt text315$ $10 Superscript negative 4$	4	$mathml alt text317$ $10 Superscript negative 10$	10
$mathml alt text319$ $10 Superscript negative 5$	5	$mathml alt text321$ $10 Superscript negative 9$	9
$mathml alt text323$ $10 Superscript negative 6$	6	$mathml alt text325$ $10 Superscript negative 8$	8
$mathml alt text327$ $10 Superscript negative 7$	7	$mathml alt text329$ $10 Superscript negative 7$	7
$mathml alt text331$ $10 Superscript negative 8$	8	$mathml alt text333$ $10 Superscript negative 6$	6
$mathml alt text335$ $10 Superscript negative 9$	9	$mathml alt text337$ $10 Superscript negative 5$	5
$mathml alt text339$ $10 Superscript negative 10$	10	$mathml alt text341$ $10 Superscript negative 4$	4
$mathml alt text343$ $10 Superscript negative 11$	11	$mathml alt text345$ $10 Superscript negative 3$	3
$mathml alt text347$ $10 Superscript negative 12$	12	$mathml alt text349$ $10 Superscript negative 2$	2
$mathml alt text351$ $10 Superscript negative 13$	13	$mathml alt text353$ $10 Superscript negative 1$	1
$mathml alt text355$ $10 Superscript negative 14$	14	$mathml alt text357$ $10 Superscript 0 Baseline left-parenthesis 1 right-parenthesis$	0
^aThe expression pOH is sometimes used to describe the basicity, or $mathml alt text360$ $OH Superscript minus$ concentration, of a solution; pOH is defined by the expression $mathml alt text361$ $pOH equals minus log left-bracket OH Superscript minus Baseline right-bracket$ , which is analogous to the expression for pH. Note that in all cases, pH + pOH = 14.

For a precisely neutral solution at $mathml alt text364$ $25 degree upper C$ , in which the concentration of hydrogen ions is $mathml alt text365$ $1.0 times 10 Superscript negative 7 Baseline upper M$ , the pH can be calculated as follows:

pH = \log \frac{1}{1.0 \times 10^{- 7}} = 7.0

$pH equals log StartFraction 1 Over 1.0 times 10 Superscript negative 7 Baseline EndFraction equals 7.0$

Note that the concentration of $mathml alt text368$ $upper H Superscript plus$ must be expressed in molar (m) terms.

The value of 7 for the pH of a precisely neutral solution is not an arbitrarily chosen figure; it is derived from the absolute value of the ion product of water at $mathml alt text370$ $25 degree upper C$ , which by convenient coincidence is a round number. Solutions having a pH greater than 7 are alkaline or basic; the concentration of $mathml alt text372$ $OH Superscript minus$ is greater than that of $mathml alt text373$ $upper H Superscript plus$ . Conversely, solutions having a pH less than 7 are acidic.

Keep in mind that the pH scale is logarithmic, not arithmetic. To say that two solutions differ in pH by 1 pH unit means that one solution has ten times the $mathml alt text378$ $upper H Superscript plus$ concentration of the other, but it does not tell us the absolute magnitude of the difference. Figure 2-14 gives the pH values of some common aqueous fluids. A cola drink (pH 3.0) or red wine (pH 3.7) has an $mathml alt text382$ $upper H Superscript plus$ concentration approximately 10,000 times that of blood (pH 7.4).

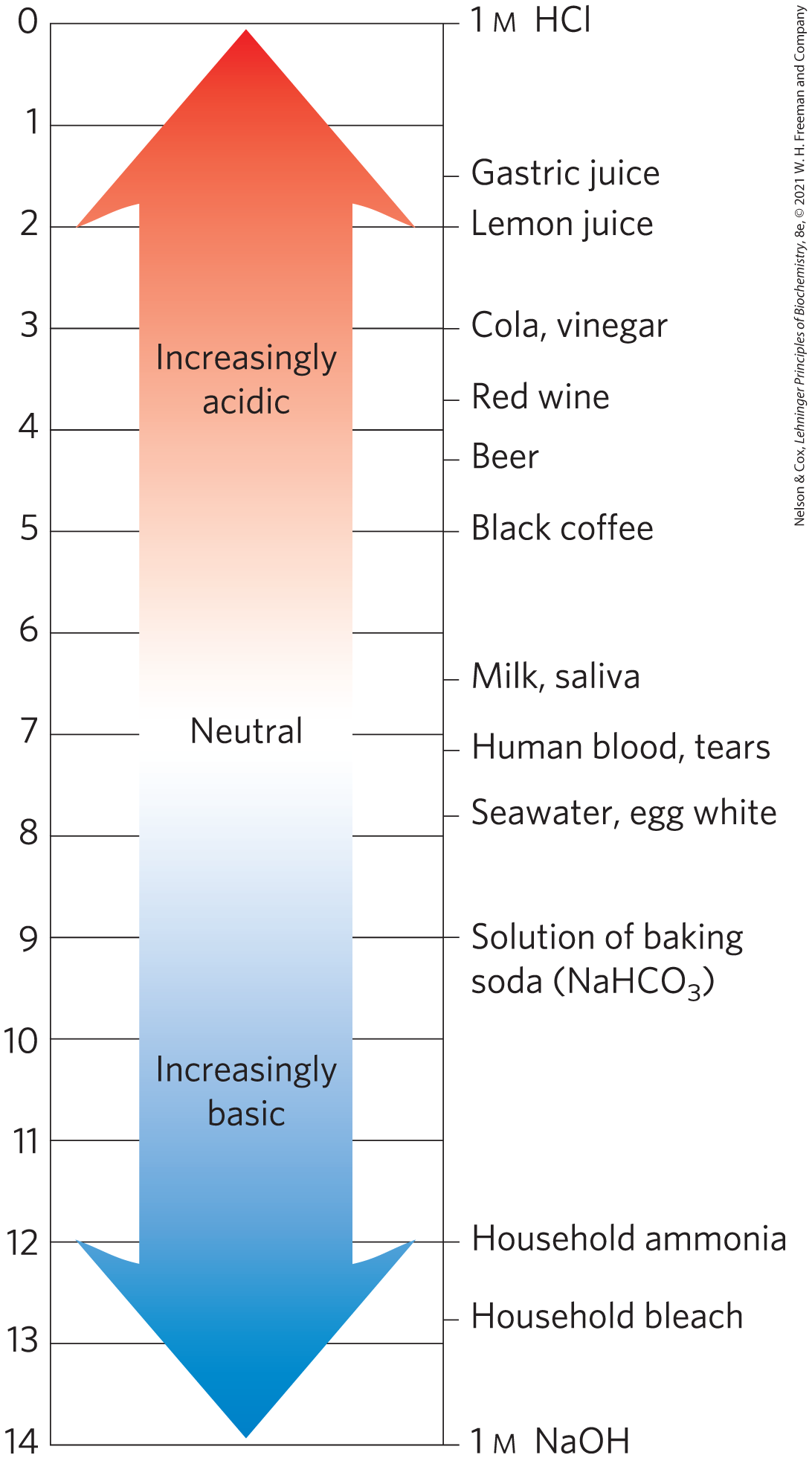
A drawing of a p H scale shows the p H of some aqueous fluids ranging from 1 M H C l at a p H of 0 to 1 M N a O H at a p H of 14. — FIGURE 2-14 The pH of some aqueous fluids.

Accurate determinations of pH in the chemical or clinical laboratory are made with a glass electrode that is selectively sensitive to $mathml alt text386$ $upper H Superscript plus$ concentration but insensitive to $mathml alt text387$ $Na Superscript plus$ , $mathml alt text388$ $upper K Superscript plus$ , and other cations. In a pH meter, the signal from the glass electrode placed in a test solution is amplified and compared with the signal generated by a solution of accurately known pH.

Measurement of pH is one of the most important and frequently used procedures in biochemistry. The pH affects the structure and activity of biological macromolecules, so a small change in pH can cause a large change in the structure and function of a protein. Measurements of the pH of blood and urine are commonly used in medical diagnoses. The pH of the blood plasma of people with severe, uncontrolled diabetes, for example, is often below the normal value of 7.4; this condition is called acidosis (described in more detail below). In certain other diseases the pH of the blood is higher than normal, a condition known as alkalosis. Extreme acidosis or alkalosis can be life-threatening (see Box 2-1).

Box 2-1 MEDICINE

On Being One’s Own Rabbit (Don’t Try This at Home!)

I wanted to find out what happened to a man when one made him more acid or more alkaline … One might, of course, have tried experiments on a rabbit first, and some work had been done along these lines; but it is difficult to be sure how a rabbit feels at any time. Indeed, some rabbits make no serious attempt to cooperate with one.

—J. B. S. Haldane, Possible Worlds, 1928

A century ago, physiologist and geneticist J. B. S. Haldane and his colleague H. W. Davies decided to experiment on themselves, to study how the body controls blood pH. They made themselves alkaline by hyperventilating and ingesting sodium bicarbonate, which left them panting and with violent headaches. They tried to acidify themselves by drinking hydrochloric acid, but calculated that it would take a gallon and a half of dilute HCl to get the desired effect, and a pint was enough to dissolve their teeth and burn their throats. Finally, it occurred to Haldane that if he ate ammonium chloride, it would break down in the body to release hydrochloric acid and ammonia. The ammonia would be converted to harmless urea in the liver (this process is described in detail in Fig. 18-10). The hydrochloric acid would combine with the sodium bicarbonate present in all tissues, producing sodium chloride and carbon dioxide. In this experiment, the resulting shortness of breath mimicked that in diabetic acidosis or end-stage kidney disease.

Meanwhile, Ernst Freudenberg and Paul György, pediatricians in Heidelberg, were studying tetany—muscle contractions occurring in the hands, arms, feet, and larynx—in infants. They knew that tetany was sometimes seen in patients who had lost large amounts of hydrochloric acid by constant vomiting, and they reasoned that if tissue alkalinity produced tetany, acidity might be expected to cure it. The moment they read Haldane’s paper on the effects of ammonium chloride, they tried giving ammonium chloride to babies with tetany, and they were delighted to find that the tetany cleared up in a few hours. This treatment didn’t remove the primary cause of the tetany, but it did give the infant and the physician time to deal with that cause.

Weak Acids and Bases Have Characteristic Acid Dissociation Constants

Hydrochloric, sulfuric, and nitric acids, commonly called strong acids, are completely ionized in dilute aqueous solutions; the strong bases NaOH and KOH are also completely ionized. Of more interest to biochemists is the behavior of weak acids and bases—those not completely ionized when dissolved in water. These are ubiquitous in biological systems and play important roles in metabolism and its regulation. The behavior of aqueous solutions of weak acids and bases is best understood if we first define some terms.

Acids (in the Brønsted-Lowry definition) are proton donors, and bases are proton acceptors. When a proton donor such as acetic acid $mathml alt text401$ $left-parenthesis CH Subscript 3 Baseline COOH right-parenthesis$ loses a proton, it becomes the corresponding proton acceptor, in this case the acetate anion $mathml alt text402$ $left-parenthesis CH Subscript 3 Baseline COO Superscript minus Baseline right-parenthesis$ . A proton donor and its corresponding proton acceptor make up a conjugate acid-base pair (Fig. 2-15), related by the reversible reaction

{CH}_{3} COOH ⇌ {CH}_{3} {COO}^{-} + H^{+}

$CH Subscript 3 Baseline COOH right harpoon over left harpoon CH Subscript 3 Baseline COO Superscript minus Baseline plus upper H Superscript plus$

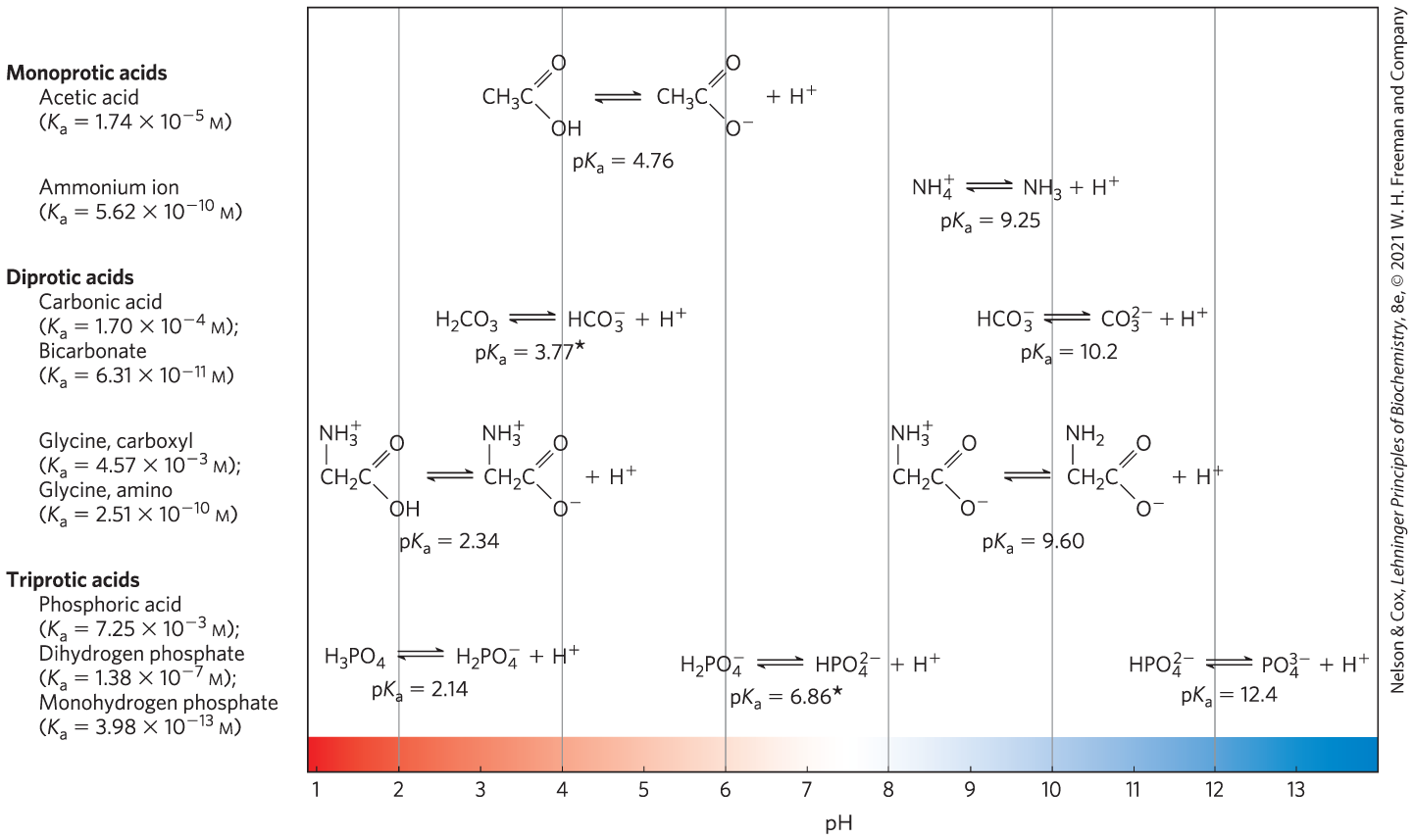
A figure uses Lewis structures to show examples of 9 conjugate acid-base pairs along a pH scale, including monoprotic, diprotic, and triprotic acids. — FIGURE 2-15 Conjugate acid-base pairs consist of a proton donor and a proton acceptor. Some compounds, such as acetic acid and ammonium ion, are monoprotic: they can give up only one proton. Others are diprotic (carbonic acid and glycine) or triprotic (phosphoric acid). The dissociation reactions for each pair are shown where they occur along a pH gradient. The equilibrium or dissociation constant (K) and its negative logarithm, the $mathml alt text405$ $p upper K Subscript a Baseline$ , are shown for each reaction. *For an explanation of apparent discrepancies in $mathml alt text406$ $p upper K Subscript a Baseline$ values for carbonic acid $mathml alt text407$ $left-parenthesis upper H Subscript 2 Baseline CO Subscript 3 Baseline right-parenthesis$ , see p. 63; and for dihydrogen phosphate $mathml alt text407a$ $left-parenthesis upper H Subscript 2 Baseline PO Subscript 4 Superscript minus Baseline right-parenthesis$ , see p. 58.

FIGURE 2-15 Conjugate acid-base pairs consist of a proton donor and a proton acceptor. Some compounds, such as acetic acid and ammonium ion, are monoprotic: they can give up only one proton. Others are diprotic (carbonic acid and glycine) or triprotic (phosphoric acid). The dissociation reactions for each pair are shown where they occur along a pH gradient. The equilibrium or dissociation constant (K) and its negative logarithm, the $mathml alt text405$ $p upper K Subscript a Baseline$ , are shown for each reaction. *For an explanation of apparent discrepancies in $mathml alt text406$ $p upper K Subscript a Baseline$ values for carbonic acid $mathml alt text407$ $left-parenthesis upper H Subscript 2 Baseline CO Subscript 3 Baseline right-parenthesis$ , see p. 63; and for dihydrogen phosphate $mathml alt text407a$ $left-parenthesis upper H Subscript 2 Baseline PO Subscript 4 Superscript minus Baseline right-parenthesis$ , see p. 58.

The figure shows a p H scale on the horizontal axis, ranging from 1 to 13, labeled in increments of 1. On the left, a list of acids and their K subscript are given as follows. Each is lined up horizontally with its reaction above the p H scale. Monoprotic acids include acetic acid (K subscript a equals 1.74 x 10 superscript minus 5 M) and ammonium ion (K subscript a equals 5.62 x 10 superscript minus 10 M). Horizontal with acetic acid, C H 3 bonded to C that is double bonded to O and bonded to O H is shown interconverting with the same molecule with O H converted to O minus and a free H plus above 4.76 on the p H scale (p K subscript a equals 4.76). Horizontal to ammonium ion, N H 4 superscript plus is shown interchanging with N H 3 plus H plus above 9.25 on the p H scale (p K subscript a equals 9.25). Diprotic acids include carbonic acid and bicarbonate paired and glycine, carboxyl and glycine, amino paired: carbonic acid (K subscript a equals 1.70 x 10 superscript minus 4 M), bicarbonate (K subscript a equals 6.31 x 11 superscript minus 5 M), glycine, carboxyl (K subscript a equals 4.57 x 10 superscript minus 3 M), and glycine, amino (K subscript a equals 2.51 x 10 superscript minus 10 M). Carbonic acid and bicarbonate are shown horizontally across from each other. H 2 C O 3 interconverting with H C O 3 minus plus H plus is above 3.77 on the p H scale (p K subscript a equals 3.77 asterisk) and H C O 3 minus is shown interconverting with C O 3 superscript 2 minus plus H plus above 10.2 on the scale (p K subscript a equals 10.2). Glycine, carboxyl and glycine, amino are shown lined up horizontally. C bonded to 2 H, N H 3 plus, and C that is double bonded to O and bonded to O H interconverts with the same molecule with O H converted to O minus and a free H plus above 2.34 on the pH scale (p K subscript a equals 2.34). C bonded to 2 H, N H 3 plus, and C double bonded to O and bonded to O minus is shown interconverting with the same molecule with N H 2 instead of N H 3 plus and a free H plus above 9.60 on the scale (p K subscript a equals 9.60). Triprotic acids are shown at the bottom of the graph, including phosphoric acid, dihydrogen phosphate, and monohydrogen phosphate grouped together: phosphoric acid (K subscript a equals 7.25 x 10 superscript minus 3 M), dihydrogen phosphate (K subscript a equals 1.38 x 10 superscript minus 7 M), and monohydrogen phosphate (K subscript a equals 1.74 x 10 superscript minus 5 M). Across the bottom of the graph, three reactions are shown. Above 2.14 on the p H scale: H 3 P O 4 interconverts with H 2 P O 4 superscript minus plus H plus, p K subscript a = 2.14. Above 6.86 on the scale: H 2 P O 4 superscript minus interconverts with H P O 4 superscript 2 minus plus H plus; p K subscript a equals 6.86 (with an asterisk symbol). Above 12.4 on the scale: H P O 4 superscript 2 minus interconverts with P O 4 superscript 3 minus plus H plus; p K subscript a equals 12.4.

Each acid has a characteristic tendency to lose its proton in an aqueous solution. The stronger the acid, the greater its tendency to lose its proton. The tendency of any acid (HA) to lose a proton and form its conjugate base $mathml alt text409$ $left-parenthesis upper A Superscript minus Baseline right-parenthesis$ is defined by the equilibrium constant $mathml alt text410$ $left-parenthesis upper K Subscript eq Baseline right-parenthesis$ for the reversible reaction

HA ⇌ H^{+} + A^{-}

$HA right harpoon over left harpoon upper H Superscript plus Baseline plus upper A Superscript minus$

for which

K_{eq} = \frac{[H^{+}] [A^{-}]}{[HA]} = K_{a}

$upper K Subscript eq Baseline equals StartFraction left-bracket upper H Superscript plus Baseline right-bracket left-bracket upper A Superscript minus Baseline right-bracket Over left-bracket HA right-bracket EndFraction equals upper K Subscript a$

Equilibrium constants for ionization reactions are usually called ionization constants or acid dissociation constants, often designated $mathml alt text413$ $upper K Subscript a$ . The dissociation constants of some acids are given in Figure 2-15. Stronger acids, such as phosphoric and carbonic acids, have larger ionization constants; weaker acids, such as monohydrogen phosphate $mathml alt text414$ $left-parenthesis HPO Subscript 4 Superscript 2 minus Baseline right-parenthesis$ , have smaller ionization constants.

Also included in Figure 2-15 are values of ${p K}_{a}$ $bold p bold-italic upper K Subscript bold a$ , which is analogous to pH and is defined by the equation

p K_{a} = \log \frac{1}{K_{a}} = - \log K_{a}

$p upper K Subscript a Baseline equals log StartFraction 1 Over upper K Subscript a Baseline EndFraction equals minus log upper K Subscript a Baseline$

The stronger the tendency to dissociate a proton, the stronger the acid and the lower its $mathml alt text418$ $p upper K Subscript a Baseline$ . As we shall now see, the $mathml alt text419$ $p upper K Subscript a Baseline$ of any weak acid can be determined experimentally.

Titration Curves Reveal the $mathml alt text420$ $bold p bold-italic upper K Subscript bold a Baseline$ of Weak Acids

Titration can be used to determine the amount of an acid in a given solution. A measured volume of the acid is titrated with a solution of a strong base, usually sodium hydroxide (NaOH), of known concentration. The NaOH is added in small increments until the acid is consumed (neutralized), as determined with an indicator dye or a pH meter. The concentration of the acid in the original solution can be calculated from the volume and concentration of NaOH added. The amounts of acid and base in titrations are often expressed in terms of equivalents, where one equivalent is the amount of a substance that will react with, or supply, one mole of hydrogen ions in an acid-base reaction. Recall that for monoprotic acids such as HCl, 1 mol = 1 equivalent; for diprotic acids such as $mathml alt text427$ $upper H Subscript 2 Baseline SO Subscript 4$ , 1 mol = 2 equivalents.

A plot of pH against the amount of NaOH added (a titration curve) reveals the $mathml alt text431$ $p upper K Subscript a Baseline$ of the weak acid. Consider the titration of a 0.1 m solution of acetic acid with 0.1 m NaOH at $mathml alt text434$ $25 degree upper C$ (Fig. 2-16). Two reversible equilibria are involved in the process (here, for simplicity, acetic acid is denoted HAc):

H_{2} O ⇌ H^{+} + {OH}^{-}

$upper H Subscript 2 Baseline upper O right harpoon over left harpoon upper H Superscript plus Baseline plus OH Superscript minus$

(2-5)

HAc ⇌ H^{+} + {Ac}^{-}

$HAc right harpoon over left harpoon upper H Superscript plus Baseline plus Ac Superscript minus$

(2-6)

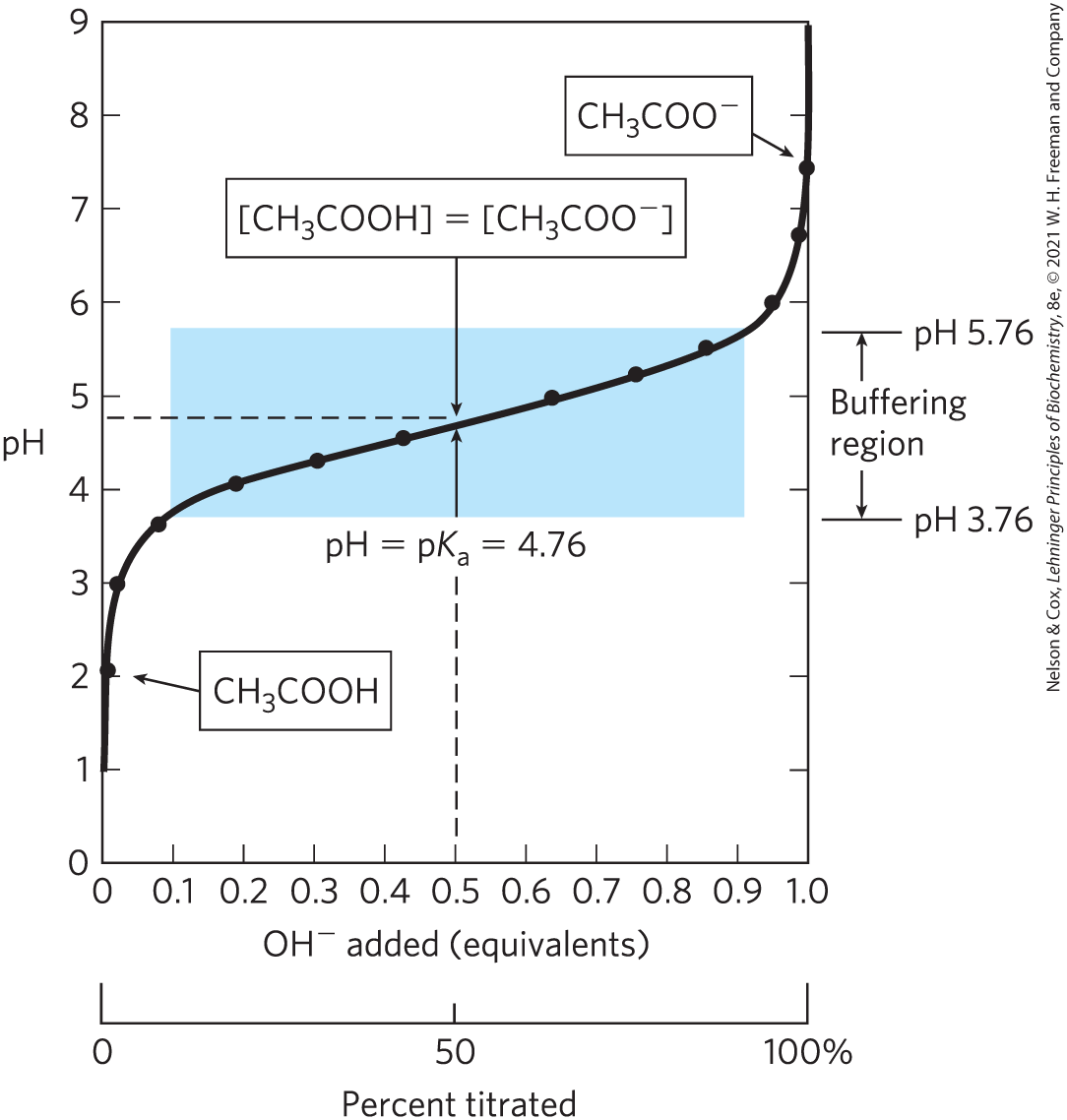
A graph plotting p H against O H minus added shows the titration curve of acetic acid with its buffer region highlighted and with the predominant forms at each p H shown. — FIGURE 2-16 The titration curve of acetic acid. After addition of each increment of NaOH to the acetic acid solution, the pH of the mixture is measured. This value is plotted against the amount of NaOH added, expressed as a fraction of the total NaOH required to convert all the acetic acid $mathml alt text441$ $left-parenthesis CH Subscript 3 Baseline COOH right-parenthesis$ to its deprotonated form, acetate ( $mathml alt text442$ $CH Subscript 3 Baseline COO Superscript minus$ ). The points so obtained yield the titration curve. Shown in the boxes are the predominant ionic forms at the points designated. At the midpoint of the titration, the concentrations of the proton donor and the proton acceptor are equal, and the pH is numerically equal to the $mathml alt text444$ $p upper K Subscript a Baseline$ . The shaded zone is the useful region of buffering power, generally between 10% and 90% titration of the weak acid.

FIGURE 2-16 The titration curve of acetic acid. After addition of each increment of NaOH to the acetic acid solution, the pH of the mixture is measured. This value is plotted against the amount of NaOH added, expressed as a fraction of the total NaOH required to convert all the acetic acid $mathml alt text441$ $left-parenthesis CH Subscript 3 Baseline COOH right-parenthesis$ to its deprotonated form, acetate ( $mathml alt text442$ $CH Subscript 3 Baseline COO Superscript minus$ ). The points so obtained yield the titration curve. Shown in the boxes are the predominant ionic forms at the points designated. At the midpoint of the titration, the concentrations of the proton donor and the proton acceptor are equal, and the pH is numerically equal to the $mathml alt text444$ $p upper K Subscript a Baseline$ . The shaded zone is the useful region of buffering power, generally between 10% and 90% titration of the weak acid.

The graph plots O H minus added (equivalents) on the vertical axis ranging from 0 to 1.0, labeled in increments of 0.1, and p H on the vertical axis ranging from 0 to 9, labeled in increments of 1. The horizontal axis also shows percent titrated ranging from 0 to 100 percent, labeled in increments of 50. The curve rises rapidly, flattens around a p H of 4.76, then begins to rise more rapidly at about a p H of 0.9. The curve begins at (0, 1) and passes through the points (0.01, 2), (0.015, 3), (0.1, 3.9), (0.2, 4), (0.3, 4.5), (0.4, 4.75), (0.5, 4.76), (0.69, 5.25), (0.78, 5.5), (0.88, 5.9), (0.96, 6.5), and (1.0, 7) before ending at (1.0, 9). An arrow pointing to the start of the curve reads, C H 3 C O O H. An arrow pointing to the end of the curve reads, C H 3 C O O minus. A dotted line from 0.5 on the horizontal axis to the curve shows the location where the concentration of C H 3 C O O H equals the concentration of C H 3 C O O minus. Below the relatively flat line at this point, an equation reads, p H equals p K subscript a equals 4.76. The buffering region is labeled as the zone between p H 3.76 and p H 5.76. All data are approximate.

The equilibria must simultaneously conform to their characteristic equilibrium constants, which are, respectively,

K_{w} = [H^{+}] [{OH}^{-}] = 1 \times 10^{- 14} M^{2}

$upper K Subscript w Baseline equals left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket equals 1 times 10 Superscript negative 14 Baseline upper M Superscript 2$

(2-7)

K_{a} = \frac{[H^{+}] [{Ac}^{-}]}{[HAc]} = 1.74 \times 10^{- 5} M

$upper K Subscript a Baseline equals StartFraction left-bracket upper H Superscript plus Baseline right-bracket left-bracket Ac Superscript minus Baseline right-bracket Over left-bracket HAc right-bracket EndFraction equals 1.74 times 10 Superscript negative 5 Baseline upper M$

(2-8)

At the beginning of the titration, before any NaOH is added, the acetic acid is already slightly ionized, to an extent that can be calculated from its ionization constant (Eqn 2-8).

As NaOH is gradually introduced, the added $mathml alt text451$ $OH Superscript minus$ combines with the free $mathml alt text452$ $upper H Superscript plus$ in the solution to form $mathml alt text453$ $upper H Subscript 2 Baseline upper O$ , to an extent that satisfies the equilibrium relationship in Equation 2-7. As free $mathml alt text454$ $upper H Superscript plus$ is removed, HAc dissociates further to satisfy its own equilibrium constant (Eqn 2-8). The net result as the titration proceeds is that more and more HAc ionizes, forming $mathml alt text455$ $Ac Superscript minus$ , as the NaOH is added. At the midpoint of the titration, at which exactly 0.5 equivalent of NaOH has been added per equivalent of the acid, one-half of the original acetic acid has undergone dissociation, so that the concentration of the proton donor, [HAc], now equals that of the proton acceptor, $mathml alt text458$ $left-bracket Ac Superscript minus Baseline right-bracket$ . At this midpoint a very important relationship holds: the pH of the equimolar solution of acetic acid and acetate is exactly equal to the $mathml alt text460$ $p upper K Subscript a Baseline$ of acetic acid ( $mathml alt text461$ $p upper K Subscript a Baseline equals 4.76$ ; Figs 2-15, 2-16). The basis for this relationship, which holds for all weak acids, will soon become clear.

As the titration is continued by adding further increments of NaOH, the remaining nondissociated acetic acid is gradually converted into acetate. The end point of the titration occurs at about pH 7.0: all the acetic acid has lost its protons to $mathml alt text464$ $OH Superscript minus$ , to form $mathml alt text465$ $upper H Subscript 2 Baseline upper O$ and acetate. Throughout the titration the two equilibria (Eqns 2-5, 2-6) coexist, each always conforming to its equilibrium constant.

Figure 2-17 compares the titration curves of three weak acids with very different ionization constants: acetic acid ( $mathml alt text466$ $p upper K Subscript a Baseline equals 4.76$ ); dihydrogen phosphate, $upper H Subscript 2 Baseline PO Subscript 4 Superscript minus$ $upper H Subscript 2 Baseline PO Subscript 4 Superscript minus$ $mathml alt text468$ $left-parenthesis p upper K Subscript a Baseline equals 6.86 right-parenthesis$ ; and ammonium ion, $mathml alt text469$ $NH Subscript 4 Superscript plus$ ( $mathml alt text470$ $p upper K Subscript a Baseline equals 9.25$ ). Although the titration curves of these acids have the same shape, they are displaced along the pH axis because the three acids have different strengths. Acetic acid, with the highest $mathml alt text472$ $upper K Subscript a$ (lowest $mathml alt text473$ $p upper K Subscript a Baseline$ ) of the three, is the strongest of the three weak acids (loses its proton most readily); it is already half dissociated at pH 4.76. Dihydrogen phosphate loses a proton less readily, being half dissociated at pH 6.86. Ammonium ion is the weakest acid of the three and does not become half dissociated until pH 9.25. The titration curve of these weak acids shows graphically that a weak acid and its anion—a conjugate acid-base pair—can act as a buffer, as we describe in the next section.

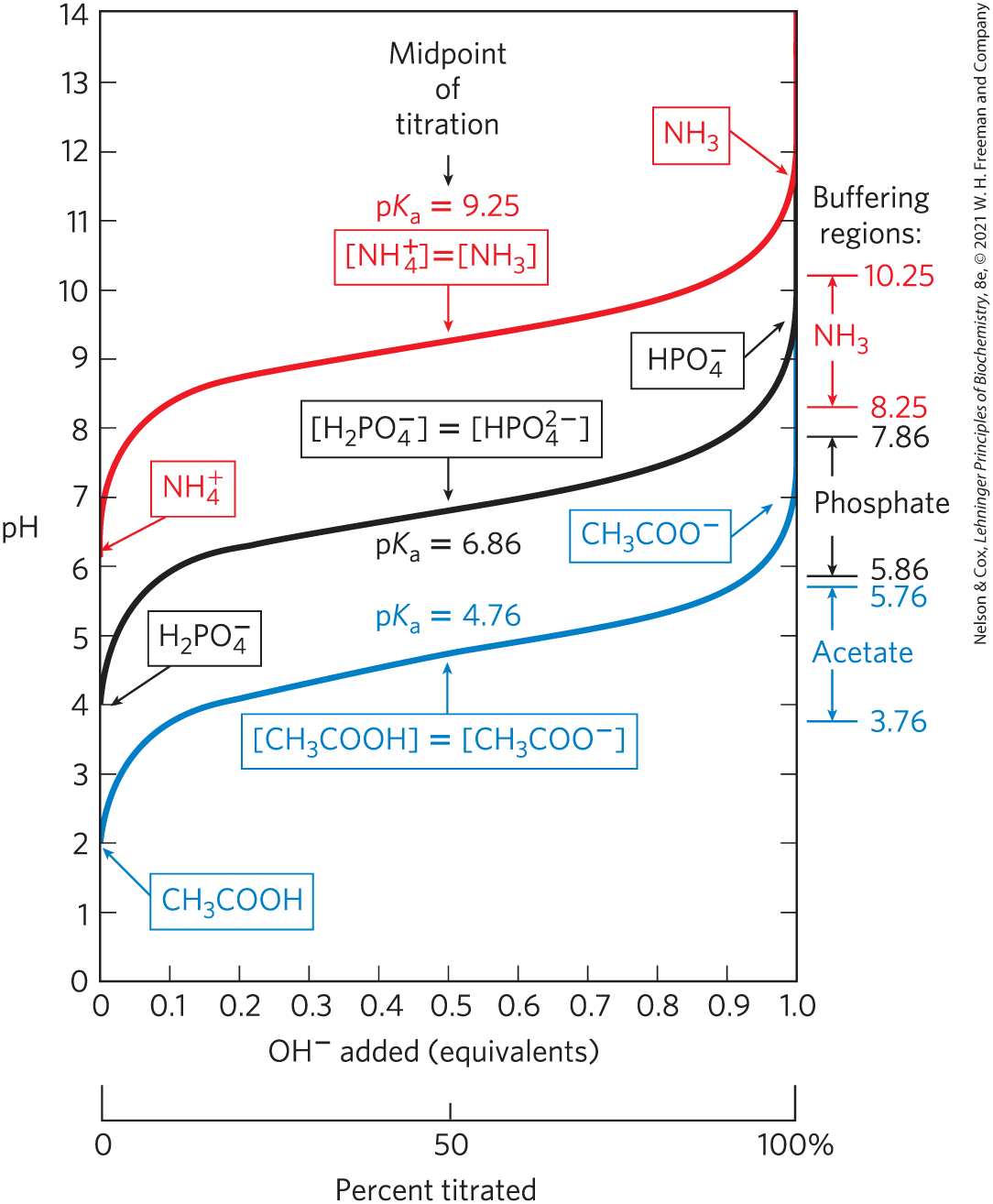
A graph compares titration curves for C H 3 C O O H, H 2 P O 4 minus, and N H 4 plus, showing the predominant forms at different p Hs and buffering regions for each. — FIGURE 2-17 Comparison of the titration curves of three weak acids. Shown here are the titration curves for $mathml alt text477$ $CH Subscript 3 Baseline COOH$ , $mathml alt text478$ $upper H Subscript 2 Baseline PO Subscript 4 Superscript minus$ , and $mathml alt text479$ $NH Subscript 4 Superscript plus$ . The predominant ionic forms at designated points in the titration are given in boxes. The regions of buffering capacity are indicated at the right. Conjugate acid-base pairs are effective buffers between approximately 10% and 90% neutralization of the proton-donor species.

FIGURE 2-17 Comparison of the titration curves of three weak acids. Shown here are the titration curves for $mathml alt text477$ $CH Subscript 3 Baseline COOH$ , $mathml alt text478$ $upper H Subscript 2 Baseline PO Subscript 4 Superscript minus$ , and $mathml alt text479$ $NH Subscript 4 Superscript plus$ . The predominant ionic forms at designated points in the titration are given in boxes. The regions of buffering capacity are indicated at the right. Conjugate acid-base pairs are effective buffers between approximately 10% and 90% neutralization of the proton-donor species.

The graph plots O H minus added (equivalents) on the vertical axis, ranging from 0 to 1.0, labeled in increments of 0.1, and p H on the vertical axis, ranging from 0 to 14, labeled in increments of 1. The horizontal axis also shows percent titrated, ranging from 0 to 100 percent, labeled in increments of 50. All curves have a similar shape. The top curve begins at about (0, 6.2), N H 4 superscript plus, curves up rapidly to about (0.15, 8.25), levels off across the middle of the graph, then curves upward more rapidly from (0.95, 10.25) until the curve runs along the right side of the graph beginning at (10, 11.5), N H 3. At the midpoint of titration at (0.5, 9.25), concentration of N H 4 plus equals concentration of N H 3 (p K subscript a equals 9.25). The buffering region is 8.25 to 10.25. The middle curve begins at about (0, 4), H 2 P O 4 superscript minus, curves up rapidly to about (0.15, 5.86), levels off across the middle of the graph, then curves upward more rapidly from (0.95, 7.86) until the curve runs along the right side of the graph beginning at (10, 9.3), H P O 4 superscript minus. At the midpoint of titration at (0.5, 6.86), concentration of H P O 4 superscript minus equals concentration of H P O 4 superscript minus 2 (p K subscript a equals 6.86). The buffering region is 5.86 to 7.86. The bottom curve begins at about (0, 2), C H 3 C O O O H, curves up rapidly to about (0.15, 3.76), levels off across the middle of the graph, then curves upward more rapidly from (0.95, 5.76) until the curve runs along the right side of the graph beginning at (10, 7), C H 3 C O O superscript minus. At the midpoint of titration at (0.5, 4.76), concentration of C H 3 C O O H equals concentration of C H 3 C O O superscript minus (p K subscript a equals 4.76). The buffering region is 3.76 to 5.76. All data are approximate.

Like all equilibrium constants, $mathml alt text482$ $upper K Subscript a$ and $mathml alt text483$ $p upper K Subscript a Baseline$ are defined for specific conditions of concentration (components at 1 m) and temperature $mathml alt text485$ $left-parenthesis 25 degree upper C right-parenthesis$ . Concentrated buffer solutions do not show ideal behavior. For example, the $mathml alt text486$ $p upper K Subscript a Baseline$ of dihydrogen phosphate is sometimes given as 7.2, sometimes as 6.86. The higher value (the apparent $mathml alt text489$ $p upper K Subscript a Baseline$ ) is not corrected for the effects of buffer concentration, and is defined at a temperature of $mathml alt text490$ $25 degree upper C$ . The value of 6.86 is corrected for buffer concentration and measured at physiological temperature $mathml alt text492$ $left-parenthesis 37 degree upper C right-parenthesis$ , and is probably a closer approximation to the relevant value of $mathml alt text493$ $p upper K Subscript a Baseline$ in warm-blooded animals. We therefore use the value $mathml alt text494$ $p upper K Subscript a Baseline equals 6.86$ for dihydrogen phosphate throughout this book.

SUMMARY 2.2 Ionization of Water, Weak Acids, and Weak Bases

Pure water ionizes slightly, forming equal numbers of hydrogen ions (hydronium ions, $mathml alt text495$ $upper H Subscript 3 Baseline upper O Superscript plus$ ) and hydroxide ions.
The extent of ionization is described by an equilibrium constant, $mathml alt text496$ $upper K Subscript eq Baseline equals StartFraction left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket Over left-bracket upper H Subscript 2 Baseline upper O right-bracket EndFraction comma$ from which the ion product of water, $mathml alt text497$ $upper K Subscript w$ , is derived. At $mathml alt text498$ $25 degree upper C$ , $mathml alt text499$ $upper K Subscript w Baseline equals left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket equals left-parenthesis 55.5 upper M right-parenthesis left-parenthesis upper K Subscript eq Baseline right-parenthesis equals 10 Superscript Number minus 1 4 Baseline upper M squared$
The pH of an aqueous solution reflects, on a logarithmic scale, the concentration of hydrogen ions:
$pH = \log \frac{1}{[H^{+}]} = - \log [H^{+}]$ $pH equals log StartFraction 1 Over left-bracket upper H Superscript plus Baseline right-bracket EndFraction equals minus log left-bracket upper H Superscript plus Baseline right-bracket$
Weak acids partially ionize to release a hydrogen ion, thus lowering the pH of the aqueous solution. Weak bases accept a hydrogen ion, increasing the pH. The extent of these processes is characteristic of each particular weak acid or base and is expressed as an acid dissociation constant:

$K_{eq} = \frac{[H^{+}] [A^{-}]}{[HA]} = K_{a}$ $upper K Subscript eq Baseline equals StartFraction left-bracket upper H Superscript plus Baseline right-bracket left-bracket upper A Superscript minus Baseline right-bracket Over left-bracket HA right-bracket EndFraction equals upper K Subscript a$
The $mathml alt text505$ $p upper K Subscript a Baseline$ expresses, on a logarithmic scale, the relative strength of a weak acid or base:

$p K_{a} = \log \frac{1}{[K_{a}]} = - \log K_{a}$ $p upper K Subscript a Baseline equals log StartFraction 1 Over left-bracket upper K Subscript a Baseline right-bracket EndFraction equals minus log upper K Subscript a Baseline$
The stronger the acid, the smaller its $mathml alt text507$ $p upper K Subscript a Baseline$ ; the stronger the base, the larger the $mathml alt text508$ $p upper K Subscript a Baseline$ of its conjugate acid. The $mathml alt text509$ $p upper K Subscript a Baseline$ can be determined experimentally; it is the pH at the midpoint of the titration curve.