2.1 Weak Interactions in Aqueous Systems
Hydrogen bonds between water molecules provide the cohesive forces that make water a liquid at room temperature and a crystalline solid (ice) with a highly ordered arrangement of molecules at cold temperatures. Polar biomolecules dissolve readily in water because they can replace water-water interactions with energetically favorable water-solute interactions. In contrast, nonpolar biomolecules are poorly soluble in water because they interfere with water-water interactions but are unable to form water-solute interactions. In aqueous solutions, nonpolar molecules tend to cluster together. Hydrogen bonds and ionic, hydrophobic (from the Greek, meaning “water-fearing”), and van der Waals interactions are individually weak, but collectively they have a very significant influence on the three-dimensional structures of proteins, nucleic acids, polysaccharides, and membrane lipids.
Hydrogen Bonding Gives Water Its Unusual Properties
Water has a higher melting point, boiling point, and heat of vaporization than most other common solvents. These unusual properties are a consequence of attractions between adjacent water molecules that give liquid water great internal cohesion. A look at the electron structure of the molecule reveals the cause of these intermolecular attractions.
Each hydrogen atom of a water molecule shares an electron pair with the central oxygen atom. The geometry of the molecule is dictated by the shapes of the outer electron orbitals of the oxygen atom, which are similar to the bonding orbitals of carbon (see Fig. 1-13). These orbitals describe a rough tetrahedron, with a hydrogen atom at each of two corners and nonbonding orbitals at the other two corners (Fig. 2-1a). The bond angle is , slightly less than the of a perfect tetrahedron because of crowding by the nonbonding orbitals of the oxygen atom.
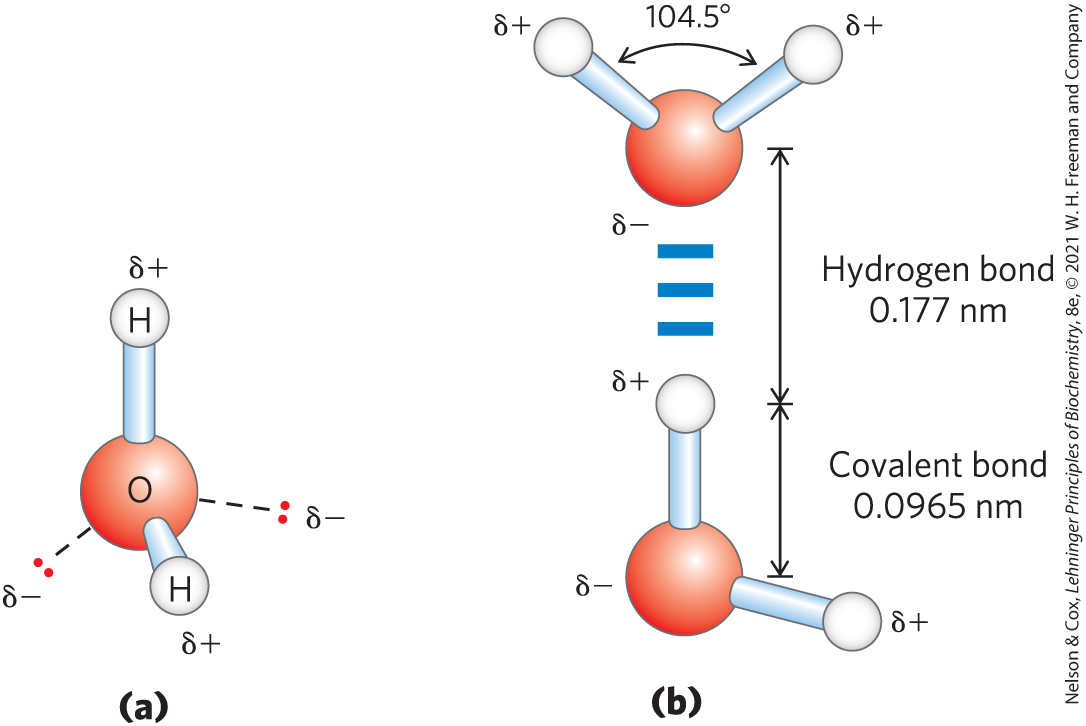
FIGURE 2-1 Structure of the water molecule. (a) The dipolar nature of the molecule is shown in a ball-and-stick model; the dashed lines represent the nonbonding orbitals. There is a nearly tetrahedral arrangement of the outer-shell electron pairs around the oxygen atom; the two hydrogen atoms have localized partial positive charges (δ+), and the oxygen atom has a partial negative charge (δ−). (b) Two molecules are joined by a hydrogen bond (designated here, and throughout this book, by three blue lines) between the oxygen atom of the upper molecule and a hydrogen atom of the lower one. Hydrogen bonds are longer and weaker than covalent bonds.
The oxygen nucleus attracts electrons more strongly than does the hydrogen nucleus (a proton); that is, oxygen is more electronegative. This means that the shared electrons are more often in the vicinity of the oxygen atom than of the hydrogen. The result of this unequal electron sharing is two electric dipoles in the water molecule, one along each of the bonds; each hydrogen atom bears a partial positive charge (δ+), and the oxygen atom bears a partial negative charge equal in magnitude to the sum of the two partial positives . As a result, there is an electrostatic attraction between the oxygen atom of one water molecule and the hydrogen of another (Fig. 2-1b), called a hydrogen bond. Throughout this book, we represent hydrogen bonds with three parallel blue lines, as in Figure 2-1b.
Hydrogen bonds are relatively weak. Those in liquid water have a bond dissociation energy (the energy required to break a bond) of about 23 kJ/mol, compared with 470 kJ/mol for the covalent bond in water or 350 kJ/mol for a covalent bond. The hydrogen bond is about 10% covalent, due to overlaps in the bonding orbitals, and about 90% electrostatic. At room temperature, the thermal energy of an aqueous solution (the kinetic energy of motion of the individual atoms and molecules) is of the same order of magnitude as that required to break hydrogen bonds. When water is heated, the increase in temperature reflects the faster motion of individual water molecules. At any given time, most of the molecules in liquid water are hydrogen-bonded, but the lifetime of each hydrogen bond is just 1 to 20 picoseconds ; when one hydrogen bond breaks, another hydrogen bond forms, with the same partner or a new one, within 0.1 ps. The apt phrase “flickering clusters” has been applied to the short-lived groups of water molecules interlinked by hydrogen bonds in liquid water. The sum of all the hydrogen bonds between molecules confers great internal cohesion on liquid water. Extended networks of hydrogen-bonded water molecules also form bridges between solutes (proteins and nucleic acids, for example) that allow the larger molecules to interact with each other over distances of several nanometers without physically touching.
The nearly tetrahedral arrangement of the orbitals about the oxygen atom (Fig. 2-1a) allows each water molecule to form hydrogen bonds with as many as four neighboring water molecules. In liquid water at room temperature and atmospheric pressure, however, water molecules are disorganized and in continuous motion, so that each molecule forms hydrogen bonds with an average of only 3.4 other molecules. In ice, on the other hand, each water molecule is fixed in space and forms hydrogen bonds with a full complement of four other water molecules to yield a regular lattice structure (Fig. 2-2). Hydrogen bonds account for the relatively high melting point of water, because much thermal energy is required to break a sufficient proportion of hydrogen bonds to destabilize the crystal lattice of ice. When ice melts or water evaporates, heat is taken up by the system:
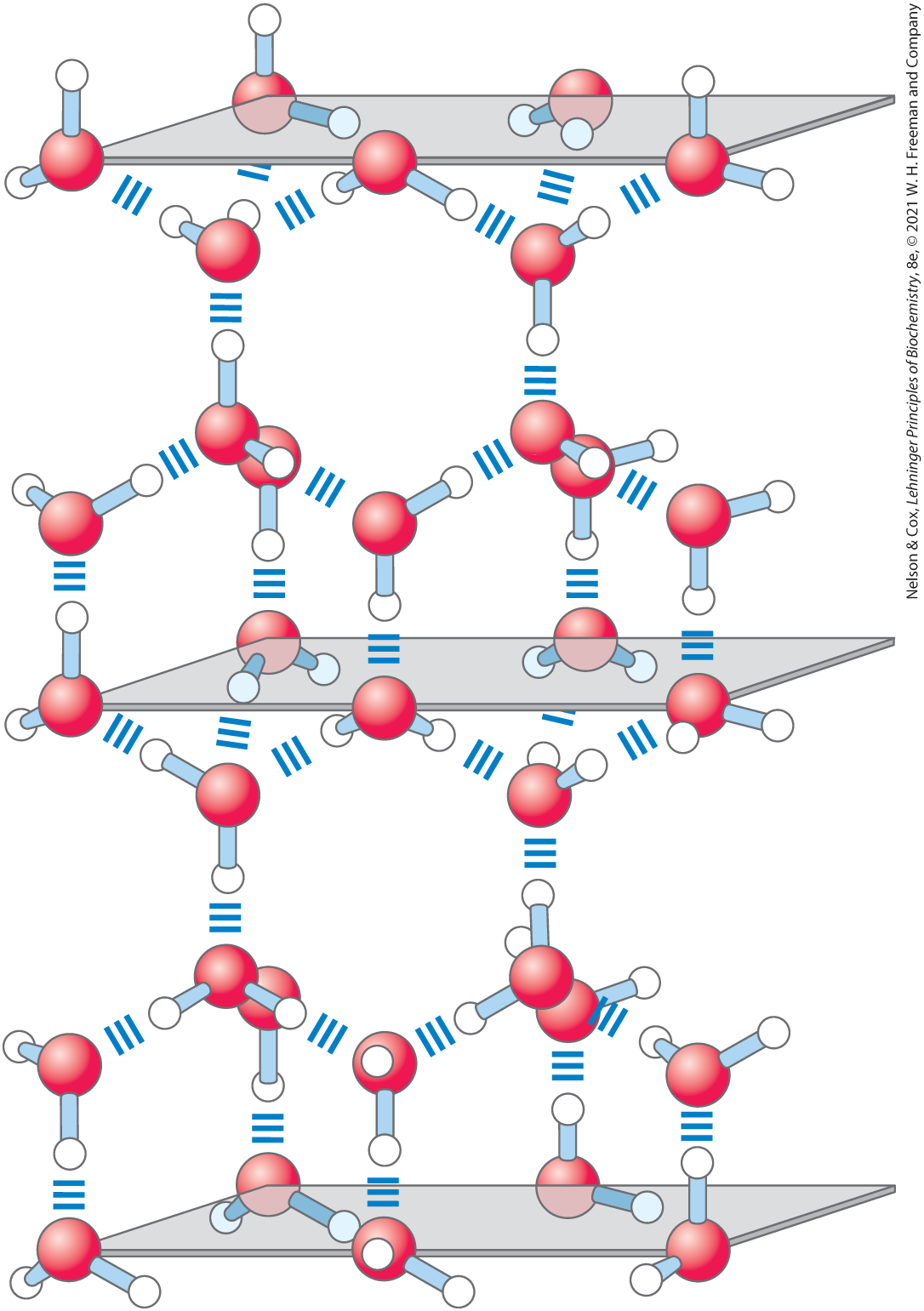
FIGURE 2-2 Hydrogen bonding in ice. In ice, each water molecule forms four hydrogen bonds, the maximum possible for a water molecule, creating a regular crystal lattice. By contrast, in liquid water at room temperature and atmospheric pressure, each water molecule hydrogen-bonds with an average of 3.4 other water molecules. This crystal lattice structure makes ice less dense than liquid water, and thus ice floats on liquid water.
During melting or evaporation, the entropy of the aqueous system increases as the highly ordered arrays of water molecules in ice relax into the less orderly hydrogen-bonded arrays in liquid water or into the wholly disordered gaseous state. At room temperature, both the melting of ice and the evaporation of water occur spontaneously; the tendency of the water molecules to associate through hydrogen bonds is outweighed by the energetic push toward randomness. Recall that the free-energy change (ΔG) must have a negative value for a process to occur spontaneously: ΔG = ΔH − TΔS, where ΔG represents the driving force, ΔH the enthalpy change from making and breaking bonds, and ΔS the change in randomness. Because ΔH is positive for melting and evaporation, it is clearly the increase in entropy (ΔS) that makes ΔG negative and drives these changes.
Water Forms Hydrogen Bonds with Polar Solutes
Hydrogen bonds are not unique to water. They readily form between an electronegative atom (the hydrogen acceptor, usually oxygen or nitrogen) and a hydrogen atom covalently bonded to another electronegative atom (the hydrogen donor) in the same or another molecule (Fig. 2-3). Hydrogen atoms covalently bonded to carbon atoms do not participate in hydrogen bonding, because carbon is only slightly more electronegative than hydrogen and thus the bond is only very weakly polar. The distinction explains why butane has a boiling point of only , whereas butanol has a relatively high boiling point of . Butanol has a polar hydroxyl group and thus can form intermolecular hydrogen bonds. Uncharged but polar biomolecules such as sugars dissolve readily in water because of the stabilizing effect of hydrogen bonds between the hydroxyl groups or carbonyl oxygen of the sugar and the polar water molecules. Alcohols, aldehydes, ketones, and compounds containing bonds all form hydrogen bonds with water molecules (Fig. 2-4) and tend to be soluble in water.
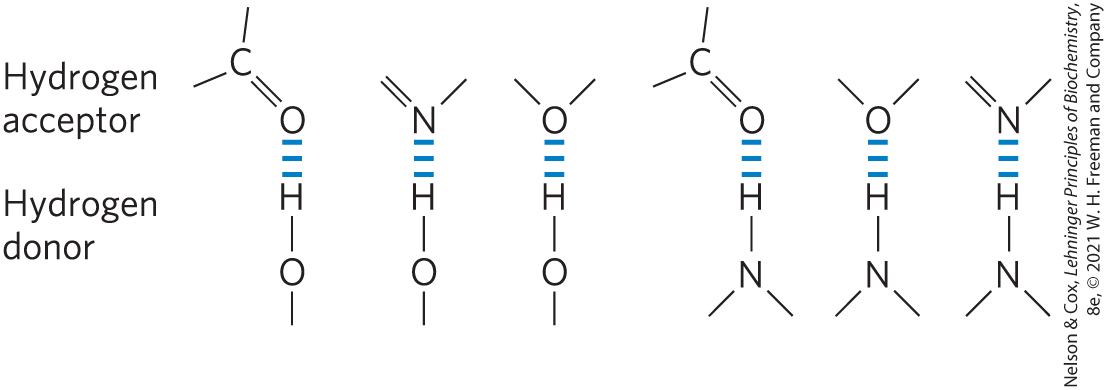
FIGURE 2-3 Common hydrogen bonds in biological systems. The hydrogen acceptor is usually oxygen or nitrogen; the hydrogen donor is another electronegative atom.
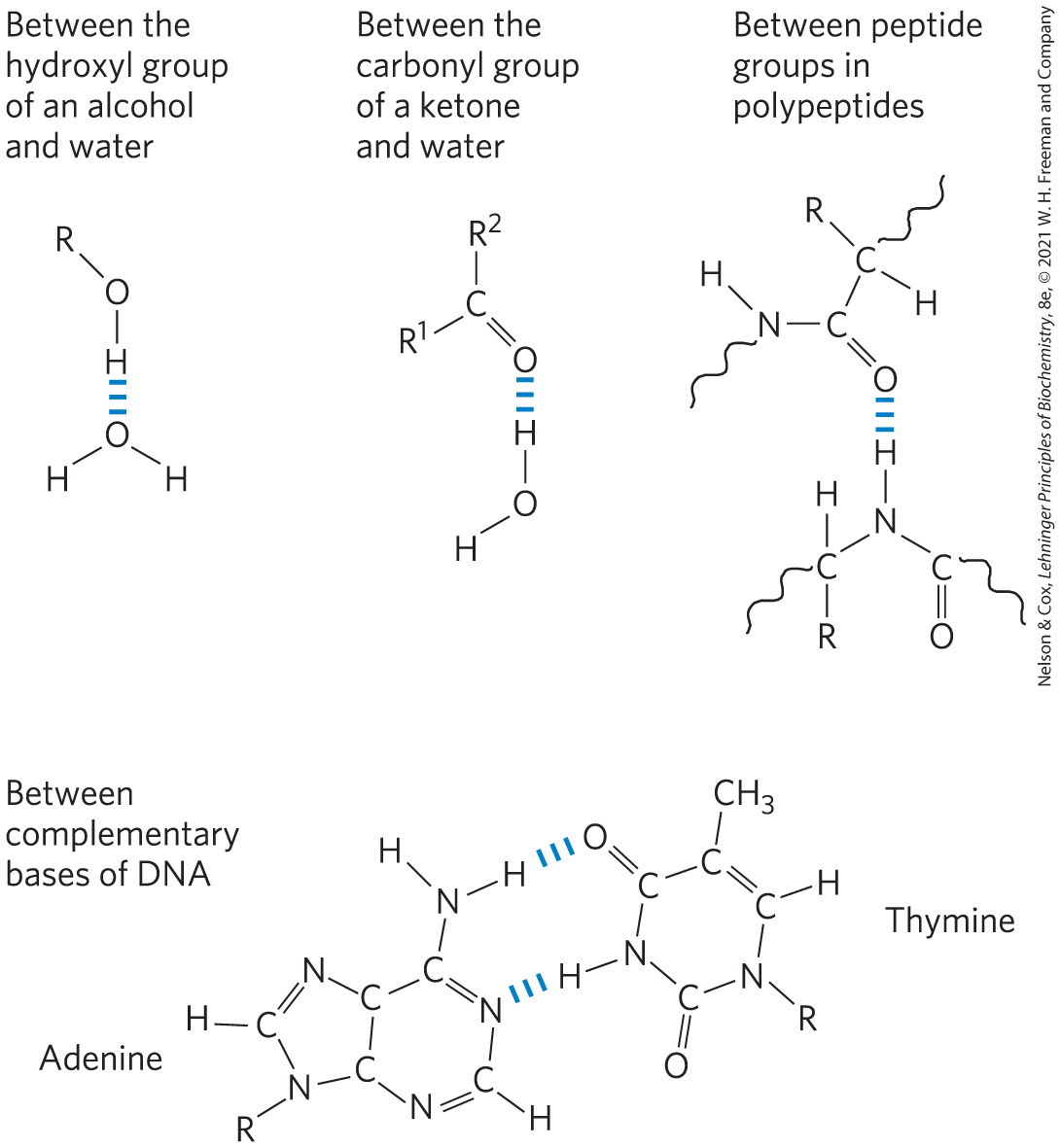
FIGURE 2-4 Some biologically important hydrogen bonds.
Hydrogen bonds are strongest when the bonded molecules are oriented to maximize electrostatic interaction, which occurs when the hydrogen atom and the two atoms that share it are in a straight line—that is, when the acceptor atom is in line with the covalent bond between the donor atom and H (Fig. 2-5). This arrangement puts the positive charge of the hydrogen ion directly between the two partial negative charges. Hydrogen bonds are thus highly directional and capable of holding two hydrogen-bonded molecules or groups in a specific geometric arrangement. As we shall see, this property of hydrogen bonds confers very precise three-dimensional structures on protein and nucleic acid molecules, which have many intramolecular hydrogen bonds.
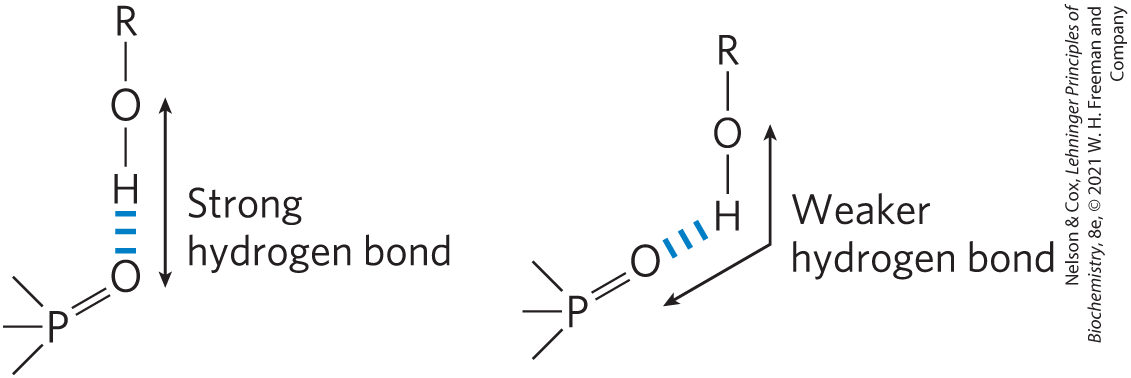
FIGURE 2-5 Directionality of the hydrogen bond. The attraction between the partial electric charges is greatest when the three atoms involved in the bond (in this case O, H, and O) lie in a straight line. When the hydrogen-bonded moieties are structurally constrained (when they are parts of a single protein molecule, for example), this ideal geometry may not be possible and the resulting hydrogen bond is weaker.
Water Interacts Electrostatically with Charged Solutes
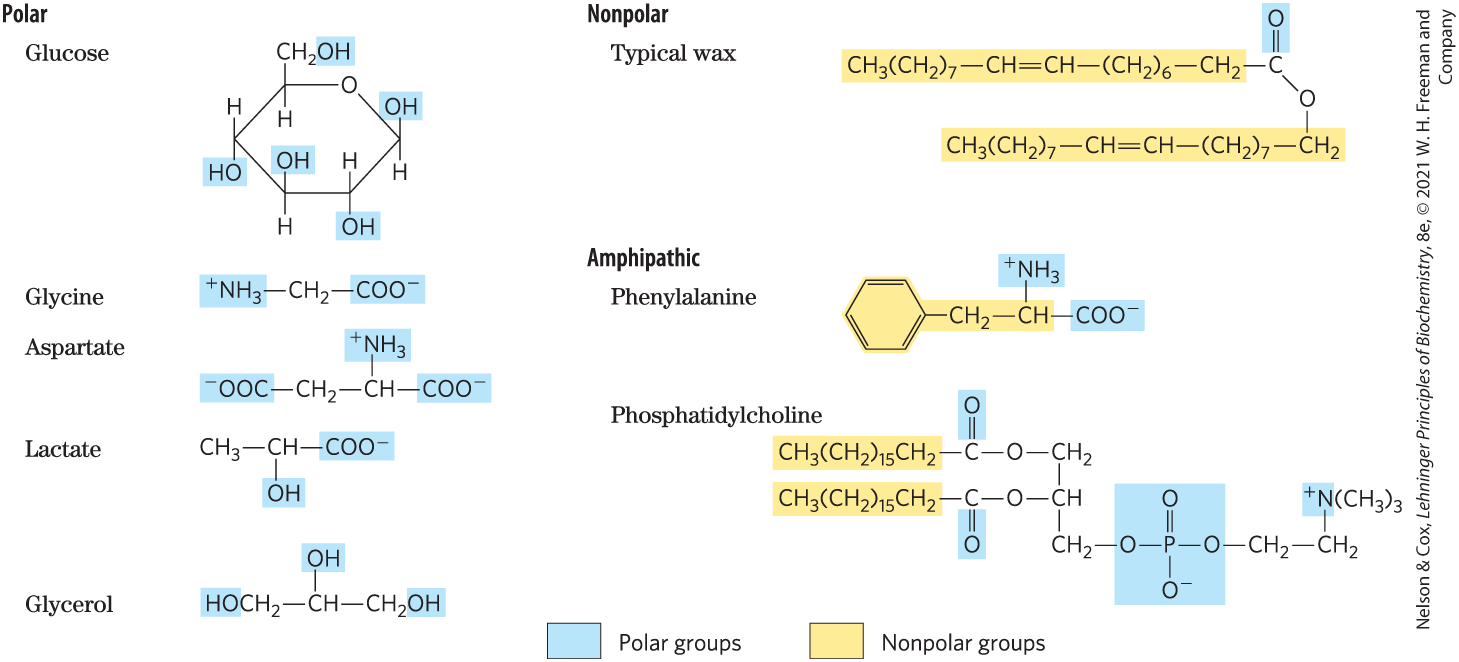
Water is a polar solvent. It readily dissolves most biomolecules, which are generally charged or polar compounds (Table 2-1); compounds that dissolve easily in water are hydrophilic (from the Greek, meaning “water-loving”). In contrast, nonpolar solvents such as chloroform and benzene are poor solvents for polar biomolecules but easily dissolve those that are hydrophobic—nonpolar molecules such as lipids and waxes. Amphipathic compounds contain regions that are polar (or charged) and regions that are nonpolar. Their behavior in aqueous solution is discussed on p. 48.
Water dissolves salts such as NaCl by hydrating and stabilizing the and ions, weakening the electrostatic interactions between them and thus counteracting their tendency to associate in a crystalline lattice (Fig. 2-6). Water also readily dissolves charged biomolecules, including compounds with functional groups such as ionized carboxylic acids , protonated amines , and phosphate esters or anhydrides. Water replaces the solute-solute hydrogen bonds linking these biomolecules to each other with solute-water hydrogen bonds, thus screening the electrostatic interactions between solute molecules.
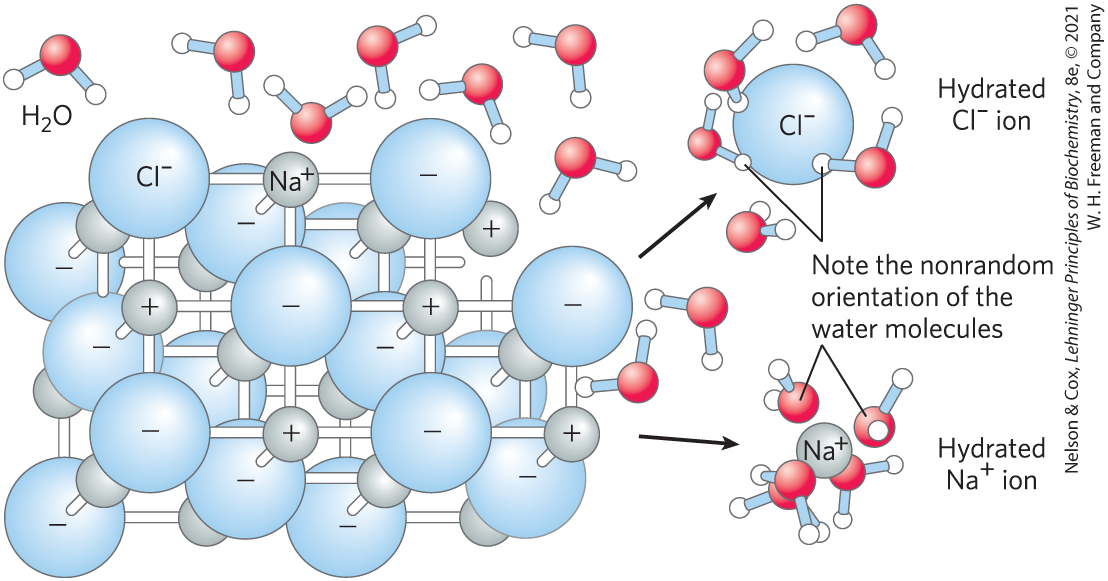
FIGURE 2-6 Water as solvent. Water dissolves many crystalline salts by hydrating their component ions. The NaCl crystal lattice is disrupted as water molecules cluster about the and ions. The ionic charges are partially neutralized, and the electrostatic attractions necessary for lattice formation are weakened.
Ionic interactions between dissolved ions are much stronger in less polar environments, because there is less screening of charges by the nonpolar solvent. Water is effective in screening the electrostatic interactions between dissolved ions because it has a high dielectric constant, a physical property that reflects the number of dipoles in a solvent. The strength, or force (F), of ionic interactions in a solution depends on the magnitude of the charges (Q), the distance between the charged groups (r), and the dielectric constant (ε, which is dimensionless) of the solvent in which the interactions occur:
For water at , ε is 78.5, and for the very nonpolar solvent benzene, ε is 4.6. The dependence on is such that ionic attractions or repulsions operate only over short distances—in the range of 10 to 40 nm (depending on the electrolyte concentration) when the solvent is water. In biomolecules, it is not the dielectric constant for the bulk solvent, but the highly localized dielectric constant, as in a hydrophobic pocket of a protein, that determines the interaction of two polar moieties.
As a salt such as NaCl dissolves, the and ions leaving the crystal lattice acquire far greater freedom of motion (Fig. 2-6). The resulting increase in entropy (randomness) of the system is largely responsible for the ease of dissolving salts such as NaCl in water. In thermodynamic terms, formation of the solution occurs with a favorable free-energy change: ΔG = ΔH − TΔS, where ΔH has a small positive value and TΔS a large positive value; thus ΔG is negative.
Nonpolar Gases Are Poorly Soluble in Water
The biologically important gases , , and are nonpolar molecules. In and , electrons are shared equally by both atoms. In , each bond is polar, but the two dipoles are oppositely directed and cancel each other (Table 2-2). The movement of molecules from the disordered gas phase into aqueous solution constrains their motion and the motion of water mole-cules and therefore represents a decrease in entropy. The nonpolar nature of these gases and the decrease in entropy when they enter solution combine to make them very poorly soluble in water. Some organisms have water-soluble “carrier proteins” (hemoglobin and myoglobin, for example) that facilitate the transport of . Carbon dioxide forms carbonic acid in aqueous solution and is transported as the (bicarbonate) ion, either free—bicarbonate is very soluble in water —or bound to hemoglobin. Three other gases, , NO, and , also have biological roles in some organisms; these gases are polar and dissolve readily in water.
| Gas | Structurea | Polarity | Solubility in water (g/L)b |
|---|---|---|---|
Nitrogen |
Nonpolar |
||
Oxygen |
Nonpolar |
||
Carbon dioxide |
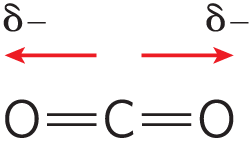
|
Nonpolar |
|
Ammonia |
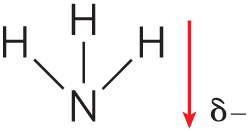
|
Polar |
|
Hydrogen sulfide |
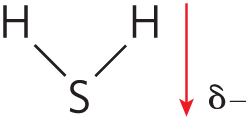
|
Polar |
|
aThe arrows represent electric dipoles; there is a partial negative charge (δ−) at the head of the arrow, a partial positive charge (δ+; not shown here) at the tail. bNote that polar molecules dissolve far better even at low temperatures than do nonpolar molecules at relatively high temperatures. |
|||
Nonpolar Compounds Force Energetically Unfavorable Changes in the Structure of Water
When water is mixed with benzene or hexane, two phases form; neither liquid is soluble in the other. Nonpolar compounds such as benzene and hexane are hydrophobic—they are unable to undergo energetically favorable interactions with water molecules, and they interfere with the hydrogen bonding among water molecules. All molecules or ions in aqueous solution interfere with the hydrogen bonding of some water molecules in their immediate vicinity, but polar or charged solutes (such as NaCl) compensate for lost water-water hydrogen bonds by forming new solute-water interactions. The net change in enthalpy (ΔH) for dissolving these solutes is generally small. Hydrophobic solutes, however, offer no such compensation, and their addition to water may therefore result in a small gain of enthalpy; the breaking of hydrogen bonds between water molecules takes up energy from the system, requiring the input of energy from the surroundings. In addition to requiring this input of energy, dissolving hydrophobic compounds in water produces a measurable decrease in entropy. Water molecules in the immediate vicinity of a nonpolar solute are constrained in their possible orientations, as they form a highly ordered cagelike shell around each solute molecule to maximize solvent-solvent hydrogen bonding. These water molecules are not as highly oriented as those in clathrates, crystalline compounds of nonpolar solutes and water, but the effect is the same in both cases: the ordering of water molecules reduces entropy. The number of ordered water molecules, and therefore the magnitude of the entropy decrease, is proportional to the surface area of the hydrophobic solute enclosed within the cage of water molecules. The free-energy change for dissolving a nonpolar solute in water is thus unfavorable: ΔG = ΔH − TΔS, where ΔH has a positive value, ΔS has a negative value, and ΔG is positive.
When an amphipathic compound (Table 2-1) is mixed with water, the polar, hydrophilic region interacts favorably with the water and tends to dissolve, but the nonpolar, hydrophobic region tends to avoid contact with the water (Fig. 2-7a). The nonpolar regions of the molecules cluster together to present the smallest hydrophobic area to the aqueous solvent, and the polar regions are arranged to maximize their interaction with each other and with the solvent (Fig. 2-7b), a phenomenon called the hydrophobic effect. These stable structures of amphipathic compounds in water, called micelles, may contain hundreds or thousands of molecules. By clustering together, nonpolar regions of the molecules achieve the greatest thermodynamic stability by minimizing the number of ordered water molecules required to surround hydrophobic portions of the solute molecules, increasing the entropy of the system. A special case of this hydrophobic effect is the formation of lipid bilayers in biological membranes (see Fig. 11-1).
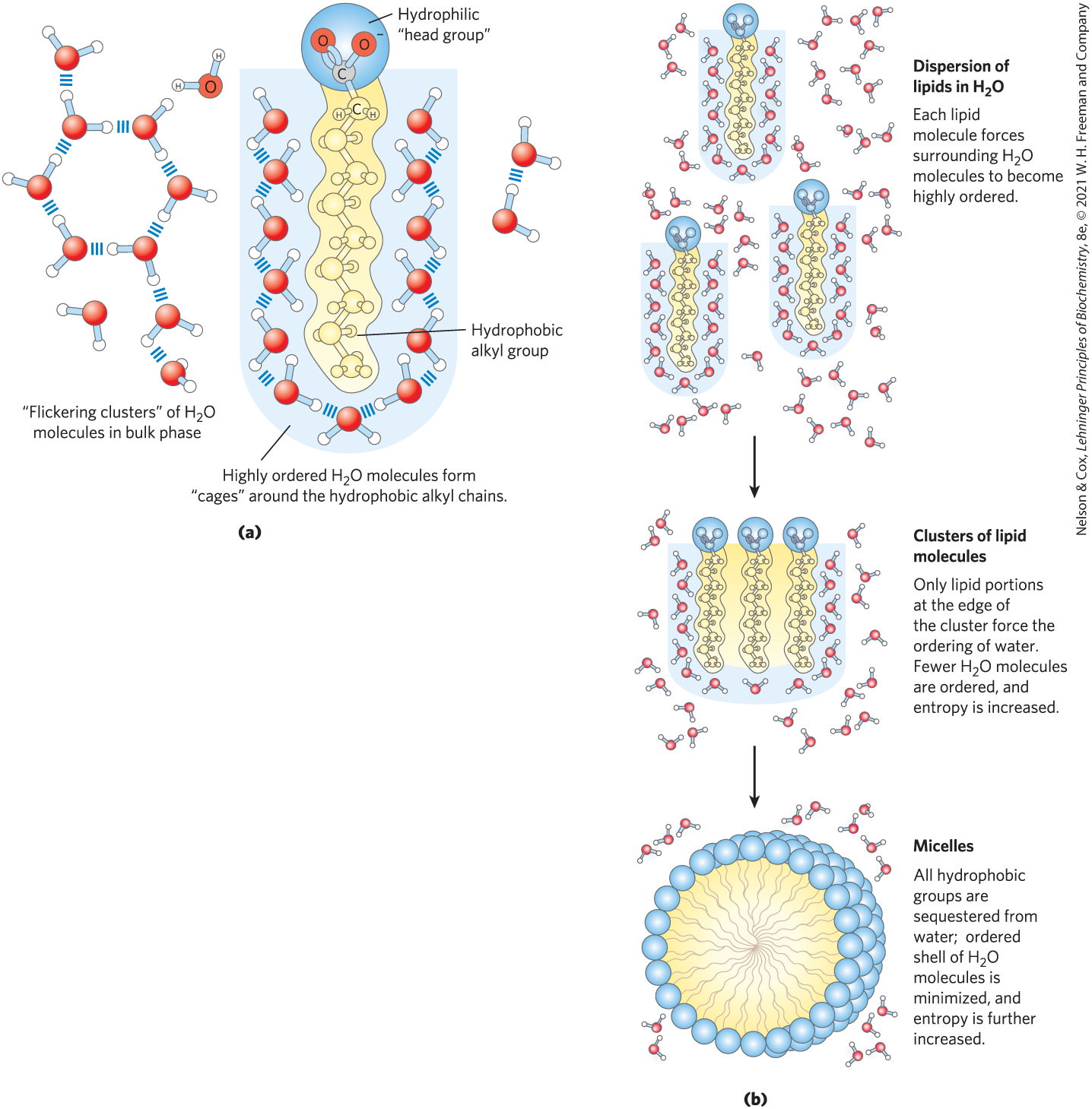
FIGURE 2-7 Amphipathic compounds in aqueous solution form structures that increase entropy. (a) Long-chain fatty acids have very hydrophobic alkyl chains, each of which is surrounded by a layer of highly ordered water molecules. (b) By clustering together in micelles, the fatty acid molecules expose the smallest possible hydrophobic surface area to the water, and fewer water molecules are required in the shell of ordered water. The entropy gained by freeing immobilized water molecules stabilizes the micelle.
Many biomolecules are amphipathic; proteins, pigments, certain vitamins, and the sterols and phospholipids of membranes all have both polar and nonpolar surface regions. Structures composed of these molecules are stabilized by the hydrophobic effect, which favors aggregation of the nonpolar regions. The hydrophobic effect on interactions among lipids, and between lipids and proteins, is the most important determinant of structure in biological membranes. The aggregation of nonpolar amino acids in protein interiors, driven by the hydrophobic effect, also stabilizes the three-dimensional structures of proteins.
Hydrogen bonding between water and polar solutes also causes an ordering of water molecules, but the energetic effect is less significant than with nonpolar solutes. Disruption of ordered water molecules is part of the driving force for binding of a polar substrate (reactant) to the complementary polar surface of an enzyme: entropy increases as the enzyme displaces ordered water from the substrate and as the substrate displaces ordered water from the enzyme surface (Fig. 2-8). This topic is discussed in greater depth in Chapter 6 (p. 185).
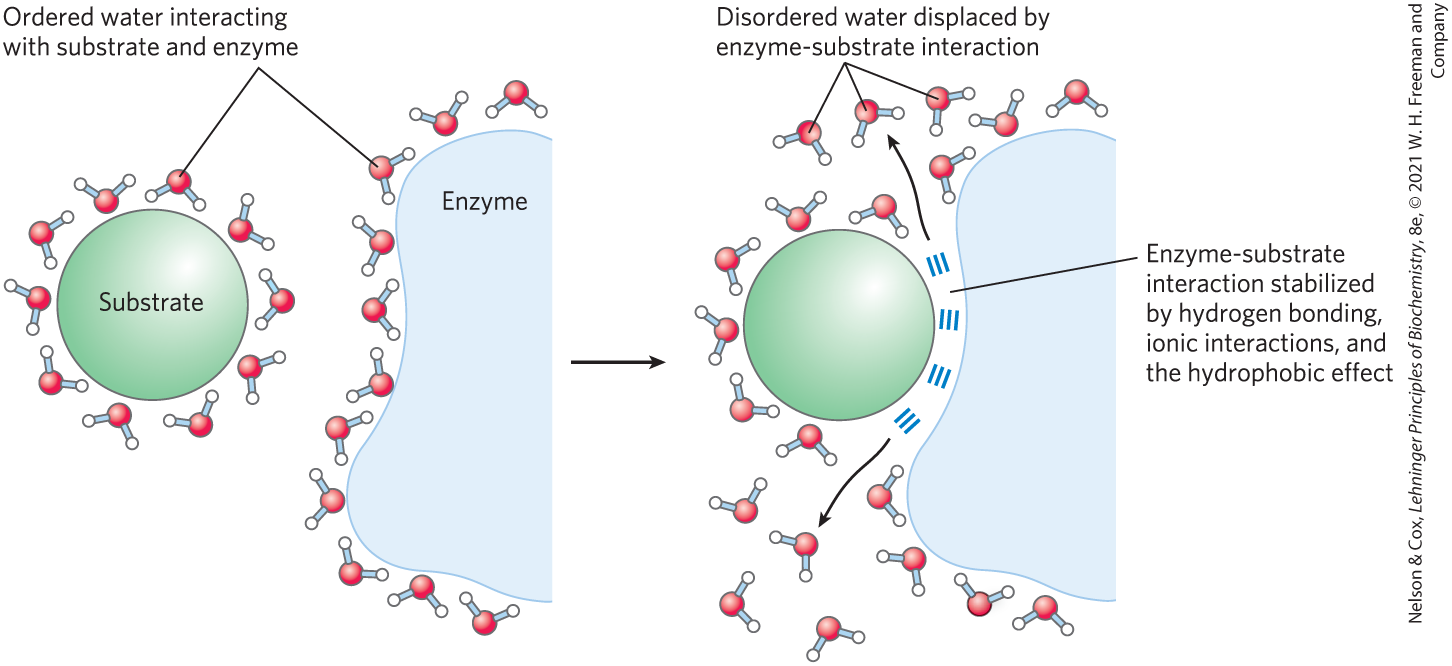
FIGURE 2-8 Release of ordered water favors formation of an enzyme-substrate complex. While separate, both enzyme and substrate force neighboring water molecules into an ordered shell. Binding of substrate to enzyme releases some of the ordered water, and the resulting increase in entropy provides a thermodynamic push toward formation of the enzyme-substrate complex.
van der Waals Interactions Are Weak Interatomic Attractions
When two uncharged atoms are brought very close together, their surrounding electron clouds influence each other. Random variations in the positions of the electrons around one nucleus may create a transient electric dipole, which induces a transient, opposite electric dipole in the nearby atom. The two dipoles weakly attract each other, bringing the two nuclei closer. These weak attractions are called van der Waals interactions (also known as London dispersion forces). As the two nuclei draw closer together, their electron clouds begin to repel each other. At the point where the net attraction is maximal, the nuclei are said to be in van der Waals contact. Each atom has a characteristic van der Waals radius, a measure of how close that atom will allow another to approach (Table 2-3). In the space-filling molecular models shown throughout this book, the atoms are depicted in sizes proportional to their van der Waals radii.
| Element | van der Waals radius (nm) | Covalent radius for single bond (nm) |
|---|---|---|
H |
0.11 |
0.030 |
O |
0.15 |
0.066 |
N |
0.15 |
0.070 |
C |
0.17 |
0.077 |
S |
0.18 |
0.104 |
P |
0.19 |
0.110 |
I |
0.21 |
0.133 |
|
Sources: For van der Waals radii, R. Chauvin, J. Phys. Chem. 96:9194, 1992. For covalent radii, L. Pauling, Nature of the Chemical Bond, 3rd edn, Cornell University Press, 1960. Note: van der Waals radii describe the space-filling dimensions of atoms. When two atoms are joined covalently, the atomic radii at the point of bonding are shorter than the van der Waals radii, because the joined atoms are pulled together by the shared electron pair. The distance between nuclei in a van der Waals interaction or a covalent bond is about equal to the sum of the van der Waals or covalent radii, respectively, for the two atoms. Thus, the length of a carbon-carbon single bond is about 0.077 nm + 0.077 nm = 0.154 nm. |
||
Weak Interactions Are Crucial to Macromolecular Structure and Function
I believe that as the methods of structural chemistry are further applied to physiological problems, it will be found that the significance of the hydrogen bond for physiology is greater than that of any other single structural feature.
—Linus Pauling, The Nature of the Chemical Bond, 1939
The noncovalent interactions we have described—hydrogen bonds and ionic, hydrophobic, and van der Waals interactions (Table 2-4)—are much weaker than covalent bonds. An input of about 350 kJ of energy is required to break a mole of single bonds, and about 410 kJ is needed to break a mole of bonds, but as little as 4 kJ is sufficient to disrupt a mole of typical van der Waals interactions. Interactions driven by the hydrophobic effect are also much weaker than covalent bonds, although they are substantially strengthened by a highly polar solvent (a concentrated salt solution, for example). Ionic interactions and hydrogen bonds are variable in strength, depending on the polarity of the solvent and the alignment of the hydrogen-bonded atoms, but they are always significantly weaker than covalent bonds. In aqueous solvent at , the available thermal energy can be of the same order of magnitude as the strength of these weak interactions, and the interaction between solute and solvent (water) molecules is nearly as favorable as solute-solute interactions. Consequently, hydrogen bonds and ionic, hydrophobic, and van der Waals interactions are continually forming and breaking.
Hydrogen bonds |
|
Between neutral groups |

|
Between peptide bonds |

|
Ionic interactions |
|
Attraction |

|
Repulsion |

|
Hydrophobic effect |
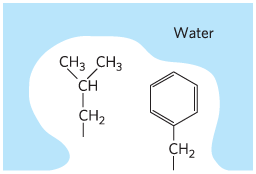
|
van der Waals interactions |
Any two atoms in close proximity |
Although these four types of interactions are individually weak relative to covalent bonds, the cumulative effect of many such interactions can be very significant. For example, the noncovalent binding of an enzyme to its substrate may involve several hydrogen bonds and one or more ionic interactions, as well as the hydrophobic effect and van der Waals interactions. The formation of each of these associations contributes to a net decrease in the free energy of the system. We can calculate the stability of a noncovalent interaction, such as the hydrogen bonding of a small molecule to its macromolecular partner, from the binding energy, the reduction in the energy of the system when binding occurs. Stability, as measured by the equilibrium constant (discussed in Section 2.2) of the binding reaction, varies exponentially with binding energy. To dissociate two biomolecules (such as an enzyme and its bound substrate) that are associated noncovalently through multiple weak interactions, all these interactions must be disrupted at the same time. Because the interactions fluctuate randomly, such simultaneous disruptions are very unlikely. Therefore, numerous weak interactions bestow much greater molecular stability than would be expected intuitively from a simple summation of small binding energies.
Macromolecules such as proteins, DNA, and RNA contain so many sites of potential hydrogen bonding or ionic, van der Waals, or hydrophobic clustering that the cumulative effect can be enormous. For macromolecules, the most stable (that is, the native) structure is usually that in which these weak interactions are maximized. The folding of a single polypeptide or polynucleotide chain into its three-dimensional shape is determined by this principle. The binding of an antigen to a specific antibody depends on the cumulative effects of many weak interactions. The energy released when an enzyme binds noncovalently to its substrate is the main source of the enzyme’s catalytic power. The binding of a hormone or a neurotransmitter to its cellular receptor protein is the result of multiple weak interactions. One consequence of the large size of enzymes and receptors (relative to their substrates or ligands) is that their extensive surfaces provide many opportunities for weak interactions. At the molecular level, the complementarity between interacting biomolecules reflects the complementarity and weak interactions between polar and charged groups and the proximity of hydrophobic patches on the surfaces of the molecules.
When the structure of a protein such as hemoglobin is determined by x-ray crystallography (see Fig. 4-30), water molecules are often found to be bound so tightly that they are part of the crystal structure (Fig. 2-9); the same is true for water in crystals of RNA or DNA. These bound water molecules, which can also be detected in aqueous solutions by nuclear magnetic resonance (see Fig. 4-31), have properties that are distinctly different from those of the “bulk” water of the solvent. For example, the bound water molecules are not osmotically active (see below). For many proteins, tightly bound water molecules are essential to their function. In a key reaction in photosynthesis, for example, protons flow across a biological membrane as light drives the flow of electrons through a series of electron-carrying proteins (see Fig. 20-17). One of these proteins, cytochrome f, has a chain of five bound water molecules (Fig. 2-10) that may provide a path for protons to move through the membrane by a process known as proton hopping (described later in this chapter).
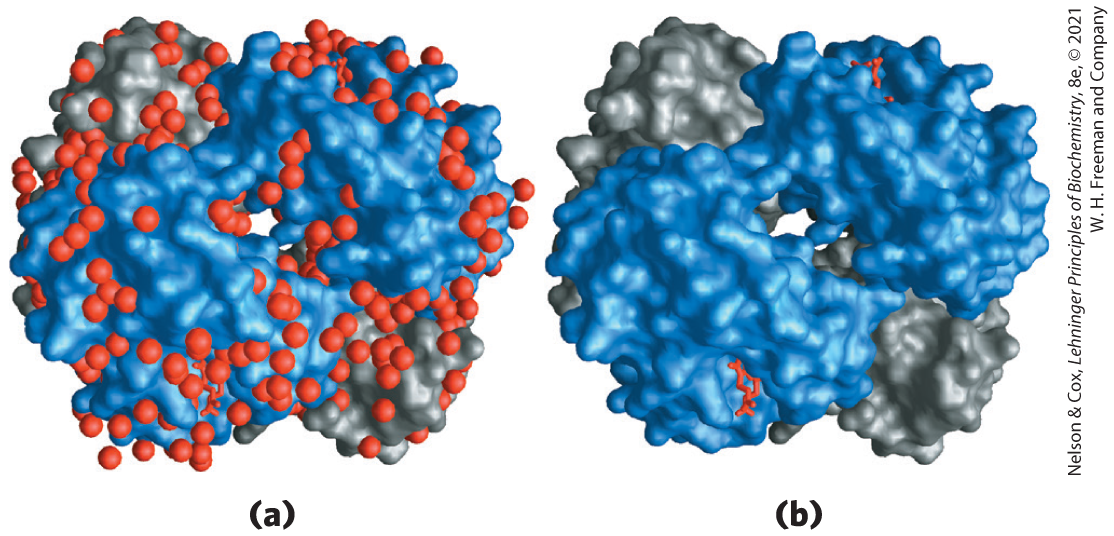
FIGURE 2-9 Water binding in hemoglobin. The crystal structure of hemoglobin, shown (a) with bound water molecules (red spheres) and (b) without the water molecules. The water molecules are so firmly bound to the protein that they affect the x-ray diffraction pattern as though they were fixed parts of the protein. The two α subunits of hemoglobin are shown in gray, the two β subunits in blue. Each subunit has a bound heme group (red stick structure), visible only in the β subunits in this view. The structure and function of hemoglobin are discussed in detail in Chapter 5. [Data from PDB ID 1A3N, J. R. H. Tame and B. Vallone, Acta Crystallogr. D 56:805, 2000.]
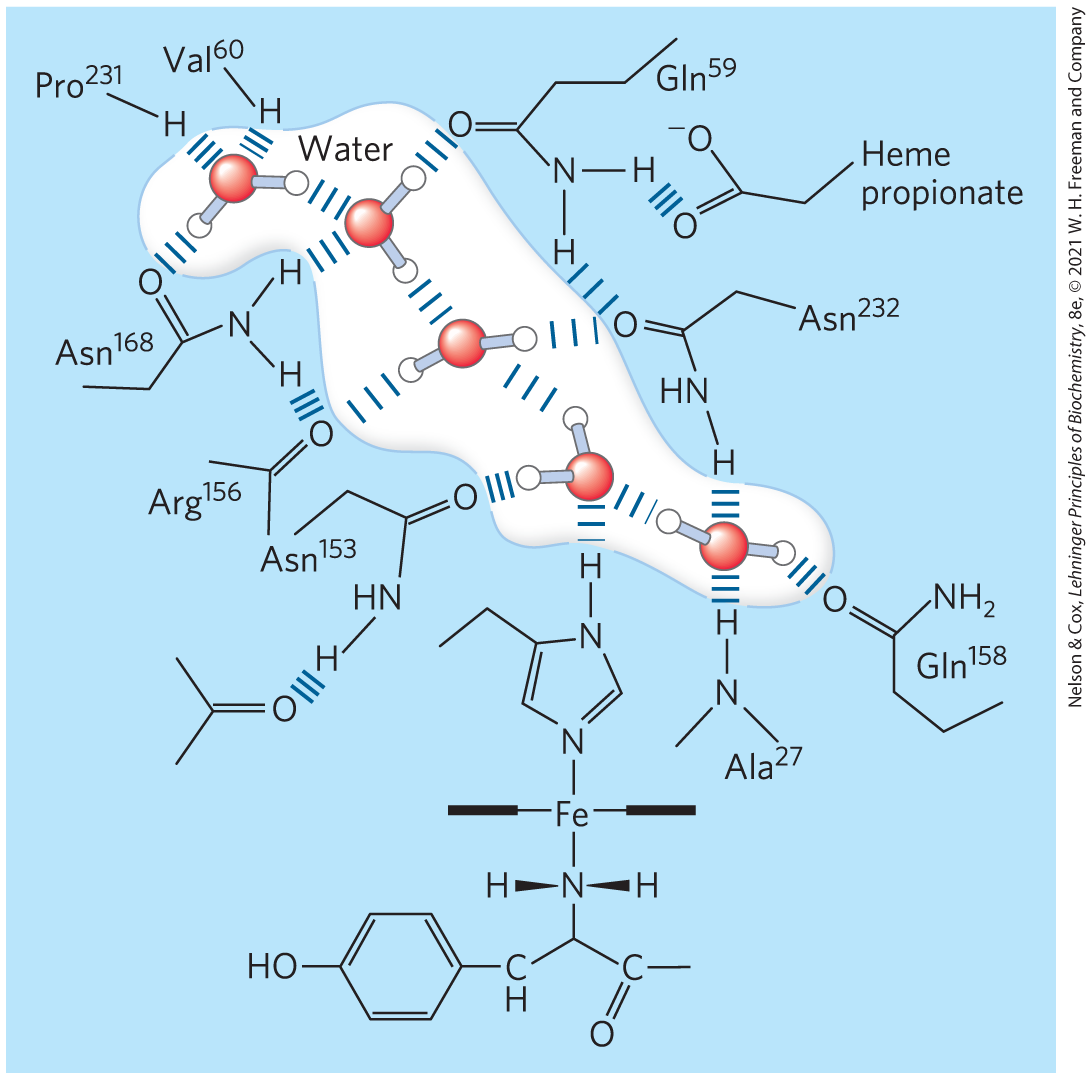
FIGURE 2-10 Water chain in cytochrome f. Water is bound in a proton channel of the membrane protein cytochrome f, which is part of the energy-trapping machinery of photosynthesis in chloroplasts. Five water molecules are hydrogen-bonded to each other and to functional groups of the protein: the peptide backbone atoms of valine, proline, arginine, and alanine residues, and the side chains of three asparagine and two glutamine residues. The protein has a bound heme, its iron ion facilitating electron flow during photosynthesis. Electron flow is coupled to the movement of protons across the membrane, which probably involves “proton hopping” through this chain of bound water molecules. [Information from P. Nicholls, Cell. Mol. Life Sci. 57:987, 2000, Fig. 6a (redrawn from PDB ID 1HCZ, S. E. Martinez et al., Prot. Sci. 5:1081, 1996).]
Concentrated Solutes Produce Osmotic Pressure
Solutes of all kinds alter certain physical properties of the solvent, water: its vapor pressure, its boiling point, its melting point (freezing point), and its osmotic pressure. These are called colligative properties (colligative meaning “tied together”), because the effect of solutes on all four properties has the same basis: the concentration of water is lower in solutions than in pure water. The effect of solute concentration on the colligative properties of water is independent of the chemical properties of the solute; it depends only on the number of solute particles (molecules or ions) in a given amount of water. For example, a compound such as NaCl, which dissociates in solution, has an effect on osmotic pressure that is twice that of an equal number of moles of a nondissociating solute such as glucose.
Water molecules tend to move from a region of higher water concentration to one of lower water concentration, in accordance with the tendency in nature for a system to become disordered. When two different aqueous solutions are separated by a semipermeable membrane (one that allows the passage of water but not solute molecules), water molecules diffusing from the region of higher water concentration to the region of lower water concentration produce osmotic pressure (Fig. 2-11). Osmotic pressure, Π, measured as the force necessary to resist water movement, is approximated by the van’t Hoff equation

FIGURE 2-11 Osmosis and the measurement of osmotic pressure. (a) The initial state. The tube contains an aqueous solution, the beaker contains pure water, and the semipermeable membrane allows the passage of water but not solute. Water flows from the beaker into the tube to equalize its concentration across the membrane. (b) The final state. Water has moved into the solution of the nonpermeant compound, diluting it and raising the column of solution within the tube. At equilibrium, the force of gravity operating on the solution in the tube exactly balances the tendency of water to move into the tube, where its concentration is lower. (c) Osmotic pressure (Π) is measured as the force that must be applied to return the solution in the tube to the level of the water in the beaker. This force is proportional to the height, h, of the column in (b).
in which R is the gas constant and T is the absolute temperature. The symbol i is the van’t Hoff factor, a measure of the extent to which the solute dissociates into two or more ionic species. The term c is the solute’s molar concentration, and ic is the osmolarity of the solution, the product of the van’t Hoff factor i and c. In dilute NaCl solutions, the solute completely dissociates into and , doubling the number of solute particles, and thus i = 2. For all nonionizing solutes, i = 1. For solutions of several (n) solutes, Π is the sum of the contributions of each species:
Osmosis, water movement across a semipermeable membrane driven by differences in osmotic pressure, is an important factor in the life of most cells. Plasma membranes are more permeable to water than to most other small molecules, ions, and macromolecules because protein channels (aquaporins; see Table 11-3) in the membrane selectively permit the passage of water. Solutions of osmolarity equal to that of a cell’s cytosol are said to be isotonic relative to that cell. Surrounded by an isotonic solution, a cell neither gains nor loses water (Fig. 2-12). In a hypertonic solution, one with higher osmolarity than that of the cytosol, the cell shrinks as water moves out. In a hypotonic solution, one with a lower osmolarity than the cytosol, the cell swells as water enters. In their natural environments, cells generally contain higher concentrations of biomolecules and ions than their surroundings, so osmotic pressure tends to drive water into cells. If not somehow counterbalanced, this inward movement of water would distend the plasma membrane and eventually cause bursting of the cell (osmotic lysis).
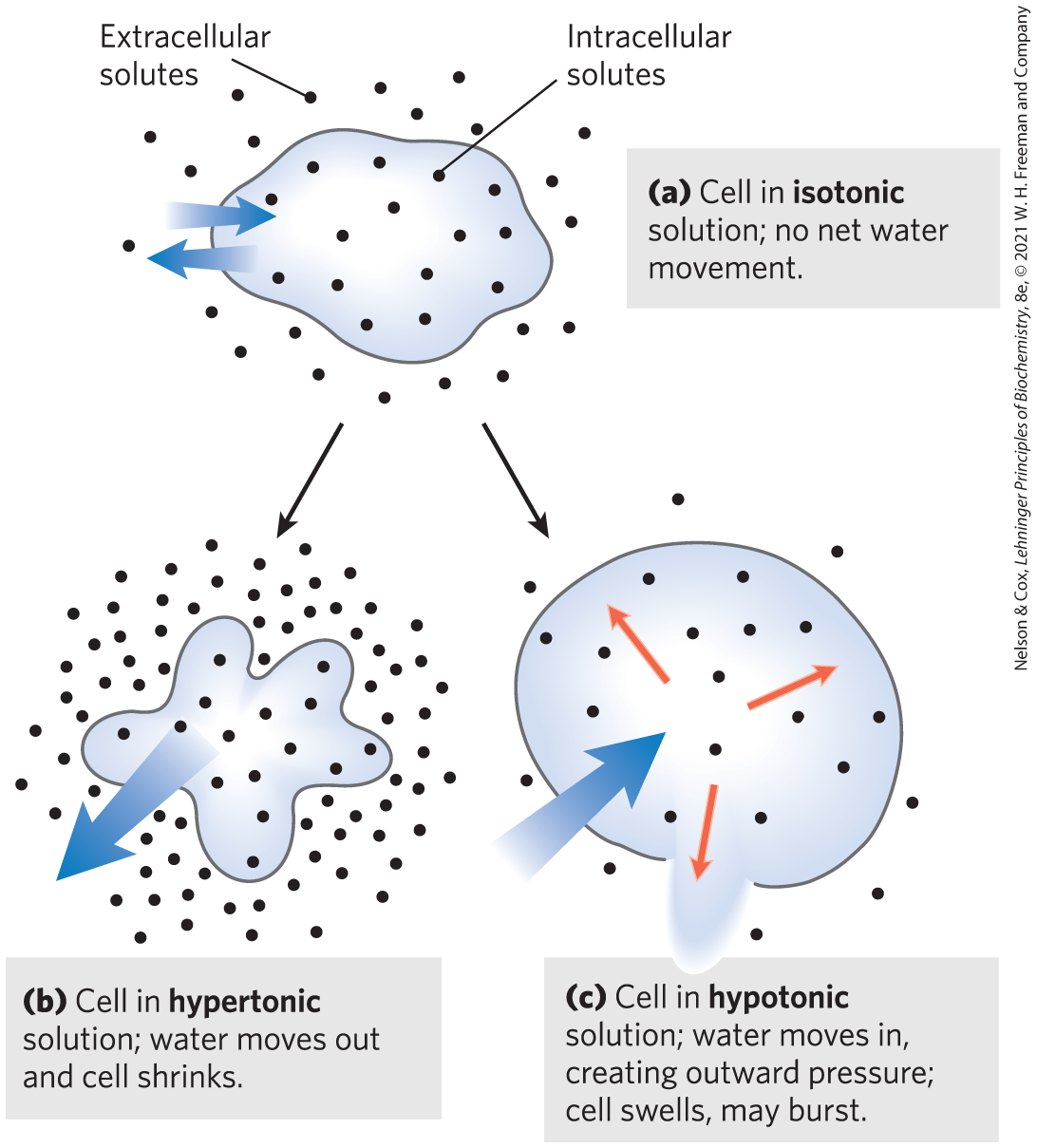
FIGURE 2-12 Effect of extracellular osmolarity on water movement across a plasma membrane. When a cell in osmotic balance with its surrounding medium—that is, a cell in (a) an isotonic medium—is transferred into (b) a hypertonic solution or (c) a hypotonic solution, water moves across the plasma membrane in the direction that tends to equalize osmolarity outside and inside the cell.
Several mechanisms have evolved to prevent this catastrophe. In bacteria and plants, the plasma membrane is surrounded by a nonexpandable cell wall of sufficient rigidity and strength to resist osmotic pressure and prevent osmotic lysis. Certain freshwater protists that live in a highly hypotonic medium have an organelle (contractile vacuole) that pumps water out of the cell. In multicellular animals, blood plasma and interstitial fluid (the extracellular fluid of tissues) are maintained at an osmolarity close to that of the cytosol. The high concentration of albumin and other proteins in blood plasma contributes to its osmolarity. Cells also actively pump out and other ions into the interstitial fluid to stay in osmotic balance with their surroundings.
Because the effect of solutes on osmolarity depends on the number of dissolved particles, not their mass, macromolecules (proteins, nucleic acids, polysaccharides) have far less effect on the osmolarity of a solution than an equal mass of their monomeric components would have. For example, a gram of a polysaccharide composed of 1,000 glucose units has about the same effect on osmolarity as a milligram of glucose. Storing fuel as polysaccharides (starch or glycogen) rather than as glucose or other simple sugars avoids an enormous increase in osmotic pressure in the storage cell.
Plants use osmotic pressure to achieve mechanical rigidity. The very high solute concentration in the plant cell vacuole draws water into the cell, but the nonexpandable cell wall prevents swelling; instead, the pressure exerted against the cell wall (turgor pressure) increases, stiffening the cell, the tissue, and the plant body. When the lettuce in your salad wilts, it is because loss of water has reduced turgor pressure. Osmosis also has consequences for laboratory protocols. Mitochondria, chloroplasts, and lysosomes, for example, are enclosed by semipermeable membranes. In isolating these organelles from broken cells, biochemists must perform the fractionations in isotonic solutions (see Fig. 1-7) to prevent excessive entry of water into the organelles and the swelling and bursting that would follow. Buffers used in cellular fractionations commonly contain sufficient concentrations of sucrose or some other inert solute to protect the organelles from osmotic lysis.
WORKED EXAMPLE 2-1 Osmotic Strength of an Organelle
Suppose the major solutes in intact lysosomes are KCl (∼0.1 m) and NaCl (∼0.03 m). When isolating lysosomes, what concentration of sucrose is required in the extracting solution at room temperature to prevent swelling and lysis?
SOLUTION:
We want to find a concentration of sucrose that gives an osmotic strength equal to that produced by the KCl and NaCl in the lysosomes. The equation for calculating osmotic strength (the van’t Hoff equation) is
where R is the gas constant 8.315 J/mol • K; T is the absolute temperature (Kelvin); , , and are the molar concentrations of each solute; and , , and are the numbers of particles each solute yields in solution (i = 2 for KCl and NaCl).
The osmotic strength of the lysosomal contents is
The osmotic strength of a sucrose solution is given by
In this case, , because sucrose does not ionize. Thus,
The osmotic strength of the lysosomal contents equals that of the sucrose solution when
Sucrose has a formula weight (FW) of 342, so the required sucrose concentration is (0.26 mol/L)(342 g/mol) = 88.92 g/L. Because the solute concentrations are accurate to only one significant figure, .
As we’ll see later (p. 242), cells of liver and muscle store carbohydrate not as low molecular weight sugars, such as glucose or sucrose, but as the high molecular weight polymer glycogen. This allows the cell to contain a large mass of glycogen with a minimal effect on the osmolarity of the cytosol.
SUMMARY 2.1 Weak Interactions in Aqueous Systems
- The very different electronegativities of H and O make water a highly polar molecule, capable of forming hydrogen bonds with itself and with solutes. Hydrogen bonds are fleeting, primarily electrostatic, and weaker than covalent bonds.
- Alcohols, aldehydes, ketones, and compounds containing bonds all form hydrogen bonds with water and are therefore water soluble.
- By screening the electrical charges of ions and by increasing the entropy of the system, water dissolves crystals of ionizable solutes.
- , , and are nonpolar and poorly soluble in water. and are ionizable and therefore very water soluble.
- Nonpolar (hydrophobic) compounds dissolve poorly in water; they cannot hydrogen-bond with the solvent, and their presence forces an energetically unfavorable ordering of water molecules at their hydrophobic surfaces. To minimize the surface exposed to water, nonpolar and amphipathic compounds such as lipids form aggregates (micelles and bilayer vesicles) in which the hydrophobic moieties are sequestered in the interior, an association driven by the hydrophobic effect, and only the more polar moieties interact with water.
- van der Waals interactions exist when two nearby nuclei induce dipoles in each other. The nearest approach of two atoms defines the van der Waals radius of each.
- Weak, noncovalent interactions, in large numbers, decisively influence the folding of macromolecules such as proteins and nucleic acids. The most stable macromolecular conformations are those in which hydrogen bonding is maximized within the molecule and between the molecule and the solvent, and in which hydrophobic moieties cluster in the interior of the molecule away from the aqueous solvent.
- When two aqueous compartments are separated by a semipermeable membrane (such as the plasma membrane separating a cell from its surroundings), water moves across that membrane to equalize the osmolarity in the two compartments. This tendency for water to move across a semipermeable membrane produces the osmotic pressure.
 Polar biomolecules dissolve readily in water because they can replace water-water interactions with energetically favorable water-solute interactions. In contrast, nonpolar biomolecules are poorly soluble in water because they interfere with water-water interactions but are unable to form water-solute interactions. In aqueous solutions, nonpolar molecules tend to cluster together.
Polar biomolecules dissolve readily in water because they can replace water-water interactions with energetically favorable water-solute interactions. In contrast, nonpolar biomolecules are poorly soluble in water because they interfere with water-water interactions but are unable to form water-solute interactions. In aqueous solutions, nonpolar molecules tend to cluster together.  Hydrogen bonds and ionic, hydrophobic (from the Greek, meaning “water-fearing”), and van der Waals interactions are individually weak, but collectively they have a very significant influence on the three-dimensional structures of proteins, nucleic acids, polysaccharides, and membrane lipids.
Hydrogen bonds and ionic, hydrophobic (from the Greek, meaning “water-fearing”), and van der Waals interactions are individually weak, but collectively they have a very significant influence on the three-dimensional structures of proteins, nucleic acids, polysaccharides, and membrane lipids. The very different electronegativities of H and O make water a highly polar molecule, capable of forming hydrogen bonds with itself and with solutes. Hydrogen bonds are fleeting, primarily electrostatic, and weaker than covalent bonds.
The very different electronegativities of H and O make water a highly polar molecule, capable of forming hydrogen bonds with itself and with solutes. Hydrogen bonds are fleeting, primarily electrostatic, and weaker than covalent bonds.