13.1 Bioenergetics and Thermodynamics in Chapter 13 Introduction to Metabolism

13.1 Bioenergetics and Thermodynamics

Bioenergetics is the quantitative study of energy transductions — changes of one form of energy into another — that occur in living cells, and of the nature and function of the chemical processes underlying these transductions. Although many of the principles of thermodynamics have been introduced in earlier chapters and may be familiar to you, a review of the quantitative aspects of these principles is useful here.

Biological Energy Transformations Obey the Laws of Thermodynamics

Many quantitative observations made by physicists and chemists on the interconversion of different forms of energy led, in the nineteenth century, to the formulation of two fundamental laws of thermodynamics. The first law is the principle of the conservation of energy: for any physical or chemical change, the total amount of energy in the universe remains constant; energy may change form or it may be transported from one region to another, but it cannot be created or destroyed. The second law of thermodynamics, which can be stated in several forms, says that the universe always tends toward increasing disorder: in all natural processes, the entropy of the universe increases.

A cartoon shows a man sitting in a chair holding a book titled Facts of Life and speaking to a boy sitting on his knees. Text reads, “Now, in the italicized second end italics law of thermodynamics…” A bookcase and a lamp are in the background.

Living organisms consist of collections of molecules much more highly organized than the surrounding materials from which they are constructed, and organisms maintain and produce order, seemingly immune to the second law of thermodynamics. But living organisms do not violate the second law; they operate strictly within it. To discuss the application of the second law to biological systems, we must first define those systems and their surroundings.

The reacting system is the collection of matter that is undergoing a particular chemical or physical process; it may be an organism, a cell, or two reacting compounds. The reacting system and its surroundings together constitute the universe. In the laboratory, some chemical or physical processes can be carried out in isolated or closed systems, in which no material or energy is exchanged with the surroundings. Living cells and organisms, however, are open systems, exchanging both material and energy with their surroundings; living systems are never at equilibrium with their surroundings, and the constant transactions between system and surroundings explain how organisms can create order within themselves while operating within the second law of thermodynamics.

In Chapter 1 (p. 21) we defined three thermodynamic quantities that describe the energy changes occurring in a chemical reaction:

Free energy, G (for J. Willard Gibbs), expresses the amount of energy capable of doing work during a reaction at constant temperature and pressure. When a reaction proceeds with the release of free energy (that is, when the system changes so as to possess less free energy), the free-energy change, ∆G, has a negative value and the reaction is said to be exergonic. In endergonic reactions, the system gains free energy and ∆G is positive.

Enthalpy, H, is the heat content of the reacting system. It reflects the number and kinds of chemical bonds (covalent and noncovalent) in the reactants and products. When a chemical reaction releases heat, it is said to be exothermic; the heat content of the products is less than that of the reactants, and the change in enthalpy, ∆H, has, by convention, a negative value. Reacting systems that take up heat from their surroundings are endothermic and have positive values of ∆H.

Entropy, S, is a quantitative expression for the randomness or disorder in a system (see Box 1-3). When the products of a reacting system are less complex and more disordered than the reactants, the reaction is said to proceed with a gain in entropy.

The units of ∆G and ∆H are joules/mole or calories/mole (recall that 1 cal $= 4.184 J$ $equals 4.184 upper J$ ); units of entropy are joules/mole • Kelvin $(J/mol • K)$ $left-parenthesis upper J slash mol bullet upper K right-parenthesis$ (Table 13-1).

TABLE 13-1 Some Physical Constants and Units Used in Thermodynamics
Boltzmann constant, $k = 1.381 \times 10^{- 23} J/K$ $bold k equals 1.381 times 10 Superscript negative 23 Baseline upper J slash upper K$ Avogadro’s number, $N = 6.022 \times 10^{23} {mol}^{- 1}$ $upper N equals 6.022 times 10 Superscript 23 Baseline mol Superscript negative 1$ Faraday constant, $F = 96,480 J/V • mol$ $upper F equals 96,480 upper J slash upper V bullet mol$ Gas constant, $R = 8.315 J/mol • K$ $upper R equals 8.315 upper J slash mol bullet upper K$ $(= 1.987 cal/mol • K)$ $left-parenthesis equals 1.987 cal slash mol bullet upper K right-parenthesis$
Units of ∆G and ∆H are J/mol (or cal/mol) Units of ∆S are J/mol • K (or cal/mol • K) $1 cal = 4.184 J$ $1 cal equals 4.184 upper J$
Units of absolute temperature, T, are Kelvin, K $25 ° C = 298 K$ $25 degree upper C equals 298 upper K$ At 25 °C, $R T = 2.478 kJ/mol$ $upper R upper T equals 2.478 kJ slash mol$ $(= 0.592 kcal/mol)$ $left-parenthesis equals 0.592 kcal slash mol right-parenthesis$

Under the conditions existing in biological systems (including constant temperature and pressure), changes in free energy, enthalpy, and entropy are related to each other quantitatively by the equation

Δ G = Δ H - T Δ S

$upper Delta upper G equals upper Delta upper H minus upper T upper Delta upper S$

(13-1)

in which ∆G is the change in Gibbs free energy of the reacting system, ∆H is the change in enthalpy of the system, T is the absolute temperature, and ∆S is the change in entropy of the system. By convention, ∆S has a positive sign when entropy increases and ∆H, as noted above, has a negative sign when heat is released by the system to its surroundings. Either of these conditions, both of which are typical of energetically favorable processes, tends to make ∆G negative. In fact, ∆G of a spontaneously reacting system is always negative.

The second law of thermodynamics states that the entropy of the universe increases during all chemical and physical processes, but it does not require that the entropy increase take place in the reacting system itself. The order produced within cells as they grow and divide is more than compensated for by the disorder they create in their surroundings in the course of growth and division (see Box 1-3, case 2). In short, living organisms preserve their internal order by taking from their surroundings free energy in the form of nutrients or sunlight, and returning to their surroundings an equal amount of energy as heat and entropy.

Cells are isothermal systems — they function at essentially constant temperature (and also function at constant pressure). Heat flow is not a source of energy for cells, because heat can do work only as it passes to a zone or an object at a lower temperature. The energy that cells can and must use is free energy, described by the Gibbs free-energy function G, which allows prediction of the direction of chemical reactions, their exact equilibrium position, and the amount of work they can (in theory) perform at constant temperature and pressure. Heterotrophic cells acquire free energy from nutrient molecules, and photosynthetic cells acquire it from absorbed solar radiation. Both kinds of cells transform this free energy into ATP and other energy-rich compounds capable of providing energy for biological work at constant temperature.

Standard Free-Energy Change Is Directly Related to the Equilibrium Constant

The composition of a reacting system (a mixture of chemical reactants and products) tends to continue changing until equilibrium is reached. (In the case of an organism, equilibrium is reached only after death and complete decay.) At the equilibrium concentration of reactants and products, the rates of the forward and reverse reactions are exactly equal and no further net change occurs in the system. The concentrations of reactants and products at equilibrium define the equilibrium constant, $K_{eq}$ $upper K Subscript eq$ (p. 23). In the general reaction

a A + b B ⇌ c C + d D

$a upper A plus b upper B right harpoon over left harpoon c upper C plus d upper D$

where a, b, c, and d are the number of molecules of A, B, C, and D participating, the equilibrium constant is given by

K_{eq} = \frac{[C]_{eq}^{c} [D]_{eq}^{d}}{[A]_{eq}^{a} [B]_{eq}^{b}}

$upper K Subscript eq Baseline equals StartFraction left-bracket upper C right-bracket Subscript eq Superscript c Baseline left-bracket upper D right-bracket Subscript eq Superscript d Baseline Over left-bracket upper A right-bracket Subscript eq Superscript a Baseline left-bracket upper B right-bracket Subscript eq Superscript b Baseline EndFraction$

(13-2)

where $[A]_{eq}, [B]_{eq}, [C]_{eq}, and [D]_{eq}$ $left-bracket upper A right-bracket Subscript eq Baseline comma left-bracket upper B right-bracket Subscript eq Baseline comma left-bracket upper C right-bracket Subscript eq Baseline comma and left-bracket upper D right-bracket Subscript eq Baseline$ are the molar concentrations of the reaction components at the point of equilibrium.

When a reacting system is not at equilibrium, the tendency to move toward equilibrium represents a driving force, the magnitude of which can be expressed as the free-energy change for the reaction, ∆G. Under standard conditions of temperature and pressure and when reactants and products are initially present at 1 m concentrations or, for gases, at partial pressures of 101.3 kilopascals (kPa), or 1 atm, the force driving the system toward equilibrium is defined as the standard free-energy change, $Δ G °$ $upper Delta upper G degree$ . By this definition, the standard state for reactions that involve hydrogen ions is $[H^{+}] = 1 M$ $left-bracket upper H Superscript plus Baseline right-bracket equals 1 upper M$ , or pH 0. Most biochemical reactions, however, occur in well-buffered aqueous solutions near pH 7; both the pH and the concentration of water (55.5 m) are essentially constant.

Key convention

For convenience of calculations, biochemists define a different standard state from that used in chemistry and physics: in the biochemical standard state, $[H^{+}]$ $left-bracket upper H Superscript plus Baseline right-bracket$ is $10^{- 7} M$ $10 Superscript negative 7 Baseline upper M$ (pH 7) and $[H_{2} O]$ $left-bracket upper H Subscript 2 Baseline upper O right-bracket$ is 55.5 m. For reactions that involve ${Mg}^{2 +}$ $Mg Superscript 2 plus$ (which include most of those with ATP as a reactant), $[{Mg}^{2 +}]$ $left-bracket Mg Superscript 2 plus Baseline right-bracket$ in solution is commonly taken to be constant at 1 mm.

Physical constants based on this biochemical standard state are called standard transformed constants and are written with a prime (such as $Δ G^{'} °$ $upper Delta upper G prime degree$ and $K_{eq}^{'}$ $upper K prime Subscript eq$ ) to distinguish them from the untransformed constants used by chemists and physicists. (Note that most other textbooks use the symbol $Δ G °^{'}$ $upper Delta upper G degree prime$ rather than $Δ G^{'} ° .$ $upper Delta upper G Superscript prime Baseline degree period$ Our use of $Δ G^{'} °$ $upper Delta upper G prime degree$ , recommended by an international committee of chemists and biochemists, is intended to emphasize that the transformed free-energy change, $Δ G^{'} °$ $upper Delta upper G prime degree$ , is the criterion for equilibrium.) For simplicity, we will hereafter refer to these transformed constants as standard free-energy changes and standard equilibrium constants.

Key convention

In another simplifying convention used by biochemists, when $H_{2} O$ $upper H Subscript 2 Baseline upper O$ , $H^{+}$ $upper H Superscript plus$ , and/or ${Mg}^{2 +}$ $Mg Superscript 2 plus$ are reactants or products, their concentrations are not included in equations such as Equation 13-2 but are instead incorporated into the constants $K_{eq}^{'}$ $upper K prime Subscript eq$ and $Δ G^{'} °$ $upper Delta upper G prime degree$ .

Just as $K_{eq}^{'}$ $upper K prime Subscript eq$ is a physical constant characteristic for each reaction, so too is $Δ G^{'} °$ $upper Delta upper G prime degree$ a constant. As we noted in Chapter 6, there is a simple relationship between $K_{eq}^{'}$ $upper K prime Subscript eq$ and $Δ G^{'} °$ $upper Delta upper G prime degree$ :

Δ G^{'} ° = - R T ln K_{eq}^{'}

$upper Delta upper G Superscript prime Baseline degree equals minus upper R upper T ln upper K prime Subscript eq$

(13-3)

The standard free-energy change of a chemical reaction is simply an alternative mathematical way of expressing its equilibrium constant. Table 13-2 shows the relationship between $Δ G^{'} °$ $upper Delta upper G prime degree$ and $K_{eq}^{'}$ $upper K prime Subscript eq$ . If the equilibrium constant for a given chemical reaction is 1.0, the standard free-energy change of that reaction is 0.0 (the natural logarithm of 1.0 is zero). If $K_{eq}^{'}$ $upper K prime Subscript eq$ of a reaction is greater than 1.0, its $Δ G^{'} °$ $upper Delta upper G prime degree$ is negative. If $K_{eq}^{'}$ $upper K prime Subscript eq$ is less than 1.0, $Δ G^{'} °$ $upper Delta upper G prime degree$ is positive. Because the relationship between $Δ G^{'} °$ $upper Delta upper G prime degree$ and $K_{eq}^{'}$ $upper K prime Subscript eq$ is exponential, relatively small changes in $Δ G^{'} °$ $upper Delta upper G prime degree$ correspond to large changes in $K_{eq}^{'}$ $upper K prime Subscript eq$ .

TABLE 13-2 Relationship between Equilibrium Constants and Standard Free-Energy Changes of Chemical Reactions
$K_{eq}^{'}$ $bold-italic upper K prime Subscript eq$	(kJ/mol)	(kcal/mol)^a
	$Δ G^{'} °$ $bold upper Delta bold-italic upper G prime degree$
$10^{3}$ $10 cubed$	$- 17.1$ $negative 17.1$	$- 4.1$ $negative 4.1$
$10^{2}$ $10 squared$	$- 11.4$ $negative 11.4$	$- 2.7$ $negative 2.7$
$10^{1}$ $10 Superscript 1$	$- 5.7$ $negative 5.7$	$- 1.4$ $negative 1.4$
1	0.0	0.0
$10^{- 1}$ $10 Superscript negative 1$	5.7	1.4
$10^{- 2}$ $10 Superscript negative 2$	11.4	2.7
$10^{- 3}$ $10 Superscript negative 3$	17.1	4.1
$10^{- 4}$ $10 Superscript negative 4$	22.8	5.5
$10^{- 5}$ $10 Superscript negative 5$	28.5	6.8
$10^{- 6}$ $10 Superscript negative 6$	34.2	8.2
^a Although joules and kilojoules are the standard units of energy and are used throughout this text, biochemists and nutritionists sometimes express $Δ G^{'} °$ $upper Delta upper G prime degree$ values in kilocalories per mole. We have therefore included values in both kilojoules and kilocalories in this table and in Tables 13-4 and 13-6. To convert kilojoules to kilocalories, divide the number of kilojoules by 4.184.

It may be helpful to think of the standard free-energy change in another way. $Δ G^{'} °$ $upper Delta upper G prime degree$ is the difference between the free-energy content of the products and the free-energy content of the reactants, under standard conditions. When $Δ G^{'} °$ $upper Delta upper G prime degree$ is negative, the products contain less free energy than the reactants and the reaction will proceed spontaneously under standard conditions; all chemical reactions tend to go in the direction that results in a decrease in the free energy of the system. A positive value of $Δ G^{'} °$ $upper Delta upper G prime degree$ means that the products of the reaction contain more free energy than the reactants, and this reaction will tend to go in the reverse direction if we start with 1.0 m concentrations of all components (standard conditions). Table 13-3 summarizes these points.

TABLE 13-3 Relationships among $bold-italic upper K bold prime Subscript bold eq$ $bold-italic upper K bold prime Subscript bold eq$ , $bold upper Delta bold-italic upper G bold prime degree$ $bold upper Delta bold-italic upper G bold prime degree$ , and the Direction of Chemical Reactions
When $K_{eq}^{'}$ $bold-italic upper K bold prime Subscript bold eq$ is …	$Δ G^{'} °$ $bold upper Delta bold-italic upper G bold prime degree$ is …	Starting with all components at 1 m, the reaction …
>1.0	negative	proceeds forward
1.0	zero	is at equilibrium
<1.0	positive	proceeds in reverse

WORKED EXAMPLE 13-1 Calculation of $Δ G^{'} °$ $bold upper Delta bold-italic upper G bold prime degree$

Calculate the standard free-energy change of the reaction catalyzed by the enzyme phosphoglucomutase,

Glucose 1 -phosphate ⇌ glucose 6 -phosphate

$Glucose 1 hyphen phosphate right harpoon over left harpoon glucose 6 hyphen phosphate$

given that, starting with 20 mm glucose 1-phosphate and no glucose 6-phosphate, the final equilibrium mixture at $25 ° C$ $25 degree upper C$ and pH 7.0 contains 1.0 mm glucose 1-phosphate and 19 mm glucose 6-phosphate. Does the reaction in the direction of glucose 6-phosphate formation proceed with a loss or a gain of free energy?

SOLUTION:

First we calculate the equilibrium constant:

K_{eq}^{'} = \frac{[glucose 6 -phosphate]_{eq}}{{[glucose 1 -phosphate]}_{eq}} = \frac{19 m M}{1.0 m M} = 19

$upper K prime Subscript eq Baseline equals StartFraction left-bracket glucose 6 hyphen phosphate right-bracket Subscript eq Baseline Over left-bracket glucose 1 hyphen phosphate right-bracket Subscript eq Baseline EndFraction equals StartFraction 19 m upper M Over 1.0 m upper M EndFraction equals 19$

We can now calculate the standard free-energy change:

\begin{matrix} Δ G^{'} ° & = & - R T ln K_{eq}^{'} \\ = & - (8.315 J/mol • K) (298 K) (ln 19) \\ = & - 7.3 kJ/mol \end{matrix}

$StartLayout 1st Row 1st Column upper Delta upper G Superscript prime Baseline degree 2nd Column equals 3rd Column minus upper R upper T ln upper K prime Subscript eq 2nd Row 1st Column Blank 2nd Column equals 3rd Column minus left-parenthesis 8.315 upper J slash mol bullet upper K right-parenthesis left-parenthesis 298 upper K right-parenthesis left-parenthesis ln 19 right-parenthesis 3rd Row 1st Column Blank 2nd Column equals 3rd Column negative 7.3 kJ slash mol EndLayout$

Because the standard free-energy change is negative, the conversion of glucose 1-phosphate to glucose 6-phosphate proceeds with a loss (release) of free energy. (For the reverse reaction, $Δ G^{'} °$ $upper Delta upper G prime degree$ has the same magnitude but the opposite sign.)

Table 13-4 gives the standard free-energy changes for some representative chemical reactions. Note that hydrolysis of simple esters, amides, peptides, and glycosides, as well as rearrangements and eliminations, proceed with relatively small standard free-energy changes, whereas hydrolysis of acid anhydrides is accompanied by relatively large decreases in standard free energy. The complete oxidation of organic compounds such as glucose or palmitate to ${CO}_{2}$ $CO Subscript 2$ and $H_{2} O$ $upper H Subscript 2 Baseline upper O$ , which in cells requires many steps, results in very large decreases in standard free energy. However, standard free-energy changes such as those in Table 13-4 indicate how much free energy is available from a reaction under standard conditions. To describe the energy released under the conditions existing in cells, an expression for the actual free-energy change is essential.

TABLE 13-4 Standard Free-Energy Changes of Some Chemical Reactions
Reaction type	(kJ/mol)	(kcal/mol)
	$Δ G^{'} °$ $upper Delta bold-italic upper G prime degree$
Hydrolysis reactions
Acid anhydrides
$Acetic anhydride + H_{2} O \overset{}{\to} 2 acetate$ $Acetic anhydride plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts 2 acetate$	$- 91.1$ $negative 91.1$	$- 21.8$ $negative 21.8$
$ATP + H_{2} O \overset{}{\to} ADP + P_{i}$ $ATP plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts ADP plus upper P Subscript i Baseline$	$- 30.5$ $negative 30.5$	$- 7.3$ $negative 7.3$
$ATP + H_{2} O \overset{}{\to} AMP + {PP}_{i}$ $ATP plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts AMP plus PP Subscript i Baseline$	$- 45.6$ $negative 45.6$	$- 10.9$ $negative 10.9$
${PP}_{i} + H_{2} O \overset{}{\to} 2 P_{i}$ $PP Subscript i Baseline plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts 2 upper P Subscript i Baseline$	$- 19.2$ $negative 19.2$	$- 4.6$ $negative 4.6$
$UDP-glucose + H_{2} O \overset{}{\to} UMP + glucose 1 -phosphate$ $UDP hyphen glucose plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts UMP plus glucose 1 hyphen phosphate$	$- 43.0$ $negative 43.0$	$- 10.3$ $negative 10.3$
Esters
$Ethyl acetate + H_{2} O \overset{}{\to} ethanol + acetate$ $Ethyl acetate plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts ethanol plus acetate$	$- 19.6$ $negative 19.6$	$- 4.7$ $negative 4.7$
$Glucose 6 -phosphate + H_{2} O \overset{}{\to} glucose + P_{i}$ $Glucose 6 hyphen phosphate plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts glucose plus upper P Subscript i Baseline$	$- 13.8$ $negative 13.8$	$- 3.3$ $negative 3.3$
Amides and peptides
$Glutamine + H_{2} O \overset{}{\to} glutamate + {NH}_{4}^{+}$ $Glutamine plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts glutamate plus NH Subscript 4 Superscript plus$	$- 14.2$ $negative 14.2$	$- 3.4$ $negative 3.4$
$Glycylglycine + H_{2} O \overset{}{\to} 2 glycine$ $Glycylglycine plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts 2 glycine$	$- 9.2$ $negative 9.2$	$- 2.2$ $negative 2.2$
Glycosides
$Maltose + H_{2} O \overset{}{\to} 2 glucose$ $Maltose plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts 2 glucose$	$- 15.5$ $negative 15.5$	$- 3.7$ $negative 3.7$
$Lactose + H_{2} O \overset{}{\to} glucose + galactose$ $Lactose plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts glucose plus galactose$	$- 15.9$ $negative 15.9$	$- 3.8$ $negative 3.8$
Rearrangements
$Glucose 1 -phosphate \overset{}{\to} glucose 6 -phosphate$ $Glucose 1 hyphen phosphate right-arrow Overscript Endscripts glucose 6 hyphen phosphate$	$- 7.3$ $negative 7.3$	$- 1.7$ $negative 1.7$
$Fructose 6 -phosphate \overset{}{\to} glucose 6 -phosphate$ $Fructose 6 hyphen phosphate right-arrow Overscript Endscripts glucose 6 hyphen phosphate$	$- 1.7$ $negative 1.7$	$- 0.4$ $negative 0.4$
Elimination of water
$Malate \overset{}{\to} fumarate + H_{2} O$ $Malate right-arrow Overscript Endscripts fumarate plus upper H Subscript 2 Baseline upper O$	3.1	0.8
Oxidations with molecular oxygen
$Glucose + 6 O_{2} \overset{}{\to} 6 {CO}_{2} + 6 H_{2} O$ $Glucose plus 6 upper O Subscript 2 Baseline right-arrow Overscript Endscripts 6 CO Subscript 2 Baseline plus 6 upper H Subscript 2 Baseline upper O$	$- 2,840$ $negative 2,840$	$- 686$ $negative 686$
$Palmitate + 23 O_{2} \overset{}{\to} {16CO}_{2} + 16 H_{2} O$ $Palmitate plus 23 upper O Subscript 2 Baseline right-arrow Overscript Endscripts 16 CO Subscript 2 Baseline plus 16 upper H Subscript 2 Baseline upper O$	$- 9,770$ $negative 9,770$	$- 2,338$ $negative 2,338$

Actual Free-Energy Changes Depend on Reactant and Product Concentrations

We must be careful to distinguish between two different quantities: the actual free-energy change, ∆G, and the standard free-energy change, $Δ G^{'} ° .$ $upper Delta upper G Superscript prime Baseline degree period$ Each chemical reaction has a characteristic standard free-energy change, which may be positive, negative, or zero, depending on the equilibrium constant of the reaction. The standard free-energy change tells us in which direction and how far a given reaction must go to reach equilibrium when the initial concentration of each component is 1.0 m, the pH is 7.0, the temperature is $25 ° C$ $25 degree upper C$ , and the pressure is 101.3 kPa (1 atm). Thus $Δ G^{'} °$ $upper Delta upper G prime degree$ is a constant: it has a characteristic, unchanging value for a given reaction. But the actual free-energy change, ΔG, is a function of reactant and product concentrations and of the temperature prevailing during the reaction, none of which will necessarily match the standard conditions as defined above. Moreover, the ΔG of any reaction proceeding spontaneously toward its equilibrium is always negative, becomes less negative as the reaction proceeds, and is zero at the point of equilibrium, indicating that no more work can be done by the reaction.

ΔG and $Δ G^{'} °$ $upper Delta upper G prime degree$ for any reaction $a A + b B ⇌ c C + d D$ $a upper A plus b upper B right harpoon over left harpoon c upper C plus d upper D$ are related by the equation

An equation reads, Greek letter delta italicized G end italics equals Greek letter delta italicized G end italics prime degree sign plus a red highlighted part of italicized R T end italics l n [uppercase C] superscript italicized lowercase c end italics times [uppercase D] superscript italicized lowercase d end italics, both divided by the product of [uppercase A] superscript italicized lowercase a end italics and [uppercase B] superscript italicized lowercase b.

(13-4)

in which the terms in red are those actually prevailing in the system under observation. The concentration terms in this equation express the effects commonly called mass action, and the term ${[C]}^{c} {[D]}^{d} / {[A]}^{a} [B]^{b}$ $left-bracket upper C right-bracket Superscript c Baseline left-bracket upper D right-bracket Superscript d Baseline slash left-bracket upper A right-bracket Superscript a Baseline left-bracket upper B right-bracket Superscript b$ is called the mass-action ratio, Q. Thus Equation 13-4 can be expressed as $Δ G = Δ G^{'} ° + R T$ $upper Delta upper G equals upper Delta upper G prime degree plus upper R upper T$ ln Q. As an example, let us suppose that the reaction $A + B ⇌ C + D$ $upper A plus upper B right harpoon over left harpoon upper C plus upper D$ is taking place under the standard conditions of temperature $(25 ° C)$ $left-parenthesis 25 degree upper C right-parenthesis$ and pressure (101.3 kPa) but that the concentrations of A, B, C, and D are not equal and none of the components is present at the standard concentration of 1.0 m. To determine the actual free-energy change, ΔG, under these nonstandard conditions of concentration as the reaction proceeds from left to right, we simply enter the actual concentrations of A, B, C, and D in Equation 13-4; the values of R, T, and $Δ G^{'} °$ $upper Delta upper G prime degree$ are the standard values. ΔG is negative and approaches zero as the reaction proceeds, because the actual concentrations of A and B decrease and the concentrations of C and D increase. Notice that when a reaction is at equilibrium — when there is no force driving the reaction in either direction and ΔG is zero — Equation 13-4 reduces to

0 = Δ G = Δ G^{'} ° + R T ln \frac{{[C]}_{eq} {[D]}_{eq}}{{[A]}_{eq} {[B]}_{eq}}

$0 equals upper Delta upper G equals upper Delta upper G prime degree plus upper R upper T ln StartFraction left-bracket upper C right-bracket Subscript eq Baseline left-bracket upper D right-bracket Subscript eq Baseline Over left-bracket upper A right-bracket Subscript eq Baseline left-bracket upper B right-bracket Subscript eq Baseline EndFraction$

Δ G^{'} ° = - R T ln K_{eq}^{'}

$upper Delta upper G Superscript prime Baseline degree equals minus upper R upper T ln upper K prime Subscript eq$

which is the equation relating the standard free-energy change and equilibrium constant (Eqn 13-3).

The criterion for spontaneity of a reaction is the value of ΔG, not $Δ G^{'} °$ $upper Delta upper G prime degree$ . A reaction with a positive $Δ G^{'} °$ $upper Delta upper G prime degree$ can go in the forward direction if ΔG is negative. This is possible if the term RT ln ([products]/[reactants]) in Equation 13-4 is negative and has a larger absolute value than $Δ G^{'} °$ $upper Delta upper G prime degree$ . For example, the immediate removal of the products of a reaction by an enzyme that degrades the product can keep the ratio [products]/[reactants] well below 1, such that the term RT ln ([products]/[reactants]) has a large, negative value. This is a quantitative expression of Le Chatelier’s principle. $Δ G^{'} °$ $upper Delta upper G prime degree$ and ΔG are expressions of the maximum amount of free energy that a given reaction can theoretically deliver — an amount of energy that could be realized only if a perfectly efficient device were available to trap or harness it. Given that no such device is possible (some energy is always lost to entropy during any process), the amount of work done by the reaction at constant temperature and pressure is always less than the theoretical amount.

Another important point is that some thermodynamically favorable reactions (that is, reactions for which $Δ G^{'} °$ $upper Delta upper G prime degree$ is large and negative) do not occur at measurable rates. For example, combustion of firewood to ${CO}_{2}$ $CO Subscript 2$ and $H_{2} O$ $upper H Subscript 2 Baseline upper O$ is very favorable thermodynamically, but firewood remains stable for years because the activation energy (see Figs. 6-2, 6-3) for the combustion reaction is higher than the energy available at room temperature. If the necessary activation energy is provided (with a lighted match, for example), combustion will begin, converting the wood to the more stable products ${CO}_{2}$ $CO Subscript 2$ and $H_{2} O$ $upper H Subscript 2 Baseline upper O$ and releasing energy as heat and light. The heat released by this exothermic reaction provides the activation energy for combustion of neighboring regions of the firewood; the process is self-perpetuating. Thermodynamics allows us to predict which direction a process will tend to go; how fast it will go is the subject of kinetics.

In living cells, reactions that would be extremely slow if uncatalyzed are caused to proceed not by supplying additional heat but by lowering the activation energy through use of an enzyme catalyst. An enzyme provides an alternative reaction pathway with a lower activation energy than the uncatalyzed reaction, so that at body temperature a large fraction of the substrate molecules have enough thermal energy to overcome the activation barrier, and the reaction rate increases dramatically. The free-energy change for a reaction is independent of the pathway by which the reaction occurs; it depends only on the nature and concentration of the initial reactants and the final products. Enzymes cannot, therefore, change equilibrium constants; but they can and do increase the rate at which a reaction proceeds in the direction dictated by thermodynamics (see Section 6.2).

Standard Free-Energy Changes Are Additive

In the case of two sequential chemical reactions, $A ⇌ B$ $upper A right harpoon over left harpoon upper B$ and $B ⇌ C$ $upper B right harpoon over left harpoon upper C$ , each reaction has its own equilibrium constant and each has its characteristic standard free-energy change, $Δ G_{1}^{'} °$ $upper Delta upper G prime 1 degree$ and $Δ G_{2}^{'} °$ $upper Delta upper G prime 2 degree$ . As the two reactions are sequential, B cancels out to give the overall reaction $A ⇌ C$ $upper A right harpoon over left harpoon upper C$ , which has its own equilibrium constant and thus its own standard free-energy change, $Δ G_{Sum}^{'°}$ $upper Delta upper G Subscript Sum Superscript prime degree$ . The $Δ G^{'} °$ $upper Delta upper G prime degree$ values of sequential chemical reactions are additive. For the overall reaction $A ⇌ C$ $upper A right harpoon over left harpoon upper C$ , $Δ G_{Sum}^{'°}$ $upper Delta upper G Subscript Sum Superscript prime degree$ is the sum of the individual standard free-energy changes, $Δ G_{1}^{'} °$ $upper Delta upper G prime 1 degree$ and $Δ G_{2}^{'} °$ $upper Delta upper G prime 2 degree$ , of the two reactions: $Δ G_{Sum}^{'°} = Δ G_{1}^{'} ° + Δ G_{2}^{'} °$ $upper Delta upper G Subscript Sum Superscript prime degree Baseline equals upper Delta upper G prime 1 degree plus upper Delta upper G prime 2 degree$ .

A figure shows how two reactions can be added to produce the sum of the two reactions and to give the overall free energy change associated with the combination of reactions.

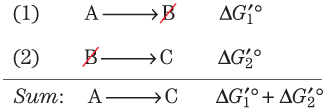
This principle of bioenergetics explains how a thermodynamically unfavorable (endergonic) reaction can be driven in the forward direction by coupling it to a highly exergonic reaction. For example, in many organisms, the synthesis of glucose 6-phosphate is the first step in the utilization of glucose. In principle, the synthesis could be accomplished by this reaction:

Glucose + P_{i} \overset{}{\to} {glucose 6-phosphate + H}_{2} O Δ G^{'} ° = 13.8 KJ/mol

$Glucose plus upper P Subscript i Baseline right-arrow Overscript Endscripts glucose 6 hyphen phosphate plus upper H Subscript 2 Baseline upper O upper Delta upper G prime degree equals 13.8 KJ slash mol$

But the positive value of $Δ G^{'} °$ $upper Delta upper G prime degree$ predicts that under standard conditions the reaction will tend not to proceed spontaneously in the direction written. Another cellular reaction, the hydrolysis of ATP to ADP and $P_{i}$ $upper P Subscript i$ , is highly exergonic:

ATP + H_{2} O \overset{}{\to} ADP + P_{i} Δ G^{'} ° = - 30.5 kJ/mol

$ATP plus upper H Subscript 2 Baseline upper O right-arrow Overscript Endscripts ADP plus upper P Subscript i Baseline upper Delta upper G Superscript prime Baseline degree equals negative 30.5 kJ slash mol$

These two reactions share the common intermediates $P_{i}$ $upper P Subscript i$ and $H_{2} O$ $upper H Subscript 2 Baseline upper O$ and may be expressed as sequential reactions:

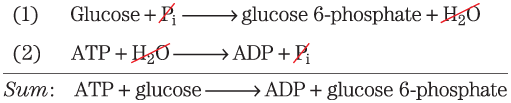
A figure shows how two reactions can be added to produce the sum of the two reactions, A T P plus glucose yields A D P plus glucose 6-phosphate.

The overall standard free-energy change is obtained by adding the $Δ G^{'} °$ $upper Delta upper G prime degree$ values for individual reactions:

Δ G_{Sum}^{'°} = 13.8 kJ/mol + (- 30.5 kJ/mol) = - 16.7 kJ/mol

$upper Delta upper G Subscript Sum Superscript prime degree Baseline equals 13.8 kJ slash mol plus left-parenthesis negative 30.5 kJ slash mol right-parenthesis equals negative 16.7 kJ slash mol$

The overall reaction is exergonic. In this case, energy stored in ATP is used to drive the synthesis of glucose 6-phosphate, even though its formation from glucose and inorganic phosphate $(P_{i})$ $left-parenthesis upper P Subscript i Baseline right-parenthesis$ is endergonic. The pathway of glucose 6-phosphate formation from glucose by phosphoryl transfer from ATP is different from reactions (1) and (2), but the net result is the same as the sum of the two reactions. The standard free-energy change is a state function. In thermodynamic calculations, all that matters is the state of the system at the beginning of the process and its state at the end; the route between the initial and final states is immaterial.

We have said that $Δ G^{'} °$ $upper Delta upper G prime degree$ is a way of expressing the equilibrium constant for a reaction. For reaction (1),

K_{eq1}^{'} = \frac{[glucose 6-phosphate]_{eq}}{[glucose]_{eq} [P_{i}]_{eq}} = 3.9 \times 10^{- 3} M^{- 1}

$upper K prime Subscript eq 1 Baseline equals StartFraction left-bracket glucose 6 hyphen phosphate right-bracket Subscript eq Baseline Over left-bracket glucose right-bracket Subscript eq Baseline left-bracket upper P Subscript i Baseline right-bracket Subscript eq Baseline EndFraction equals 3.9 times 10 Superscript negative 3 Baseline upper M Superscript negative 1$

Notice that $H_{2} O$ $upper H Subscript 2 Baseline upper O$ is not included in this expression, as its concentration (55.5 m) is assumed to remain unchanged by the reaction. The equilibrium constant for the hydrolysis of ATP is

K_{eq2}^{'} = \frac{[ADP]_{eq} [P_{i}]_{eq}}{[ATP]_{eq}} = 2.0 \times 10^{5} M

$upper K prime Subscript eq 2 Baseline equals StartFraction left-bracket ADP right-bracket Subscript eq Baseline left-bracket upper P Subscript i Baseline right-bracket Subscript eq Baseline Over left-bracket ATP right-bracket Subscript eq Baseline EndFraction equals 2.0 times 10 Superscript 5 Baseline upper M$

The equilibrium constant for the two coupled reactions is

\begin{array}{l} K_{{eq}_{3}}^{'} & = \frac{{[glucose6-phosphate]}_{eq} {[ADP]}_{eq} {[P_{i}]}_{eq}}{{[glucose]}_{eq} {[P_{i}]}_{eq} {[ATP]}_{eq}} \\ = (K_{{eq}_{1}}^{'}) (K_{{eq}_{2}}^{'}) = (3.9 \times 10^{- 3} M^{- 1}) (2.0 \times 10^{5} M) \\ = 7.8 \times 10^{2} \end{array}

$StartLayout 1st Row 1st Column upper K prime Subscript eq Sub Subscript 3 2nd Column equals StartFraction left-bracket glucose 6 hyphen phosphate right-bracket Subscript eq Baseline left-bracket ADP right-bracket Subscript eq Baseline left-bracket upper P Subscript i Baseline right-bracket Subscript eq Baseline Over left-bracket glucose right-bracket Subscript eq Baseline left-bracket upper P Subscript i Baseline right-bracket Subscript eq Baseline left-bracket ATP right-bracket Subscript eq Baseline EndFraction 2nd Row 1st Column Blank 2nd Column equals left-parenthesis upper K prime Subscript eq Sub Subscript 1 Subscript right-parenthesis left-parenthesis upper K prime Subscript eq Sub Subscript 2 Subscript right-parenthesis equals left-parenthesis 3.9 times 10 Superscript negative 3 Baseline upper M Superscript negative 1 Baseline right-parenthesis left-parenthesis 2.0 times 10 Superscript 5 Baseline upper M right-parenthesis 3rd Row 1st Column Blank 2nd Column equals 7 period 8 times 10 squared EndLayout$

This calculation illustrates an important point about equilibrium constants: although the $Δ G^{'} °$ $upper Delta upper G prime degree$ values for two reactions that sum to a third, overall reaction are additive, the $K_{eq}^{'}$ $upper K prime Subscript eq$ for the overall reaction is the product of the individual $K_{eq}^{'}$ $upper K prime Subscript eq$ values for the two reactions. Equilibrium constants are multiplicative. By coupling ATP hydrolysis to glucose 6-phosphate synthesis, the $K_{eq}^{'}$ $upper K prime Subscript eq$ for formation of glucose 6-phosphate from glucose has been raised by a factor of about $2 \times 10^{5}$ $2 times 10 Superscript 5$ compared with the direct reaction between glucose and $P_{i}$ $upper P Subscript i$ .

This strategy of coupling endergonic processes to exergonic reactions that drive them is employed by all living cells in the synthesis of metabolic intermediates and cellular components. Obviously, the strategy works only if compounds such as ATP are continuously available. In the following chapters we consider several of the most important cellular pathways for producing ATP. For more practice in dealing with free-energy changes and equilibrium constants for coupled reactions, see Worked Examples 1-1, 1-2, and 1-3 in Chapter 1 (pp. 24–25).

SUMMARY 13.1 Bioenergetics and Thermodynamics

Bioenergetics is the quantitative study of energy relationships and energy conversions in biological systems. Biological energy transformations obey the laws of thermodynamics.
Living cells constantly perform work. They require energy for maintaining their highly organized structures, synthesizing cellular components, transporting small molecules and ions across membranes, and generating electric currents.
All chemical reactions are influenced by two forces: the tendency to achieve the most stable bonding state (for which enthalpy, H, is a useful expression) and the tendency to achieve the highest degree of randomness, expressed as entropy, S. The driving force in a reaction is ΔG, the free-energy change, which represents the net effect of these two factors: $Δ G = Δ H - T Δ S$ $upper Delta upper G equals upper Delta upper H minus upper T upper Delta upper S$ .
The standard transformed free-energy change, $Δ G^{'} °$ $upper Delta upper G prime degree$ , is a physical constant that is characteristic for a given reaction and can be calculated from the equilibrium constant for the reaction: $Δ G^{'} ° = - R T ln K_{eq}^{'}$ $upper Delta upper G Superscript prime Baseline degree equals minus upper R upper T ln upper K prime Subscript eq$ .
The actual free-energy change, ΔG, is a variable that depends on $Δ G^{'} °$ $upper Delta upper G prime degree$ and on the concentrations of reactants and products: $Δ G = Δ G^{'} ° + R T ln$ $upper Delta upper G equals upper Delta upper G Superscript prime Baseline degree plus upper R upper T ln$ ([products]/[reactants]). When ΔG is large and negative, the reaction tends to go in the forward direction; when ΔG is large and positive, the reaction tends to go in the reverse direction; and when $Δ G = 0$ $upper Delta upper G equals 0$ , the system is at equilibrium.
The free-energy change for a reaction is independent of the pathway by which the reaction occurs. Free-energy changes are additive; the net chemical reaction that results from successive reactions sharing a common intermediate has an overall free-energy change that is the sum of the ΔG values for the individual reactions.