2.3 Buffering against pH Changes in Biological Systems in Chapter 2 Water, The Solvent Of Life

2.3 Buffering against pH Changes in Biological Systems

Almost every biological process is pH-dependent; a small change in pH produces a large change in the rate of the process. This is true not only for the many reactions in which the $mathml alt text514$ $upper H Superscript plus$ ion is a direct participant, but also for those reactions in which there is no apparent role for $mathml alt text515$ $upper H Superscript plus$ ions. The enzymes that catalyze cellular reactions, and many of the molecules on which they act, contain ionizable groups with characteristic $mathml alt text516$ $p upper K Subscript a Baseline$ values. The protonated amino and carboxyl groups of amino acids and the phosphate groups of nucleotides, for example, function as weak acids; their ionic state is determined by the pH of the surrounding medium. (When an ionizable group is sequestered in the middle of a protein, away from the aqueous solvent, its $mathml alt text518$ $p upper K Subscript a Baseline$ , or apparent $mathml alt text519$ $p upper K Subscript a Baseline$ , can be significantly different from its $mathml alt text520$ $p upper K Subscript a Baseline$ in water.) As we noted above, ionic interactions are among the forces that stabilize a protein molecule and allow an enzyme to recognize and bind to its substrate.

Cells and organisms maintain a specific and constant cytosolic pH, usually near pH 7, keeping biomolecules in their optimal ionic state. In multicellular organisms, the pH of extracellular fluids is also tightly regulated. Constancy of pH is achieved primarily by biological buffers: mixtures of weak acids and their conjugate bases.

Buffers Are Mixtures of Weak Acids and Their Conjugate Bases

Buffers are aqueous systems that tend to resist changes in pH when small amounts of acid $mathml alt text526$ $left-parenthesis upper H Superscript plus Baseline right-parenthesis$ or base $mathml alt text527$ $left-parenthesis OH Superscript minus Baseline right-parenthesis$ are added. A buffer system consists of a weak acid (the proton donor) and its conjugate base (the proton acceptor). As an example, a mixture of equal concentrations of acetic acid and acetate ion, found at the midpoint of the titration curve in Figure 2-16, is a buffer system. Notice that the titration curve of acetic acid has a relatively flat zone extending about 1 pH unit on either side of its midpoint pH of 4.76. In this zone, a given amount of $mathml alt text531$ $upper H Superscript plus$ or $mathml alt text532$ $OH Superscript minus$ added to the system has much less effect on pH than the same amount added outside the zone. This relatively flat zone is the buffering region of the acetic acid–acetate buffer pair. At the midpoint of the buffering region, where the concentration of the proton donor (acetic acid) exactly equals that of the proton acceptor (acetate), the buffering power of the system is maximal; that is, its pH changes least on addition of $mathml alt text535$ $upper H Superscript plus$ or $mathml alt text536$ $OH Superscript minus$ . The pH at this point in the titration curve of acetic acid is equal to its apparent $mathml alt text538$ $p upper K Subscript a Baseline$ . The pH of the acetate buffer system does change slightly when a small amount of $mathml alt text540$ $upper H Superscript plus$ or $mathml alt text541$ $OH Superscript minus$ is added, but this change is very small compared with the pH change that would result if the same amount of $mathml alt text543$ $upper H Superscript plus$ or $mathml alt text544$ $OH Superscript minus$ were added to pure water or to a solution of the salt of a strong acid and strong base, such as NaCl, which has no buffering power.

Buffering results from two reversible reaction equilibria occurring in a solution of nearly equal concentrations of a proton donor and its conjugate proton acceptor. Figure 2-18 explains how a buffer system works. Whenever $mathml alt text546$ $upper H Superscript plus$ or $mathml alt text547$ $OH Superscript minus$ is added to a buffer, the result is a small change in the ratio of the relative concentrations of the weak acid and its anion and thus a small change in pH. The decrease in concentration of one component of the system is balanced exactly by an increase in the other. The sum of the buffer components does not change; only their ratio changes.

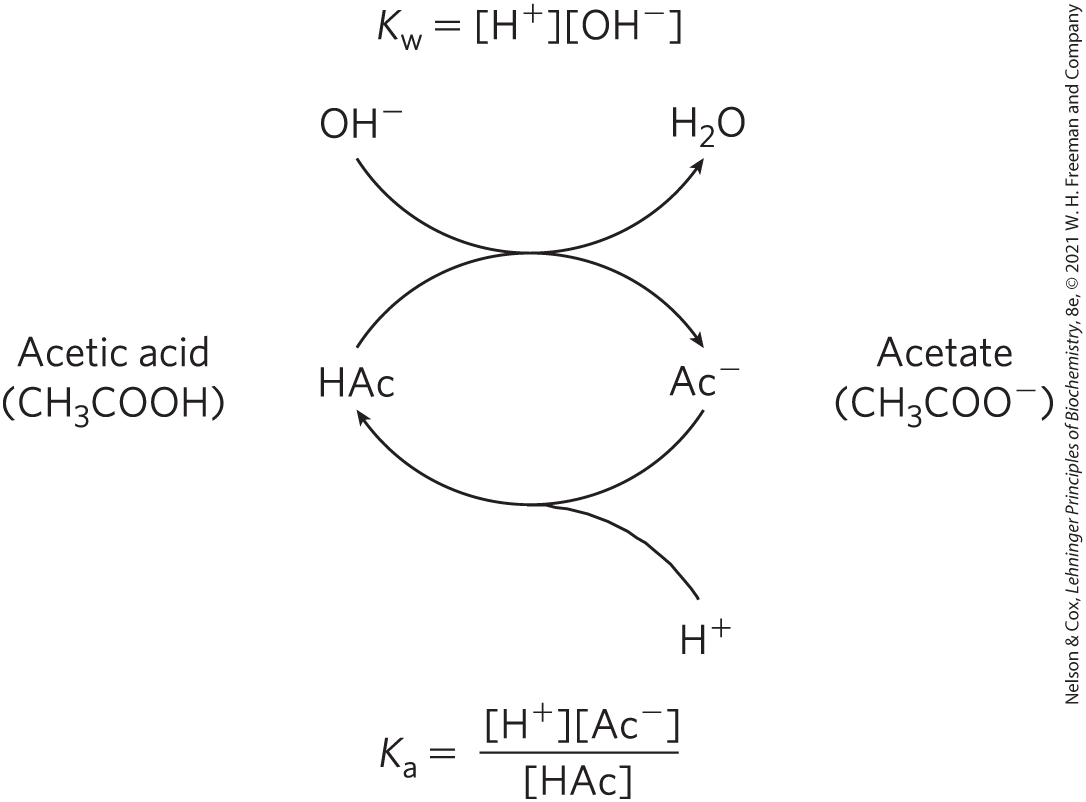
A figure shows how acetic acid and acetate interact as a buffer system. — FIGURE 2-18 The acetic acid–acetate pair as a buffer system. The system is capable of absorbing either $mathml alt text549$ $upper H Superscript plus$ or $mathml alt text550$ $OH Superscript minus$ through the reversibility of the dissociation of acetic acid. The proton donor, acetic acid (HAc), contains a reserve of bound $mathml alt text551$ $upper H Superscript plus$ , which can be released to neutralize an addition of $mathml alt text552$ $OH Superscript minus$ to the system, forming $mathml alt text553$ $upper H Subscript 2 Baseline upper O$ . This happens because the product $mathml alt text554$ $left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket$ transiently exceeds $mathml alt text555$ $upper K Subscript w Baseline left-parenthesis 1 times 10 Superscript minus Superscript 14 Baseline upper M squared right-parenthesis$ . The equilibrium quickly adjusts to restore the product to $mathml alt text556$ $1 times 10 Superscript minus Superscript 14 Baseline upper M Superscript 2$ (at $mathml alt text557$ $25 degree upper C$ ), thus transiently reducing the concentration of $mathml alt text558$ $upper H Superscript plus$ . But now the quotient $mathml alt text559$ $left-bracket upper H Superscript plus Baseline right-bracket left-bracket Ac Superscript minus Baseline right-bracket slash left-bracket HAc right-bracket$ is less than $mathml alt text560$ $upper K Subscript a$ , so HAc dissociates further to restore equilibrium. Similarly, the conjugate base, $mathml alt text561$ $Ac Superscript minus$ , can react with $mathml alt text562$ $upper H Superscript plus$ ions added to the system; again, the two ionization reactions simultaneously come to equilibrium. Thus, a conjugate acid-base pair, such as acetic acid and acetate ion, tends to resist a change in pH when small amounts of acid or base are added. Buffering action is simply the consequence of two reversible reactions taking place simultaneously and reaching their points of equilibrium as governed by their equilibrium constants, $mathml alt text564$ $upper K Subscript w$ and $mathml alt text565$ $upper K Subscript a$ .

FIGURE 2-18 The acetic acid–acetate pair as a buffer system. The system is capable of absorbing either $mathml alt text549$ $upper H Superscript plus$ or $mathml alt text550$ $OH Superscript minus$ through the reversibility of the dissociation of acetic acid. The proton donor, acetic acid (HAc), contains a reserve of bound $mathml alt text551$ $upper H Superscript plus$ , which can be released to neutralize an addition of $mathml alt text552$ $OH Superscript minus$ to the system, forming $mathml alt text553$ $upper H Subscript 2 Baseline upper O$ . This happens because the product $mathml alt text554$ $left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket$ transiently exceeds $mathml alt text555$ $upper K Subscript w Baseline left-parenthesis 1 times 10 Superscript minus Superscript 14 Baseline upper M squared right-parenthesis$ . The equilibrium quickly adjusts to restore the product to $mathml alt text556$ $1 times 10 Superscript minus Superscript 14 Baseline upper M Superscript 2$ (at $mathml alt text557$ $25 degree upper C$ ), thus transiently reducing the concentration of $mathml alt text558$ $upper H Superscript plus$ . But now the quotient $mathml alt text559$ $left-bracket upper H Superscript plus Baseline right-bracket left-bracket Ac Superscript minus Baseline right-bracket slash left-bracket HAc right-bracket$ is less than $mathml alt text560$ $upper K Subscript a$ , so HAc dissociates further to restore equilibrium. Similarly, the conjugate base, $mathml alt text561$ $Ac Superscript minus$ , can react with $mathml alt text562$ $upper H Superscript plus$ ions added to the system; again, the two ionization reactions simultaneously come to equilibrium. Thus, a conjugate acid-base pair, such as acetic acid and acetate ion, tends to resist a change in pH when small amounts of acid or base are added. Buffering action is simply the consequence of two reversible reactions taking place simultaneously and reaching their points of equilibrium as governed by their equilibrium constants, $mathml alt text564$ $upper K Subscript w$ and $mathml alt text565$ $upper K Subscript a$ .

Each conjugate acid-base pair has a characteristic pH zone in which it is an effective buffer (Fig. 2-17). The $mathml alt text567$ $upper H Subscript 2 Baseline PO Subscript 4 Superscript minus Baseline slash HPO Subscript 4 Superscript 2 minus$ pair has a $mathml alt text568$ $p upper K Subscript a Baseline$ of 6.86 and thus can serve as an effective buffer system between approximately pH 5.9 and pH 7.9; the $mathml alt text572$ $NH Subscript 4 Superscript plus Baseline slash NH Subscript 3$ pair, with a $mathml alt text573$ $p upper K Subscript a Baseline$ of 9.25, can act as a buffer between approximately pH 8.3 and pH 10.3.

The Henderson-Hasselbalch Equation Relates $mathml alt text577$ $bold pH$ , $mathml alt text578$ $bold p bold-italic upper K Subscript bold a Baseline$ , and Buffer Concentration

The titration curves of acetic acid, $mathml alt text579$ $upper H Subscript 2 Baseline PO Subscript 4 Superscript 2 minus Baseline comma$ and $mathml alt text580$ $NH Subscript 4 Superscript plus$ (Fig. 2-17) have nearly identical shapes, suggesting that these curves reflect a fundamental law or relationship. This is indeed the case. The shape of the titration curve of any weak acid is described by the Henderson-Hasselbalch equation, which is important for understanding buffer action and acid-base balance in the blood and tissues of vertebrates. This equation is simply a useful way of restating the expression for the ionization constant of an acid. For the ionization of a weak acid HA, the Henderson-Hasselbalch equation can be derived as follows:

K_{a} = \frac{[H^{+}] [A^{-}]}{[HA]}

$upper K Subscript a Baseline equals StartFraction left-bracket upper H Superscript plus Baseline right-bracket left-bracket upper A Superscript minus Baseline right-bracket Over left-bracket HA right-bracket EndFraction$

First solve for [ $mathml alt text583$ $upper H Superscript plus$ ]:

[H^{+}] = K_{a} \frac{[HA]}{[A^{-}]}

$left-bracket upper H Superscript plus Baseline right-bracket equals upper K Subscript a Baseline StartFraction left-bracket HA right-bracket Over left-bracket upper A Superscript minus Baseline right-bracket EndFraction$

Then take the negative logarithm of both sides:

- \log [H^{+}] = - \log K_{a} - \log \frac{[HA]}{[A^{-}]}

$minus log left-bracket upper H Superscript plus Baseline right-bracket equals minus log upper K Subscript a Baseline minus log StartFraction left-bracket HA right-bracket Over left-bracket upper A Superscript minus Baseline right-bracket EndFraction$

Substitute pH for $mathml alt text587$ $minus log left-bracket upper H Superscript plus Baseline right-bracket$ and $mathml alt text588$ $p upper K Subscript a Baseline$ for $mathml alt text589$ $minus log upper K Subscript a Baseline$ :

pH = p K_{a} - \log \frac{[HA]}{[A^{-}]}

$pH equals p upper K Subscript a Baseline minus log StartFraction left-bracket HA right-bracket Over left-bracket upper A Superscript minus Baseline right-bracket EndFraction$

Now invert $mathml alt text591$ $minus log left-bracket HA right-bracket slash left-bracket upper A Superscript minus Baseline right-bracket$ , which requires changing its sign, to obtain the Henderson-Hasselbalch equation:

pH = p K_{a} + \log \frac{[A^{-}]}{[HA]}

$pH equals p upper K Subscript a Baseline plus log StartFraction left-bracket upper A Superscript minus Baseline right-bracket Over left-bracket HA right-bracket EndFraction$

(2-9)

This equation fits the titration curve of all weak acids and enables us to deduce some important quantitative relationships. For example, it shows why the $mathml alt text593$ $p upper K Subscript a Baseline$ of a weak acid is equal to the pH of the solution at the midpoint of its titration. At that point, $mathml alt text595$ $left-bracket HA right-bracket equals left-bracket upper A Superscript minus Baseline right-bracket$ , and

pH = p K_{a} + \log 1 = p K_{a} + 0 = p K_{a}

$pH equals p upper K Subscript a Baseline plus log 1 equals p upper K Subscript a Baseline plus 0 equals p upper K Subscript a Baseline$

The Henderson-Hasselbalch equation also allows us (1) to calculate $mathml alt text597$ $p upper K Subscript a Baseline$ , given pH and the molar ratio of proton donor and acceptor; (2) to calculate pH, given $mathml alt text600$ $p upper K Subscript a Baseline$ and the molar ratio of proton donor and acceptor; and (3) to calculate the molar ratio of proton donor and acceptor, given pH and $mathml alt text602$ $p upper K Subscript a Baseline$ .

Weak Acids or Bases Buffer Cells and Tissues against pH Changes

The intracellular and extracellular fluids of multicellular organisms have a characteristic and nearly constant pH. The organism’s first line of defense against changes in internal pH is provided by buffer systems. The cytoplasm of most cells contains high concentrations of proteins, and these proteins contain many amino acids with functional groups that are weak acids or weak bases. For example, the side chain of histidine (Fig. 2-19) has a $mathml alt text606$ $p upper K Subscript a Baseline$ of 6.0 and thus can exist in either the protonated form or the unprotonated form near neutral pH. Proteins containing histidine residues therefore buffer effectively near neutral pH.

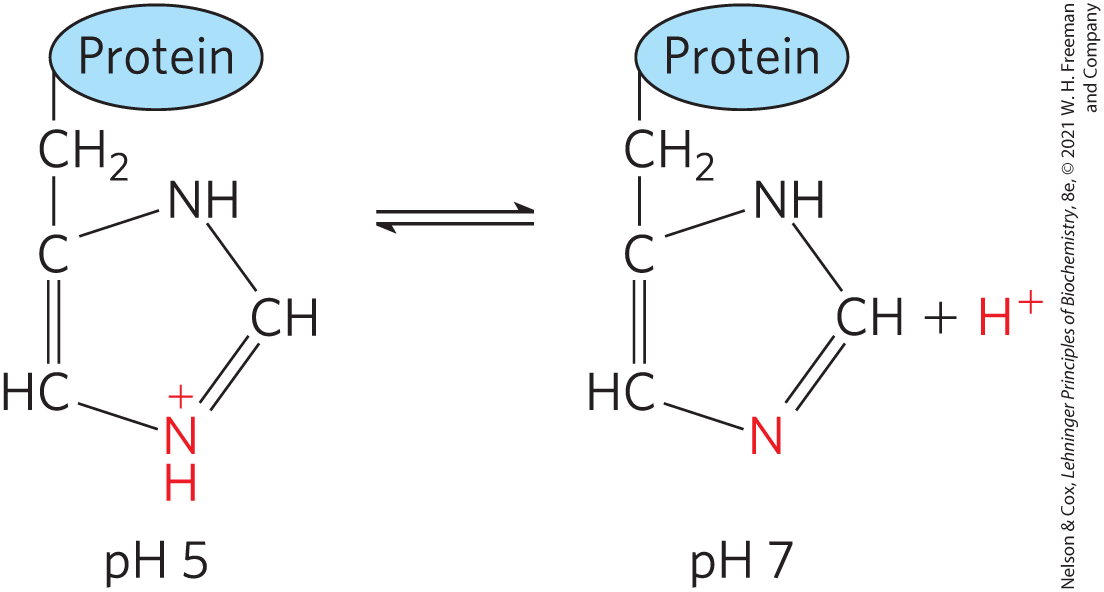
A figure shows the ionization of histidine during a transition from p H 5 to p H 7. — FIGURE 2-19 Ionization of histidine. The amino acid histidine, a component of proteins, is a weak acid. The $mathml alt text610$ $p upper K Subscript a Baseline$ of the protonated nitrogen of the side chain is 6.0.

WORKED EXAMPLE 2-4 Ionization of Histidine

Calculate the fraction of histidine that has its imidazole side chain protonated at pH 7.3. The $mathml alt text612$ $p upper K Subscript a Baseline$ values for histidine are $mathml alt text613$ $p upper K 1 equals 1.8$ , $mathml alt text614$ $p upper K 2 left-parenthesis imidazole right-parenthesis equals 6.0$ , and $mathml alt text615$ $p upper K 3 equals 9.2$ (see Fig. 3-12b).

SOLUTION:

The three ionizable groups in histidine have sufficiently different $mathml alt text616$ $p upper K Subscript a Baseline$ values (different by at least 2 pH units) that the first acid $mathml alt text618$ $left-parenthesis em-dash COOH right-parenthesis$ is almost completely ionized before the second acid (protonated imidazole) begins to dissociate a proton, and the second ionizes almost completely before the third $mathml alt text619$ $left-parenthesis em-dash NH Subscript 3 Superscript plus Baseline right-parenthesis$ begins to dissociate its proton. (With the Henderson-Hasselbalch equation, we can easily show that a weak acid goes from 1% ionized at 2 pH units below its $mathml alt text622$ $p upper K Subscript a Baseline$ to 99% ionized at 2 pH units above its $mathml alt text625$ $p upper K Subscript a Baseline$ ; see also Fig. 3-12b.) At pH 7.3, the carboxyl group of histidine is entirely deprotonated $mathml alt text627$ $left-parenthesis em-dash COO Superscript minus Baseline right-parenthesis$ and the α-amino group is fully protonated $mathml alt text628$ $left-parenthesis em-dash NH Subscript 3 Superscript plus Baseline right-parenthesis$ . We can therefore assume that at pH 7.3, the only group that is partially dissociated is the imidazole group, which can be protonated (we’ll abbreviate as $mathml alt text630$ $His upper H Superscript plus$ ) or not (His).

We use the Henderson-Hasselbalch equation:

pH = p K_{a} + \log \frac{[A^{-}]}{[HA]}

$pH equals p upper K Subscript a Baseline plus log StartFraction left-bracket upper A Superscript minus Baseline right-bracket Over left-bracket HA right-bracket EndFraction$

Substituting $mathml alt text633$ $p upper K 2 equals 6.0$ and pH = 7.3:

\begin{matrix} 7.3 & = 6.0 + \log \frac{[His]}{[{HisH}^{+}]} \\ 1.3 & = + \log \frac{[His]}{[{HisH}^{+}]} \\ antilog 1 .3 & = \frac{[His]}{[{HisH}^{+}]} = 2.0 \times 10^{1} \end{matrix}

$StartLayout 1st Row 1st Column 7.3 2nd Column equals 6.0 plus log StartFraction left-bracket His right-bracket Over left-bracket HisH Superscript plus Baseline right-bracket EndFraction 2nd Row 1st Column 1.3 2nd Column equals plus log StartFraction left-bracket His right-bracket Over left-bracket HisH Superscript plus Baseline right-bracket EndFraction 3rd Row 1st Column antilog 1 .3 2nd Column equals StartFraction left-bracket His right-bracket Over left-bracket HisH Superscript plus Baseline right-bracket EndFraction equals 2.0 times 10 Superscript 1 EndLayout$

This gives us the ratio of [His] to $mathml alt text637$ $left-bracket His upper H Superscript plus Baseline right-bracket$ (20 to 1 in this case). We want to convert this ratio to the fraction of total histidine that is in the unprotonated form (His) at pH 7.3. That fraction is 20/21 (20 parts His per 1 part $mathml alt text639$ $His upper H Superscript plus$ , in a total of 21 parts histidine in either form), or about 95.2%; the remainder (100% minus 95.2%) is protonated—about 5%.

Nucleotides such as ATP, as well as many metabolites of low molecular weight, contain ionizable groups that can contribute buffering power to the cytoplasm. Some highly specialized organelles and extracellular compartments have high concentrations of compounds that contribute buffering capacity: organic acids buffer the vacuoles of plant cells; ammonia buffers urine.

Two especially important biological buffers are the phosphate and bicarbonate systems. The phosphate buffer system, which acts in the cytoplasm of all cells, consists of $mathml alt text644$ $upper H Subscript 2 Baseline PO Subscript 4 Superscript minus$ as proton donor and $mathml alt text645$ $HPO Subscript 4 Superscript 2 minus$ as proton acceptor:

H_{2} {PO}_{4}^{-} ⇌ H^{+} + {HPO}_{4}^{2 -}

$upper H Subscript 2 Baseline PO Subscript 4 Superscript minus Baseline right harpoon over left harpoon upper H Superscript plus Baseline plus HPO Subscript 4 Superscript 2 minus$

The phosphate buffer system is maximally effective at a pH close to its $mathml alt text648$ $p upper K Subscript a Baseline$ of 6.86 (Figs 2-15, 2-17) and thus tends to resist pH changes in the range between about 5.9 and 7.9. It is therefore an effective buffer in biological fluids; in mammals, for example, extracellular fluids and most cytoplasmic compartments have a pH in the range of 6.9 to 7.4.

WORKED EXAMPLE 2-5 Phosphate Buffers

(a) What is the pH of a mixture of $mathml alt text657$ $0.042 upper M NaH Subscript 2 Baseline PO Subscript 4 Baseline$ and $mathml alt text658$ $0.058 upper M Na Subscript 2 Baseline HPO Subscript 4 Baseline$ ?

SOLUTION:

We use the Henderson-Hasselbalch equation, which we’ll express here as

pH = p K_{a} + \log \frac{[conjugate base]}{[acid]}

$pH equals p upper K Subscript a Baseline plus log StartFraction left-bracket conjugate base right-bracket Over left-bracket acid right-bracket EndFraction$

In this case, the acid (the species that gives up a proton) is $mathml alt text660$ $upper H Subscript 2 Baseline PO Subscript 4 Superscript minus$ , and the conjugate base (the species that gains a proton) is $mathml alt text661$ $HPO Subscript 4 Superscript 2 minus$ . Substituting the given concentrations of acid and conjugate base and the $mathml alt text662$ $p upper K Subscript a Baseline left-parenthesis 6.86 right-parenthesis$ results in

pH = 6 .86 + \log \frac{[0.058]}{[0.042]} = 6.86 + 0.14 = 7.0

$pH equals 6 .86 plus log StartFraction left-bracket 0.058 right-bracket Over left-bracket 0.042 right-bracket EndFraction equals 6.86 plus 0.14 equals 7.0$

We can roughly check this answer. When more conjugate base than acid is present, the acid is more than 50% titrated and thus the pH is above the $mathml alt text666$ $p upper K Subscript a Baseline left-parenthesis 6.86 right-parenthesis$ , where the acid is exactly 50% titrated.

(b) If 1.0 mL of 10.0 m NaOH is added to a liter of the buffer prepared in (a), how much will the pH change?

SOLUTION:

A liter of the buffer contains 0.042 mol of $mathml alt text672$ $NaH Subscript 2 Baseline PO Subscript 4$ . Adding 1.0 mL of 10.0 m NaOH (0.010 mol) would titrate an equivalent amount (0.010 mol) of $mathml alt text676$ $NaH Subscript 2 Baseline PO Subscript 4$ to $mathml alt text677$ $Na Subscript 2 Baseline HPO Subscript 4$ , resulting in 0.032 mol of $mathml alt text679$ $NaH Subscript 2 Baseline PO Subscript 4$ and 0.068 mol of $mathml alt text681$ $Na Subscript 2 Baseline HPO Subscript 4$ . The new pH is

\begin{matrix} pH & = p K_{a} + \log \frac{[{HPO}_{4}^{2 -}]}{[H_{2} {PO}_{4}^{-}]} \\ = 6.86 + \log \frac{0.068}{0.032} = 6.86 + 0.33 = 7.2 \end{matrix}

$StartLayout 1st Row 1st Column pH 2nd Column equals p upper K Subscript a Baseline plus log StartFraction left-bracket HPO Subscript 4 Superscript 2 minus Baseline right-bracket Over left-bracket upper H Subscript 2 Baseline PO Subscript 4 Superscript minus Baseline right-bracket EndFraction 2nd Row 1st Column Blank 2nd Column equals 6.86 plus log StartFraction 0.068 Over 0.032 EndFraction equals 6.86 plus 0.33 equals 7.2 EndLayout$

(c) If 1.0 mL of 10.0 m NaOH is added to a liter of pure water at pH 7.0, what is the final pH? Compare this with the answer in (b).

SOLUTION:

The NaOH dissociates completely into $mathml alt text689$ $Na Superscript plus$ and $mathml alt text690$ $OH Superscript minus$ , giving $mathml alt text691$ $left-bracket OH Superscript minus Baseline right-bracket equals 0.010 mol slash upper L equals 1.0 times 10 Superscript minus squared upper M$ . We can define a term pOH analogous with pH to express $mathml alt text694$ $left-bracket OH Superscript minus Baseline right-bracket$ of a solution. The pOH is the negative logarithm of $mathml alt text696$ $left-bracket OH Superscript minus Baseline right-bracket$ , so in our example pOH = 2.0. Given that in all solutions, pH + pOH = 14 (see Table 2-5), the pH of the solution is 12. So, an amount of NaOH that increases the pH of water from 7 to 12 increases the pH of a buffered solution, as in (b), from 7.0 to just 7.2. Such is the power of buffering!

Why is pH + pOH = 14?

K_{w} = 10^{- 14} = [H^{+}] [{OH}^{-}]

$upper K Subscript w Baseline equals 10 Superscript negative 14 Baseline equals left-bracket upper H Superscript plus Baseline right-bracket left-bracket OH Superscript minus Baseline right-bracket$

Taking the negative log of both sides of the equation gives

\begin{matrix} - log (10^{- 14}) = - log [H^{+}] + - log [{OH}^{-}] \\ 14 = - log [H^{+}] + - log [{OH}^{-}] \\ 14 = pH + pOH \end{matrix}

$StartLayout 1st Row minus log left-parenthesis 10 Superscript negative 14 Baseline right-parenthesis equals minus log left-bracket upper H Superscript plus Baseline right-bracket plus minus log left-bracket OH Superscript minus Baseline right-bracket 2nd Row 14 equals minus log left-bracket upper H Superscript plus Baseline right-bracket plus minus log left-bracket OH Superscript minus Baseline right-bracket 3rd Row 14 equals pH plus pOH EndLayout$

Blood plasma is buffered in part by the bicarbonate system, consisting of carbonic acid $mathml alt text706$ $left-parenthesis upper H Subscript 2 Baseline CO Subscript 3 Baseline right-parenthesis$ as proton donor and bicarbonate $mathml alt text707$ $left-parenthesis HCO Subscript 3 Superscript minus Baseline right-parenthesis$ as proton acceptor ( $mathml alt text708$ $upper K 1$ is the first of several equilibrium constants in the bicarbonate buffering system):

\begin{matrix} H_{2} {CO}_{3} ⇌ H^{+} + {HCO}_{3}^{-} \\ K_{1} = \frac{[H^{+}] [{HCO}_{3}^{-}]}{[H_{2} {CO}_{3}^{}]} \end{matrix}

$StartLayout 1st Row upper H Subscript 2 Baseline CO Subscript 3 Baseline right harpoon over left harpoon upper H Superscript plus Baseline plus HCO Subscript 3 Superscript minus Baseline 2nd Row upper K 1 equals StartFraction left-bracket upper H Superscript plus Baseline right-bracket left-bracket HCO Subscript 3 Superscript minus Baseline right-bracket Over left-bracket upper H Subscript 2 Baseline CO Subscript 3 Superscript Baseline right-bracket EndFraction EndLayout$

This buffer system is more complex than other conjugate acid-base pairs because one of its components, carbonic acid $mathml alt text711$ $left-parenthesis upper H Subscript 2 Baseline CO Subscript 3 Baseline right-parenthesis$ , is formed from dissolved (aq) carbon dioxide and water, in a reversible reaction:

\begin{matrix} {CO}_{2} (aq) + H_{2} O ⇌ H_{2} {CO}_{3} \\ K_{2} = \frac{[H_{2} {CO}_{3}^{}]}{[{CO}_{2}^{} (aq)] [H_{2} O]} \end{matrix}

$StartLayout 1st Row CO Subscript 2 Baseline left-parenthesis aq right-parenthesis plus upper H Subscript 2 Baseline upper O right harpoon over left harpoon upper H Subscript 2 Baseline CO Subscript 3 Baseline 2nd Row upper K 2 equals StartFraction left-bracket upper H Subscript 2 Baseline CO Subscript 3 Superscript Baseline right-bracket Over left-bracket CO Subscript 2 Superscript Baseline left-parenthesis aq right-parenthesis right-bracket left-bracket upper H Subscript 2 Baseline upper O right-bracket EndFraction EndLayout$

Carbon dioxide is a gas under normal conditions, and $mathml alt text714$ $CO Subscript 2$ dissolved in an aqueous solution is in equilibrium with $mathml alt text715$ $CO Subscript 2$ in the gas (g) phase:

\begin{matrix} {CO}_{2} (g) ⇌ {CO}_{2}^{} (aq) \\ K_{a} = \frac{[{CO}_{2}^{} (aq)]}{[{CO}_{2}^{} (g)]} \end{matrix}

$StartLayout 1st Row CO Subscript 2 Baseline left-parenthesis g right-parenthesis right harpoon over left harpoon CO Subscript 2 Superscript Baseline left-parenthesis aq right-parenthesis 2nd Row upper K Subscript a Baseline equals StartFraction left-bracket CO Subscript 2 Superscript Baseline left-parenthesis aq right-parenthesis right-bracket Over left-bracket CO Subscript 2 Superscript Baseline left-parenthesis g right-parenthesis right-bracket EndFraction EndLayout$

The pH of a bicarbonate buffer system depends on the concentrations of $mathml alt text719$ $upper H Subscript 2 Baseline CO Subscript 3$ and $mathml alt text720$ $HCO Subscript 3 Superscript minus$ , the proton donor and acceptor components. The concentration of $mathml alt text721$ $upper H Subscript 2 Baseline CO Subscript 3$ in turn depends on the concentration of dissolved $mathml alt text722$ $CO Subscript 2$ , which in turn depends on the concentration of $mathml alt text723$ $CO Subscript 2$ in the gas phase, or the partial pressure of $mathml alt text724$ $CO Subscript 2$ , denoted $mathml alt text725$ $pCO Subscript 2$ . Thus, the pH of a bicarbonate buffer exposed to a gas phase is ultimately determined by the concentration of $mathml alt text727$ $HCO Subscript 3 Superscript minus$ in the aqueous phase and by $mathml alt text728$ $pCO Subscript 2$ in the gas phase.

The bicarbonate buffer system is an effective physiological buffer near pH 7.4, because the $mathml alt text730$ $upper H Subscript 2 Baseline CO Subscript 3$ of blood plasma is in equilibrium with a large reserve capacity of $mathml alt text731$ $CO Subscript 2 Baseline left-parenthesis g right-parenthesis$ in the air space of the lungs. As noted above, this buffer system involves three reversible equilibria, in this case between gaseous $mathml alt text732$ $CO Subscript 2$ in the lungs and bicarbonate $mathml alt text733$ $left-parenthesis HCO Subscript 3 Superscript minus Baseline right-parenthesis$ in the blood plasma (Fig. 2-20).

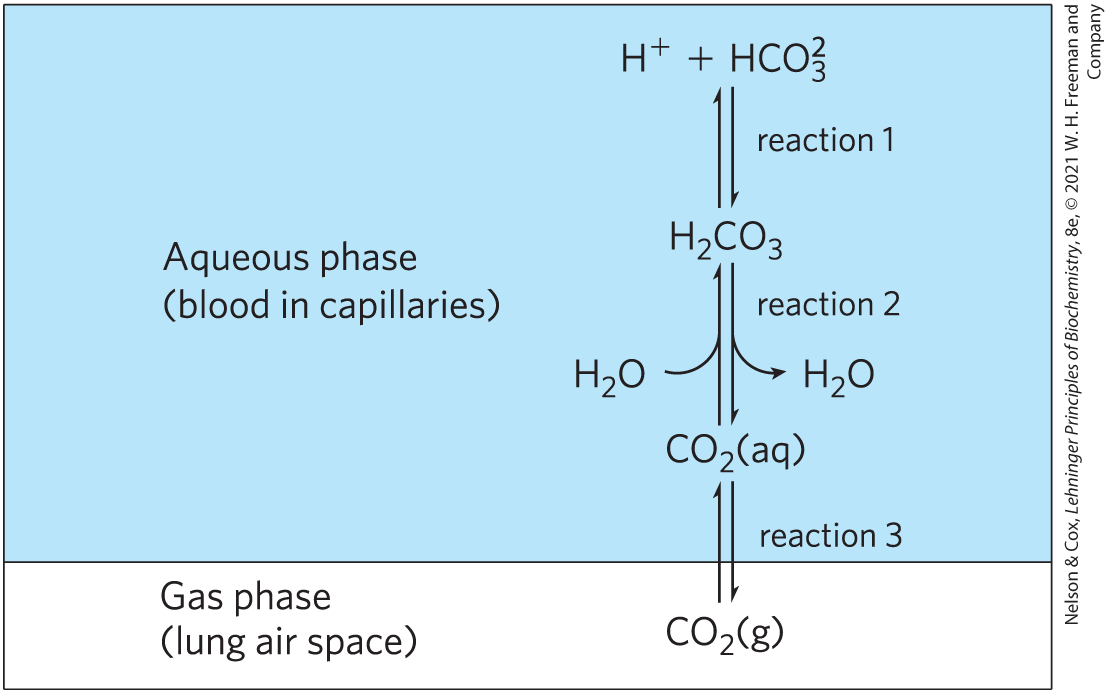
A figure shows the reactions of the bicarbonate buffer system in blood in capillaries and air in lungs. — FIGURE 2-20 The bicarbonate buffer system. $mathml alt text734$ $CO Subscript 2$ in the air space of the lungs is in equilibrium with the bicarbonate buffer in the blood plasma passing through the lung capillaries. Because the concentration of dissolved $mathml alt text735$ $CO Subscript 2$ can be adjusted rapidly through changes in the rate of breathing, the bicarbonate buffer system of the blood is in near-equilibrium with a large potential reservoir of $mathml alt text736$ $CO Subscript 2$ .

FIGURE 2-20 The bicarbonate buffer system. $mathml alt text734$ $CO Subscript 2$ in the air space of the lungs is in equilibrium with the bicarbonate buffer in the blood plasma passing through the lung capillaries. Because the concentration of dissolved $mathml alt text735$ $CO Subscript 2$ can be adjusted rapidly through changes in the rate of breathing, the bicarbonate buffer system of the blood is in near-equilibrium with a large potential reservoir of $mathml alt text736$ $CO Subscript 2$ .

Blood can pick up $mathml alt text737$ $upper H Superscript plus$ , such as from the lactic acid produced in muscle tissue during vigorous exercise. Alternatively, it can lose $mathml alt text738$ $upper H Superscript plus$ , such as by protonation of the $mathml alt text739$ $NH Subscript 3$ produced during protein catabolism. When $mathml alt text740$ $upper H Superscript plus$ is added to blood as it passes through the tissues, reaction 1 in Figure 2-20 proceeds toward a new equilibrium, in which [ $mathml alt text741$ $upper H Subscript 2 Baseline CO Subscript 3$ ] is increased. This in turn increases [ $mathml alt text742$ $CO Subscript 2 Baseline left-parenthesis aq right-parenthesis$ ] in the blood (reaction 2) and thus increases the partial pressure of $mathml alt text743$ $CO Subscript 2 Baseline left-parenthesis g right-parenthesis$ in the air space of the lungs (reaction 3); the extra $mathml alt text744$ $CO Subscript 2$ is exhaled. Conversely, when $mathml alt text745$ $upper H Superscript plus$ is lost from the blood, the opposite events occur: more $mathml alt text746$ $upper H Subscript 2 Baseline CO Subscript 3$ dissociates into $mathml alt text747$ $upper H Superscript plus$ and $mathml alt text748$ $HCO Subscript 3 Superscript minus$ , and thus more $mathml alt text749$ $CO Subscript 2 Baseline left-parenthesis g right-parenthesis$ from the lungs dissolves in blood plasma. The rate of respiration—that is, the rate of inhaling and exhaling—can quickly adjust these equilibria to keep the blood pH nearly constant. The rate of respiration is controlled by the brain stem, where detection of an increased blood $mathml alt text751$ $pCO Subscript 2$ or decreased blood pH triggers deeper and more frequent breathing.

Hyperventilation, the rapid breathing sometimes elicited by stress or anxiety, tips the normal balance of $mathml alt text753$ $upper O Subscript 2$ breathed in and $mathml alt text754$ $CO Subscript 2$ breathed out in favor of too much $mathml alt text755$ $CO Subscript 2$ breathed out, raising the blood pH to 7.45 or higher and causing alkalosis. This alkalosis can lead to dizziness, headache, weakness, and fainting. One home remedy for mild alkalosis is to breathe briefly into a paper bag. The air in the bag becomes enriched in $mathml alt text758$ $CO Subscript 2$ , and inhaling this air increases the $mathml alt text759$ $CO Subscript 2$ concentration in the body and blood and decreases blood pH.

At the normal pH of blood plasma (7.4), very little $mathml alt text763$ $upper H Subscript 2 Baseline CO Subscript 3$ is present relative to $mathml alt text764$ $HCO Subscript 3 Superscript minus Baseline comma$ and the addition of just a small amount of base ( $mathml alt text765$ $NH Subscript 3$ or $mathml alt text766$ $OH Superscript minus$ ) would titrate this $mathml alt text767$ $upper H Subscript 2 Baseline CO Subscript 3$ , exhausting the buffering capacity. The important role of $mathml alt text768$ $upper H Subscript 2 Baseline CO Subscript 3 Baseline left-parenthesis p upper K Subscript a Baseline equals 3.57$ at $mathml alt text769$ $37 degree upper C$ ) in buffering blood plasma (pH ∼ 7.4) seems inconsistent with our earlier statement that a buffer is most effective in the range of 1 pH unit above and below its $mathml alt text772$ $p upper K Subscript a Baseline$ . The explanation for this apparent paradox is the large reservoir of $mathml alt text773$ $CO Subscript 2$ dissolved in blood, which we refer to as $mathml alt text774$ $CO Subscript 2 Baseline left-parenthesis aq right-parenthesis$ . Its rapid equilibration with $mathml alt text775$ $upper H Subscript 2 Baseline CO Subscript 3$ results in the formation of additional $mathml alt text776$ $upper H Subscript 2 Baseline CO Subscript 3$ :

{CO}_{2} (aq) + H_{2} O ⇌ H_{2} {CO}_{3}^{}

$CO Subscript 2 Baseline left-parenthesis aq right-parenthesis plus upper H Subscript 2 Baseline upper O right harpoon over left harpoon upper H Subscript 2 Baseline CO Subscript 3 Superscript$

It is useful in clinical medicine to have a simple expression for blood pH in terms of $mathml alt text779$ $CO Subscript 2 Baseline left-parenthesis aq right-parenthesis$ , which is commonly monitored along with other blood gases. We can define a constant, $mathml alt text780$ $upper K Subscript h$ , which is the equilibrium constant for the hydration of $mathml alt text781$ $CO Subscript 2$ to form $mathml alt text782$ $upper H Subscript 2 Baseline CO Subscript 3$ :

K_{h} = \frac{[H_{2} {CO}_{3}^{}]}{[{CO}_{2}^{} (aq)]}

$upper K Subscript h Baseline equals StartFraction left-bracket upper H Subscript 2 Baseline CO Subscript 3 Superscript Baseline right-bracket Over left-bracket CO Subscript 2 Superscript Baseline left-parenthesis aq right-parenthesis right-bracket EndFraction$

(The concentration of water is so high (55.5 m) that dissolving $mathml alt text785$ $CO Subscript 2$ doesn’t change $mathml alt text786$ $left-bracket upper H Subscript 2 Baseline upper O right-bracket$ appreciably, so $mathml alt text787$ $left-bracket upper H Subscript 2 Baseline upper O right-bracket$ is made part of the constant $mathml alt text788$ $upper K Subscript h$ .) Then, to take the $mathml alt text789$ $CO Subscript 2 Baseline left-parenthesis aq right-parenthesis$ reservoir into account, we can express $mathml alt text790$ $left-bracket upper H Subscript 2 Baseline CO Subscript 3 Baseline right-bracket$ as $mathml alt text791$ $upper K Subscript h Baseline left-bracket CO Subscript 2 Baseline left-parenthesis aq right-parenthesis right-bracket$ and substitute this expression for $mathml alt text792$ $left-bracket upper H Subscript 2 Baseline CO Subscript 3 Baseline right-bracket$ in the equation for the acid dissociation of $mathml alt text793$ $upper H Subscript 2 Baseline CO Subscript 3$ :

K_{a} = \frac{[H^{+}] [{HCO}_{3}^{-}]}{[H_{2} {CO}_{3}]} = \frac{[H^{+}] [{HCO}_{3}^{-}]}{K_{h} [{CO}_{2} (aq)]}

$upper K Subscript a Baseline equals StartFraction left-bracket upper H Superscript plus Baseline right-bracket left-bracket HCO Subscript 3 Superscript minus Baseline right-bracket Over left-bracket upper H Subscript 2 Baseline CO Subscript 3 Baseline right-bracket EndFraction equals StartFraction left-bracket upper H Superscript plus Baseline right-bracket left-bracket HCO Subscript 3 Superscript minus Baseline right-bracket Over upper K Subscript h Baseline left-bracket CO Subscript 2 Baseline left-parenthesis aq right-parenthesis right-bracket EndFraction$

Now, the overall equilibrium for dissociation of $mathml alt text795$ $upper H Subscript 2 Baseline CO Subscript 3$ can be expressed in these terms:

K_{h} K_{a} = K_{combined} = \frac{[H^{+}] [{HCO}_{3}^{-}]}{[{CO}_{2} (aq)]}

$upper K Subscript h Baseline upper K Subscript a Baseline equals upper K Subscript combined Baseline equals StartFraction left-bracket upper H Superscript plus Baseline right-bracket left-bracket HCO Subscript 3 Superscript minus Baseline right-bracket Over left-bracket CO Subscript 2 Baseline left-parenthesis aq right-parenthesis right-bracket EndFraction$

We can calculate the value of the new constant, $mathml alt text797$ $upper K Subscript combined$ , and the corresponding apparent pK, or $mathml alt text799$ $p upper K Subscript combined Baseline$ , from the experimentally determined values of $mathml alt text800$ $upper K Subscript h Baseline left-parenthesis 3.0 times 10 Superscript negative 3 Baseline upper M right-parenthesis$ and $mathml alt text801$ $upper K Subscript a Baseline left-parenthesis 2.7 times 10 Superscript negative 4 Baseline upper M right-parenthesis$ at $mathml alt text802$ $37 Superscript degree Baseline upper C$ :

\begin{array}{l} K_{combined} & = (3.0 \times 10^{- 3} M) (2.7 \times 10^{- 4} M) \\ = 8.1 \times 10^{- 7} M^{2} \\ p K_{combined} & = 6.1 \end{array}

$StartLayout 1st Row 1st Column upper K Subscript combined 2nd Column equals left-parenthesis 3.0 times 10 Superscript negative 3 Baseline upper M right-parenthesis left-parenthesis 2.7 times 10 Superscript negative 4 Baseline upper M right-parenthesis 2nd Row 1st Column Blank 2nd Column equals 8.1 times 10 Superscript negative 7 Baseline upper M squared 3rd Row 1st Column p upper K Subscript combined Baseline 2nd Column equals 6.1 EndLayout$

In clinical medicine, it is common to refer to $mathml alt text804$ $CO Subscript 2 Baseline left-parenthesis aq right-parenthesis$ as the conjugate acid and to use the apparent, or combined, $mathml alt text805$ $p upper K Subscript a Baseline$ of 6.1 to simplify calculation of pH from $mathml alt text808$ $left-bracket CO Subscript 2 Baseline left-parenthesis aq right-parenthesis right-bracket$ . The concentration of dissolved $mathml alt text809$ $CO Subscript 2$ is a function of $mathml alt text810$ $pCO Subscript 2$ , which in the lung is about 4.8 kilopascals (kPa), corresponding to $mathml alt text812$ $left-bracket upper H Subscript 2 Baseline CO Subscript 3 Baseline right-bracket almost-equals 1.2 mM$ . Plasma $mathml alt text813$ $left-bracket HCO Subscript 3 Superscript minus Baseline right-bracket$ is normally about 24 mm, so $mathml alt text815$ $left-bracket HCO Subscript 3 Superscript minus Baseline right-bracket slash left-bracket upper H Subscript 2 Baseline CO Subscript 3 Baseline right-bracket$ is about 20, and the blood pH is 6.1 + log 20 ≈ 7.4.

Untreated Diabetes Produces Life-Threatening Acidosis

Many of the enzymes that function in the blood have evolved to have maximal activity between pH 7.35 and 7.45, the normal pH range of human blood plasma. Enzymes typically show maximal catalytic activity at a characteristic pH, called the optimum pH (Fig. 2-21). On either side of this optimum pH, catalytic activity often declines sharply. Thus, a small change in pH can make a large difference in the rate of some crucial enzyme-catalyzed reactions. Biological control of the pH of cells and body fluids is therefore of central importance in all aspects of metabolism and cellular activities, and changes in blood pH have marked physiological consequences, as we know from the alarming experiments described in Box 2-1.

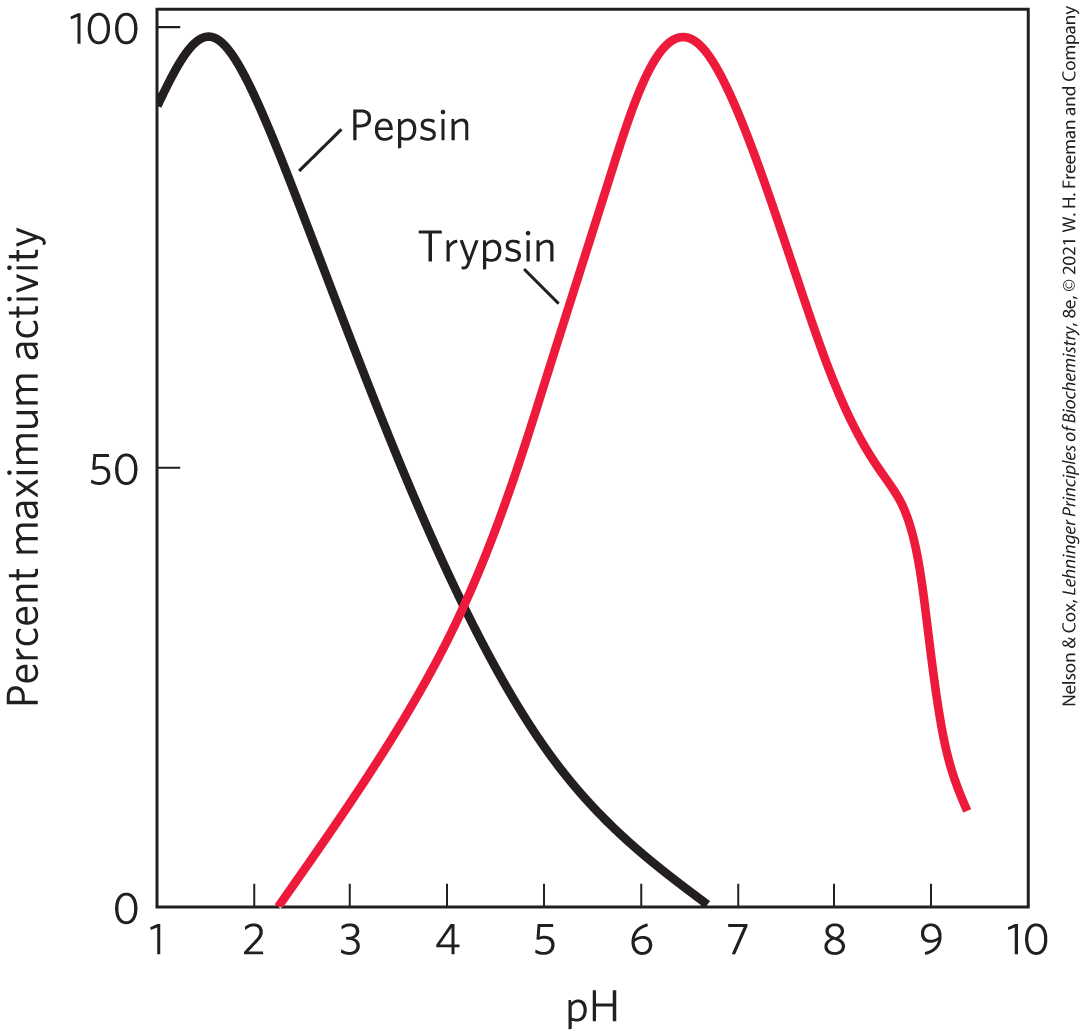
A graph plotting percent maximum activity against p H compares the p H optima of pepsin and trypsin. — FIGURE 2-21 The pH optima of two enzymes. Pepsin is a digestive enzyme secreted into gastric juice, which has a pH of ∼1.5, allowing pepsin to act optimally. Trypsin, a digestive enzyme that acts in the small intestine, has a pH optimum that matches the neutral pH in the lumen of the small intestine.

In individuals with untreated diabetes mellitus, the lack of insulin, or insensitivity to insulin, disrupts the uptake of glucose from blood into the tissues and forces the tissues to use stored fatty acids as their primary fuel. For reasons we describe in detail later in the book (see Chapter 23), this dependence on fatty acids results in acidosis, the accumulation of high concentrations of two carboxylic acids, β-hydroxybutyric acid and acetoacetic acid (a combined blood plasma level of 90 mg/100 mL, compared with <3 mg/100 mL in control (healthy) individuals; urinary excretion of 5 g/24 h, compared with <125 mg/24 h in controls). Dissociation of these acids lowers the pH of blood plasma to less than 7.35. Severe acidosis (characterized by low blood pH) produces headache, drowsiness, nausea, vomiting, and diarrhea, followed by stupor, coma, and convulsions, presumably because, at the lower pH, some enzyme(s) do not function optimally. When a patient is found to have high blood glucose, low plasma pH, and high levels of β-hydroxybutyric acid and acetoacetic acid in blood and urine, diabetes mellitus is the likely diagnosis.

Other conditions can also produce acidosis. For example, fasting and starvation force the use of stored fatty acids as fuel, with the same consequences as for diabetes. Very heavy exertion, such as a sprint by runners or cyclists, leads to temporary accumulation of lactic acid in the blood. Kidney failure results in a diminished capacity to regulate bicarbonate levels. Lung diseases (such as emphysema, pneumonia, and asthma) reduce the capacity to dispose of the $mathml alt text842$ $CO Subscript 2$ produced by fuel oxidation in the tissues, with the resulting accumulation of $mathml alt text843$ $upper H Subscript 2 Baseline CO Subscript 3$ .

Acidosis is treated by dealing with the underlying condition—administering insulin to people with diabetes, and steroids or antibiotics to people with lung disease. Severe acidosis can be reversed by administering bicarbonate solution intravenously.

WORKED EXAMPLE 2-6 Treatment of Acidosis with Bicarbonate

Why does intravenous administration of a bicarbonate solution raise the plasma pH?

SOLUTION:

The ratio of $mathml alt text845$ $left-bracket HCO Subscript 3 Superscript minus Baseline right-bracket$ to $mathml alt text846$ $left-bracket CO Subscript 2 Baseline left-parenthesis aq right-parenthesis right-bracket$ determines the pH of the bicarbonate buffer, according to the equation

pH = 6.1 + \log \frac{[{HCO}_{3}^{-}]}{H_{2} {CO}_{3}^{}}

$pH equals 6.1 plus log StartFraction left-bracket HCO Subscript 3 Superscript minus Baseline right-bracket Over upper H Subscript 2 Baseline CO Subscript 3 Superscript Baseline EndFraction$

where $mathml alt text849$ $left-bracket upper H Subscript 2 Baseline CO Subscript 3 Baseline right-bracket$ is directly related to $mathml alt text850$ $pCO Subscript 2$ , the partial pressure of $mathml alt text851$ $CO Subscript 2$ . So, if $mathml alt text852$ $left-bracket HCO Subscript 3 Superscript minus Baseline right-bracket$ is increased with no change in $mathml alt text853$ $pCO Subscript 2$ , the blood pH will rise.

SUMMARY 2.3 Buffering against pH Changes in Biological Systems

A mixture of a weak acid (or base) and its salt resists changes in pH caused by the addition of $mathml alt text857$ $upper H Superscript plus$ or $mathml alt text858$ $OH Superscript minus$ . The mixture thus functions as a buffer.
The pH of a solution of a weak acid (or base) and its salt is given by the Henderson-Hasselbalch equation:
$pH = p K_{a} + \log \frac{[A^{-}]}{[HA]}$ $pH equals p upper K Subscript a Baseline plus log StartFraction left-bracket upper A Superscript minus Baseline right-bracket Over left-bracket HA right-bracket EndFraction$
In cells and tissues, phosphate and bicarbonate buffer systems maintain intracellular and extracellular fluids near pH 7.4. Enzymes generally work optimally near this physiological pH.
Medical conditions such as untreated diabetes that lower the pH of blood, causing acidosis, or raise it, causing alkalosis, can be life-threatening.