Modeling Logistical Growth

• http://pindling.org/Math/Precalc/Current/Textbook/Functions/rates_ratios.html

• https://www.khanacademy.org/math/algebra2/x2ec2f6f830c9fb89:exp-model/x2ec2f6f830c9fb89:exp-change/v/interpreting-change-in-exponential-models

• https://www.uwyo.edu/dbmcd/popecol/janlects/lect05.html

Exponential Growth

• To understand the rate of change of the population over time , we differentiate $P$$P$ with respect to $t$$t$ :

• this is fine as is , but since we already know $P$$P$ , we can simplify to :

• The explicit version $(P=P_0\ast e^{r\ast t})$$\left(\ P = P_0 * e^{r*t} \ \right)$ gives the population size at any time $\left(t\right)$$\left(\ t \ \right)$ , assuming exponential growth.

• The differential version $(\frac{dP}{dt}=r\ast P)$$\left(\ \frac{dP}{dt} = r * P \ \right)$ , describes how the population's rate of change at any moment is proportional to the current population size.

  • "the change in population size over an infinitesimally small time interval is directly proportional to the size of the population at that moment"

• The explicit version gives a specific solution given some initial conditions

• The differential version provides enables modeling at any moment in time , and is not tied to a specific initial condition.

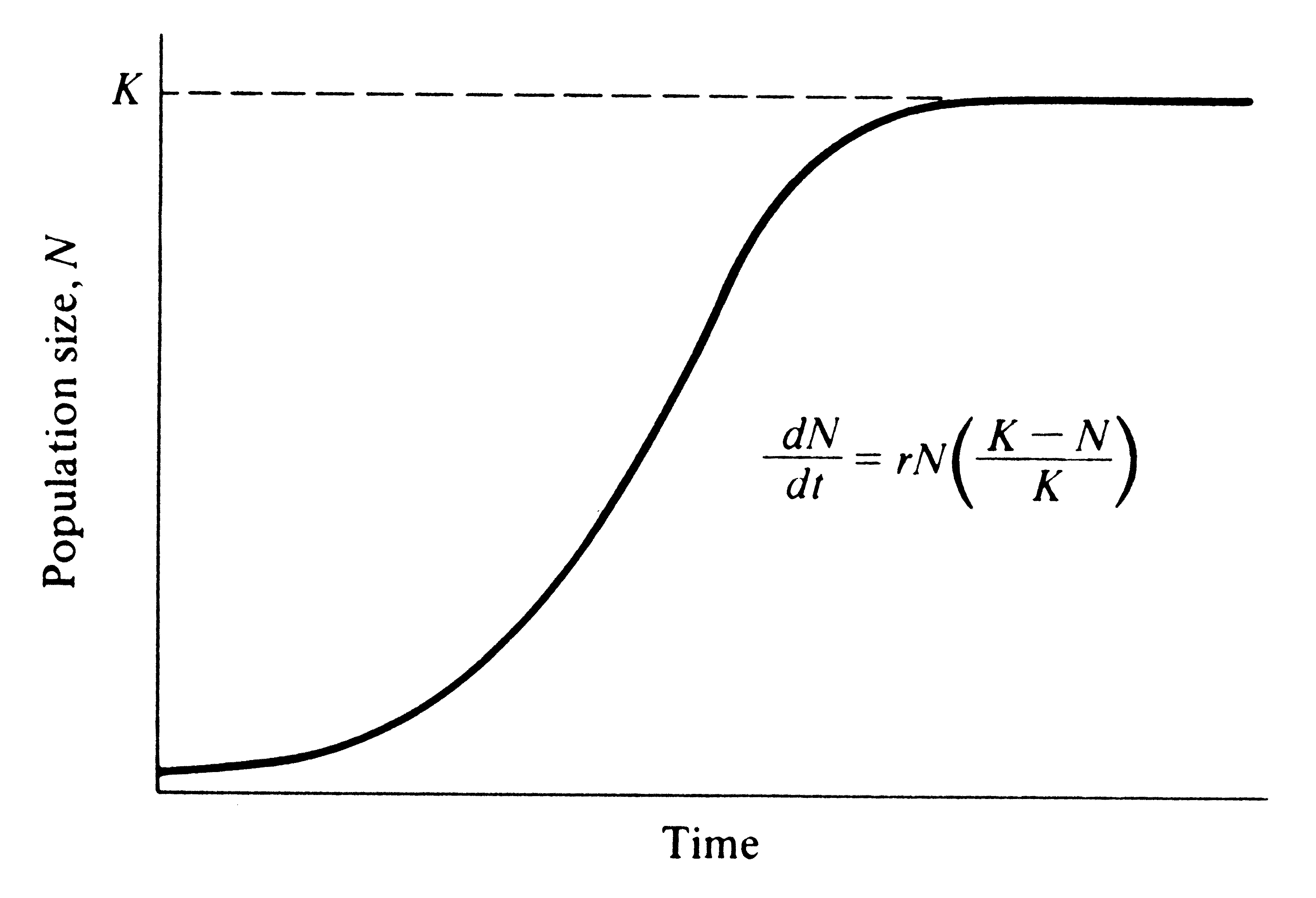
Logistical Growth

• $P(t)$$P(t)$ = population size at time $t$$t$

• $K$$K$ = carrying capacity of the environment

• $P_0$$P_0$ = initial population size

• $r$$r$ = intrinsic rate of increase

• This equation is used for "natural" growth models , where a population grows rapidly at first , but then slows down as it approaches the carrying capacity $K$$K$

• To understand the dynamics of the logistic growth rate at any point in time , we differentiate $P$$P$ with respect to $t$$t$​

• To make life easier , lets define a new variable $A$$A$ to replace most of the terms on the denominator

  • Let $A=\frac{K-P_0}{P_0}\ast e^{-r\ast t}$$A = \frac{K-P_0}{P_0} * e^{-r *t}$

• Now differentiating both sides :

  $$\frac{dP}{dt}=\frac{d}{dt}\left(\frac{K}{1+A}\right)$$

• Pull out constant $K$$K$ :

• Applying Chain Rule :

  • differentiate $\frac{1}{1+A}$$\frac{1}{1 + A}$ with respect to $t$$t$ :

    $$\frac{d}{dt}\left(\frac{1}{1+A}\right)=\frac{d}{dA}\left(\frac{1}{1+A}\right)\ast \frac{d}{dt}$$

  • compute derivative of $\frac{1}{1+A}$$\frac{1}{1+A}$ with respect to $A$$A$ :

    $$\frac{d}{dA}\left(\frac{1}{1+A}\right)=\frac{-1}{{(1+A)}^2}$$

  • substitute $\frac{dA}{dt}$$\frac{dA}{dt}$ and the derivative of $\frac{1}{1+A}$$\frac{1}{1+A}$ into the chain rule formula :

    $$\frac{dP}{dt}=K\ast \left(\frac{-1}{{(1+A)}^2}\right)\ast (-r\ast \left(\frac{K-P_0}{P_0}\right)\ast e^{-r\ast t})$$

  • simplify :

  $$\frac{dP}{dt}=\frac{K\ast r\ast \left(\frac{K-P_0}{P_0}\right)\ast e^{-r\ast t}}{{(1+A)}^2}$$

  • now "un-substitute" stuff for $A$$A$​ back in :

    $$\frac{dP}{dt}=r\ast P\ast (1-\frac{P}{K})$$

  • or written in another way :

  $$\frac{dP}{dt}=r\ast P\ast \left(\frac{K-P}{K}\right)$$

2. The rate of change of bears , $N$$N$ , in a population is directly proportional to $350-N$$350 - N$. Time , $t$$t$ , is measured in years. When $t=0$$t=0$ , the population is $100$$100$ and when $t=2$$t=2$ , the population has increased to $250$$250$​​.

   

   A.) Write and solve a differential equation that describes this scenario.

   • we are going to assume a logistical growth model because the question prompt had "rate of change ...... is directly proportional"

     • this indicates the growth rate is not constant , but rather changes with the size of the population

     • so we are going to use the logistical model instead of any other model ( like exponential )

     • however , we don't need the full original equation that includes a term that represents part of the carrying capacity that is not yet being used : $(1-\frac{P}{K})$$\left(\ 1 - \frac{P}{K} \ \right)$

     • they told us there is a linear/direct relationship in the question prompt between the growth rate and the difference from the maximum limit.

     $$\frac{dN}{dt}=k\ast (350-N)$$

     • this represents a form of the logistic growth rate ,

       • where the growth rate decreases as $N$$N$​ approaches the carrying capcity

       • $k$$k$ = constant of proportionality = determines the rate at which the population's growth rate decreases as it approaches the threshold of 350.

         • reflects how quickly the population approaches the limit

   • so now lets solve $\frac{dN}{dt}=k\ast (350-N)$$\frac{dN}{dt} = k * \left(\ 350 - N \ \right)$ :

     • separate variables / rearrange :

       $$\frac{1}{350-N}\ast dN=k\ast dt$$

     • integrate both sides :

       $$\int (\frac{1}{350-N}\ast dN)=\int (k\ast dt)$$

       • the standard form of the integral $\int (\frac{1}{x}\ast dx)=ln\left|x\right|+C$$\int{\left(\ \frac{1}{x} * dx \ \right) = ln\abs{x} + C}$​

       $$-ln|350-N|=(k\ast t)+C$$

     • solve for $N$$N$ , ( exponentiate both sides to get rid of natural log function ) :

     $$e^{(-ln|350-N|)}=e^{((k\ast t)+C)}$$
     $$350-N=e^{((-k\ast t)-C)}$$
     $$N=350-e^{((-k\ast t)-C)}$$

     • $e^{-C}$$e^{-C}$ is just a constant , so we can pull this out , and lets rename it to just like $C^1$$C^1$

     $$N=350-(C^1\ast e^{(-k\ast t)})$$

     • now we can use the 2 time points we were given to find $k$$k$ and $C^1$$C^1$ :

       • using $t=0$$t=0$ and $N=100$$N=100$ to find $C^1$$C^1$ :

         $$100=350-(C^1\ast e^{(-k\ast 0)})$$
         $$100=350-(C^1\ast e^{\left(0\right)})$$
         $$100=350-(C^1\ast 1.0)$$
         $$C^1=350-100=250$$

         • now that we found $C^1$$C^1$ , substitute it back in :

         $$N=350-(250\ast e^{(-k\ast t)})$$

       • now lets use $t=2$$t = 2$ and $N=250$$N = 250$​ and our newly found $C^1$$C^1$ to find $k$$k$​​ :

         $$250=350-(250\ast e^{(-k\ast 2)})$$

         • solving for $k$$k$ :

         $$100=250\ast e^{(-k\ast 2)}$$
         $$e^{(-k\ast 2)}=\frac{2}{5}$$

         • take natural log of both sides :

         $$-k\ast 2=ln\left(\frac{2}{5}\right)$$

         • simplify ;

           $$k=\frac{-ln\left(\frac{2}{5}\right)}{2}$$

   • Final Solution :

   $$N=350-(250\ast e^{(-\left(\frac{-ln\left(\frac{2}{5}\right)}{2}\right)\ast t)})$$

   B.) Find the bear population in 3 years

   $$N=350-(250\ast e^{(\left(\frac{ln\left(\frac{2}{5}\right)}{2}\right)\ast 3.0)})=286.7544467966324$$

   C.) Find $\underset{t\to \mathrm{\infty }}{lim}N(t)$$\lim\limits_{t \to \infty}{N(t)}$

   • as $t$$t$ approaches infinity , the exponential component $e^{\left((\frac{ln(\frac{2}{5})}{2}\ast t)\right)}$$e^{\left(\ \left(\ \frac{ln(\frac{2}{5})}{2} * t \ \right) \ \right)}$ approaches zero

     • $ln\left(\frac{2}{5}\right)$$ln\left(\ \frac{2}{5} \ \right)$ is negative , because $2/5$$2/5$ is less than $1$$1$

       • multiplying it by any positive number and dividing by 2 keeps it negative

     • $e$$e$ to the power of any negative large number tends towards zero

   • therefore :

   $$\underset{t\to \mathrm{\infty }}{lim}N(t)=350-0=350$$