Sigma Notation $\left(\mathrm{\Sigma }\right)$$\left(\ \Sigma \ \right)$ ( Series )

• $\mathrm{\Sigma }$$\Sigma$ = symbolizes summation

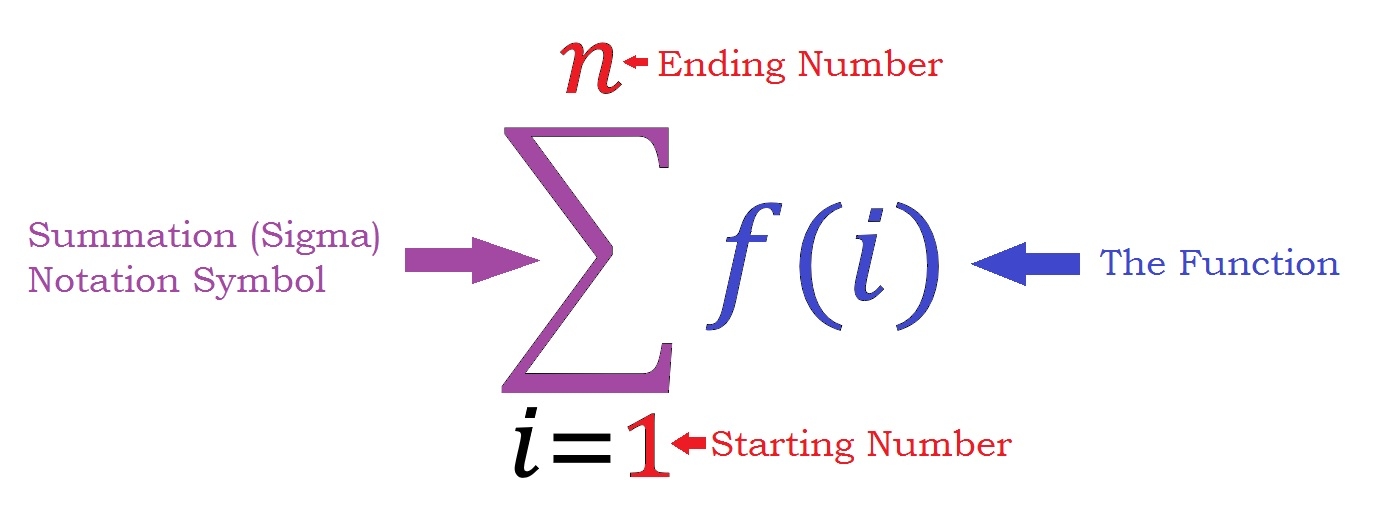
Determine the values of $a$$a$ and $n$$n$ , as well as the general term for $b_k$$b_k$ , in the summation.

• first of all , there seems to be a typo in this question

  • they had it as ${37}^4$$37^{\color{red}{4}}$ , but this is impossible with the other terms listed as a potential series

  • it has to be ${37}^3$$37^{\color{green}{3}}$ for it to make sense as a series

1. Identify any patterns

   • each term has a $37$$37$ term being divided by an integer that increases by $1$$1$ each round

     • there is also a sign flip ( negative to positive ) on each round

2. They just gave us outright the general form for $b_k$$b_k$ .

   • they didn't necessarily have to provide this after the continuation $\dots$$\dots$

     • we could of had to try and determine this structure just by looking at individual terms by themselves in the series.

3. Find Lower Limit $\left(a\right)$$\left(\ a \ \right)$ :

   • the first term in the series they had was $\left(1\right)$$\left(\ 1 \ \right)$

     • really it was $\frac{{37}^0}{1}$$\frac{37^0}{1}$

   • but they just reduced the first term to just being :

   $$\frac{{37}^{1-1}}{1}=\frac{{37}^0}{1}=\frac{1}{1}=1$$

   • the variable renaming gets confusing here

   • but our first term , or the "starting number" in the series HAS to be 1.

   • therefore :

4. Find the Upper Limit $\left(n\right)$$\left(\ n \ \right)$ :

   • they sort of gave us this for free

   • they gave us the equivalent for the last term $\left(b_k\right)$$\left(\ b_k \ \right)$

   $$(-1{)}^{q-1}\ast \frac{{37}^{q-1}}{q}$$

    

   • in that last term , the $37$$37$ in our pattern is being raised to $(q-1)$$\left(\ q - 1 \ \right)$

   • so this last part of the question is really just making sure you understand how sigma notation works in general.

   • the variable renaming can be confusing here again.

   • but the summation is written as starting at a value of $\left(a\right)$$\left(\ a \ \right)$ ,

   • which we know had to be $1$$1$ based on looking at examples in the series

   • and then it ends at $\left(n\right)$$\left(\ n \ \right)$

   $$n=q=\mathrm{\infty }$$

   • just put $n=q$$n = q$ for the answer ,

   • but this is how we can relate the concept of a summation series to calculus

   • if we have some series "at it its limit" or "to infinity"

     $$\sum _{x=1}^{\mathrm{\infty }}(f(x))$$

   • more on this later in the "Moving From Series to Calculus" block

Express the sum using summation notation.

$a$$a$ = ?

$n$$n$ = ?

$b_k$$b_k$ = ?

1. Identify any patterns :

   • each term in the series seems to be in the form of :

   • so this is the generalized form of $b_k$$b_k$

   $$\frac{31+k}{k}$$

2. Find the lower limit $\left(a\right)$$\left(\ a \ \right)$ :

   • think how could we get the first term to just be $32$$32$ by itself :

   • lets assume for a moment $k=a=1$$k = a = 1$

   • that would mean :

3. Find the upper limit $\left(n\right)$$\left(\ n \ \right)$ :

   • the last term in the series was given as :

     $$\frac{31+35}{35}$$

   • you can see it clearly stops at $35$$35$

   • therefore , $n=35$$n = 35$

Moving From Series to Calculus

• Series are used to approximate functions.

  • some functions are complex , and might be impossible to differentiate.

  • you can approximate them by using a series.

• If the series is finite , like :

• Then we can just calculate all of the steps , $x=1$$x=1$ , $x=2$$x=2$ , $x=3$$x=3$

• But If the series is going to infinity :

• Then we have to take the limit

• The derivative of a function = instantaneous rate of change of a function with respect to one of its variables

  • its also a limit

  • the derivative of a function at a specific point = the limit of the average rate of change of the function as the interval of the change approaches zero

Fundamental Theorem of Calculus - Part 1

• Its a connection between the processes of differentiation and integration

• If you have some function $f(x)$$f(x)$

• And it meets these criteria :

  • it is continuous on a finite interval , like between $[a,b]$$\left[\ a\ ,\ b\ \right]$

  • its differentiable everywhere on that finite interval

• Then , the derivative at any of the potential $x$$x$ values inside the interval is the same as the integral

  $$F^{\prime }(x)=\frac{d}{dx}\ast \left[{\int }_a^x(f(t)\ast dt)\right]=f(x)$$

  • $F(x)$$F(x)$ is a new function defined by the integral of $f$

  • The integral ${\int }_a^x(f(t)\ast dt)$$\int^{x}_{a}{\left(\ f(t) * dt \ \right)}$ :

    • accumulates the area under the curve of the function $f(t)$ from $a$$a$ to $x$$x$

  • $t$$t$ is the variable of integration.

    • It's a placeholder that represents the current point of evaluation within the interval from $a$$a$ to $x$$x$

  • $dt$$dt$ indicates that integration is with respect to $t$$t$

• Let the anti-derivative , aka the integral of $f(t)$ = $F(x)$$F(x)$

  • $F(x)={\int }_a^{x}f(t)\ast dt$$F(x) = \int^{x}_{a}{f(t) * dt}$

• Then the derivative of $F(x)$$F(x)$ must be just $f(x)$$f(x)$ :

  • $F^{\prime }(x)=f(x)$$F^{\prime}(x) = f(x)$

Find the derivative using Part 1 of the Fundamental Theorem of Calculus.

• via FTOC Part 1 :

  • we expect to have a variable as one of the limits in the integration

  • the derivative of an integral with respect to its upper limit ,

    • is simply the integrand evaluated at that limit

1. Start with the integral

2. Apply FTOC Part 1

   • Let $F(t) = \int^{t}_{4}{\left(\ 9 * e^x * dx \ \right)}$

   • Then the derivative of $F(t)$$F(t)$ must be just $f(t)$ :

     $$f(t)=9\ast e^t$$

3. Differentiate the integral :

   • the derivative of $F(t)$$F(t)$ with respect to $t$$t$ is just $f(t)$

   • so ,

Find the derivative using Part 1 of the Fundamental Theorem of Calculus.

1. Start with the integral

   $${\int }_1^x(13\ast ln(6\ast u^3)\ast du)$$

2. Apply FTOC Part 1

   • Let $F(x) = \int^{x}_{1}{\left(\ 13 * ln\left(\ 6 * u^3 \ \right) * du \ \right)}$

   • Then the derivative of $F(x)$$F(x)$ must be just $f(x)$$f(x)$ :

   $$f(x)=13\ast ln(6\ast x^3)$$

3. Differentiate the integral :

   • the derivative of $F(x)$$F(x)$ with respect to $x$$x$ is just $f(x)$$f(x)$

   • so ,

   $$\frac{d}{dx}\left[{\int }_1^x(13\ast ln(6\ast u^3)\ast du)\right]=13\ast ln(6\ast x^3)$$

Find the derivative using Part 1 of the Fundamental Theorem of Calculus.

1. Start with the integral

2. Apply FTOC Part 1

   • Let $F(x)={\int }_0^x({(10\ast t^4+3)}^{\frac{4}{5}}\ast dt)$$F(x) = \int^{x}_{0}{\left(\ \left(\ 10 * t^4 + 3 \ \right)^{\frac{4}{5}} * dt \ \right)}$

   • Then the derivative of $F(x)$$F(x)$ must be just $f(x)$$f(x)$ :

     $$f(x)={(10\ast x^4+3)}^{\frac{4}{5}}$$

3. Differentiate the integral :

   • the derivative of $F(x)$$F(x)$ with respect to $x$$x$ is just $f(x)$$f(x)$

   • so ,

   $$\frac{d}{dx}\left[{\int }_0^x({(10\ast t^4+3)}^{\frac{4}{5}}\ast dt)\right]={(10\ast x^4+3)}^{\frac{4}{5}}$$