019 - Glutamate - Glutamine Synaptic Shuttle

Pre-synaptic terminals of glutamatergic neurons retrieve a portion of the glutamate released in response to incoming action potentials
The cell membrane of these terminals contain excitatory amino-acid transporters ( EAAT ) , along with transporters such as Na+/K+-pumps , K+ channels , and likely Na+/H+ exchangers
The coupling stoichiometry of EAAT is cotransport of one glutamate with 3 Na+ and one H+ ,
all in exchange for one K+
You assume that the basal condition of the pre-synaptic terminal under study has the following properties :
$V_m = -65\ mV$
$[Na^+]_e = 145\ mM$
$[Na^+]_i = 10\ mM$
$[K^+]_e = 4.5\ mM$
$[K^+]_i = 150\ mM$
$pH_e = 7.4$
$pH_i = 7.0$
You predict that high synaptic activity will enhance the driving force for glutamate uptake

E_{K} \approx 60 * l o g_{10} (\frac{4.5}{150}) \approx - 91.373 m V

E_{N a} \approx 60 * l o g_{10} (\frac{145}{10}) \approx + 69.682 m V

E_{H} \approx 60 * l o g_{10} (\frac{1 * 10^{- 7.4}}{1 * 10^{- 7.0}}) \approx - 24.0 m V

$V_m$ $pH_i$

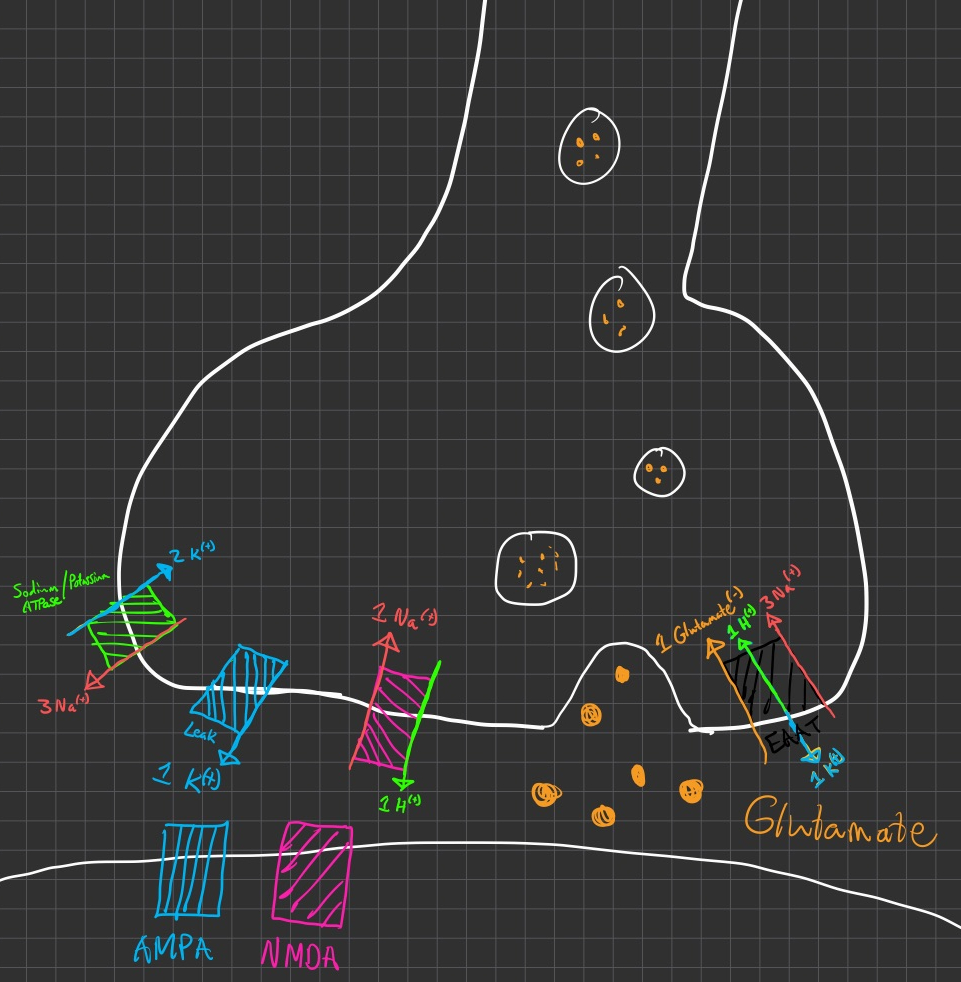
EAAT Net Charge = +2 charges moving inside

$[\text{glutamate}^-]_i = 1\ mM$ $[\text{glutamate}^-]_e = 25\ nM$

E_{G l u} \approx - 60 * l o g_{10} (\frac{25 * 10^{- 9}}{1 * 10^{- 3}}) \approx + 276.12 m V

For the resting condition , calculate the driving force for EAAT ( and flow direction )

Ion	$mV$	$n$	$z$	$n * z * \left(\ E - V_m \ \right)$ $mV$ )
Na	$+69.7$	3	+1	$3 * 1 * \left(\ 69.7 - \left(\ -65 \ \right) \ \right) = 404.10$
K	$-91.4$	1	+1	$1 * 1 * \left(\ -91.4 - \left(\ -65 \ \right) \ \right) = -26.40$
H	$-24.0$	1	+1	$1 * 1 * \left(\ -24.0 - \left(\ -65 \ \right) \ \right) = +41.0$
Glutamate	$+276.12$	1	-1	$1 * -1 * \left(\ +276.12 - \left(\ -65 \ \right) \ \right) = -341.12$
$V_m$	$-65.0$	1	+2

Total = (404.10) + (- 26.40) + (41.0) + (- 341.12) = + 77.580 m V

Calculate the driving force for EAAT at the peak of an incoming action potential

$V_m = +55\ mV$

Ion	$mV$	$n$	$z$	$n * z * \left(\ E - V_m \ \right)$ $mV$ )
Na	$+69.7$	3	+1	$3 * 1 * \left(\ 69.7 - \left(\ +55 \ \right) \ \right) = 44.10$
K	$-91.4$	1	+1	$1 * 1 * \left(\ -91.4 - \left(\ +55 \ \right) \ \right) = -146.40$
H	$-24.0$	1	+1	$1 * 1 * \left(\ -24.0 - \left(\ +55 \ \right) \ \right) = -79.0$
Glutamate	$+276.12$	1	-1	$1 * -1 * \left(\ +276.12 - \left(\ +55 \ \right) \ \right) = -221.12$

Total = (44.10) + (- 146.40) + (- 79.0) + (- 221.12) = - 402.42 m V

$[\text{glutamate}^-]_i = 1\ mM$ $[\text{glutamate}^-]_e = 1\ mM$

E_{G l u} = - 60 * l o g_{10} (\frac{1}{1}) = 0 m V

Calculate the driving force for EAAT during these inter-spike periods and at the peaks of these action potentials

Inter-Spike Periods

Ion	$mV$	$n$	$z$	$n * z * \left(\ E - V_m \ \right)$ $mV$ )
Na	$+69.7$	3	+1	$3 * 1 * \left(\ 69.7 - \left(\ -65 \ \right) \ \right) = 404.10$
K	$-91.4$	1	+1	$1 * 1 * \left(\ -91.4 - \left(\ -65 \ \right) \ \right) = -26.40$
H	$-24.0$	1	+1	$1 * 1 * \left(\ -24.0 - \left(\ -65 \ \right) \ \right) = +41.0$
Glutamate	$0$	1	-1	$1 * -1 * \left(\ 0 - \left(\ -65 \ \right) \ \right) = -65.0$

Total = (404.10) + (- 26.40) + (+ 41.0) + (- 65.0) = + 353.70 m V

At Action Potential Peak

Ion	$mV$	$n$	$z$	$n * z * \left(\ E - V_m \ \right)$ $mV$ )
Na	$+69.7$	3	+1	$3 * 1 * \left(\ 69.7 - \left(\ +55 \ \right) \ \right) = 44.10$
K	$-91.4$	1	+1	$1 * 1 * \left(\ -91.4 - \left(\ +55 \ \right) \ \right) = -146.40$
H	$-24.0$	1	+1	$1 * 1 * \left(\ -24.0 - \left(\ +55 \ \right) \ \right) = -79.0$
Glutamate	$0$	1	-1	$1 * -1 * \left(\ 0 - \left(\ +55 \ \right) \ \right) = +55$

Total = (44.10) + (- 146.40) + (- 79.0) + (+ 55.0) = - 126.30 m V

$[\text{glutamate}^-]_i = 1\ mM$ $[\text{glutamate}^-]_e = 3\ \mu M$ $[Na^+]_i = 60\ mM$ $[Na^+]_e = 135\ mM$ $pH_i = 6.5$ $pH_e = 6.5$ $V_m = -20\ mV$

Determine the reversal potential for EAAT during these hypoxic conditions.

E_{G l u} \approx - 60 * l o g_{10} (\frac{3 * 10^{- 6}}{1 * 10^{- 3}}) \approx + 151.37 m V

E_{N a} \approx 60 * l o g_{10} (\frac{135}{60}) \approx + 21.131 m V

E_{H} = 60 * l o g_{10} (\frac{1 * 10^{- 6.5}}{1 * 10^{- 6.5}}) = 0 m V

Ion	$mV$	$n$	$z$	$n * z * \left(\ E - V_m \ \right)$ $mV$ )
Na	$+21.131$	3	+1	$3 * 1 * \left(\ 21.131 - \left(\ V_{rev} \ \right) \ \right) =\ ?$
K	$-91.4$	1	+1	$1 * 1 * \left(\ -91.4 - \left(\ V_{rev} \ \right) \ \right) =\ ?$
H	$0$	1	+1	$1 * 1 * \left(\ 0 - \left(\ V_{rev} \ \right) \ \right) =\ ?$
Glutamate	$+151.37$	1	-1	$1 * -1 * \left(\ +151.37 - \left(\ V_{rev} \ \right) \ \right) =\ ?$

V_{r e v} = 0 = (3 * 1 * ((21.131) - (V_{r e v}))) + (1 * 1 * ((- 91.4) - (V_{r e v}))) + (1 * 1 * ((0) - (V_{r e v}))) + (1 * - 1 * ((151.37) - (V_{r e v})))

V_{r e v} = \frac{(3 * E_{N a}) + (E_{H}) + (- E_{G l u}) + (E_{K})}{6}

V_{r e v} = \frac{(3 * 21.131) + (0) + (- (151.37)) + (- 91.4)}{6} = - 29.896 m V

Astrocytes adjacent to pre-synaptic terminals of glutamatergic neurons also retrieve a portion of the glutamate released in response to incoming action potentials.
These astrocytes convert glutamate to glutamine and then extrude glutamine for retrieval by pre-synaptic terminals ( glutamine-shuttle ) , such that post-synaptic glutamate receptors remain unaware
Cell membranes of these astrocytes contain Na+-dependent neutral amino-acid transporters ( SNAT3 ) , along with transporters such as Na+/K+ pumps , K+ channels , and likely others
The coupling stoichiometry of SNAT3 is cotransport of one glutamine with one Na+ in exchange for one H+
Cell membranes of these pre-synaptic terminals contain SNAT1
The coupling stoichiometry of SNAT1 is cotransport of one glutamine with one Na+
You assume that for the synaptic locale under study , the basal condition has the following properties :
$V_m = -65\ mV$
$[Na^+]_e = 145\ mM$
$[Na^+]_i = 11.0\ mM$
$[K^+]_e = 4.5\ mM$
$[K^+]_i = 150\ mM$
$pH_e = 7.4$
$pH_i^A = 7.2$
$[\text{glutamate}^-]_e = 25\ \mu M$
$[\text{glutamate}^-]_i^A = 1.2\ mM$
$[\text{glutamate}^-]_i^N = 0.3\ mM$
You predict that extracellular glutamine concentrations will remain in a narrow range that supports continual glutamine uptake by the pre-synaptic terminal

E_{N a} \approx 60 * l o g_{10} (\frac{145}{11}) \approx + 67.199 m V

E_{K} \approx 60 * l o g_{10} (\frac{4.5}{150}) \approx - 91.373 m V

E_{H} \approx 60 * l o g_{10} (\frac{1 * 10^{- 7.4}}{1 * 10^{- 7.2}}) \approx - 12.0 m V

E_{G l u}^{A} = - 60 * l o g_{10} (\frac{25 * 10^{- 6}}{1.2 * 10^{- 3}}) = + 100.87 m V

E_{G l u}^{N} = - 60 * l o g_{10} (\frac{25 * 10^{- 6}}{0.3 * 10^{- 3}}) = + 64.751 m V

Draw a diagram of the synaptic locale that includes SNAT and the other transporters and enzymes needed to achieve a glutamate re-supply for the pre-synaptic terminal

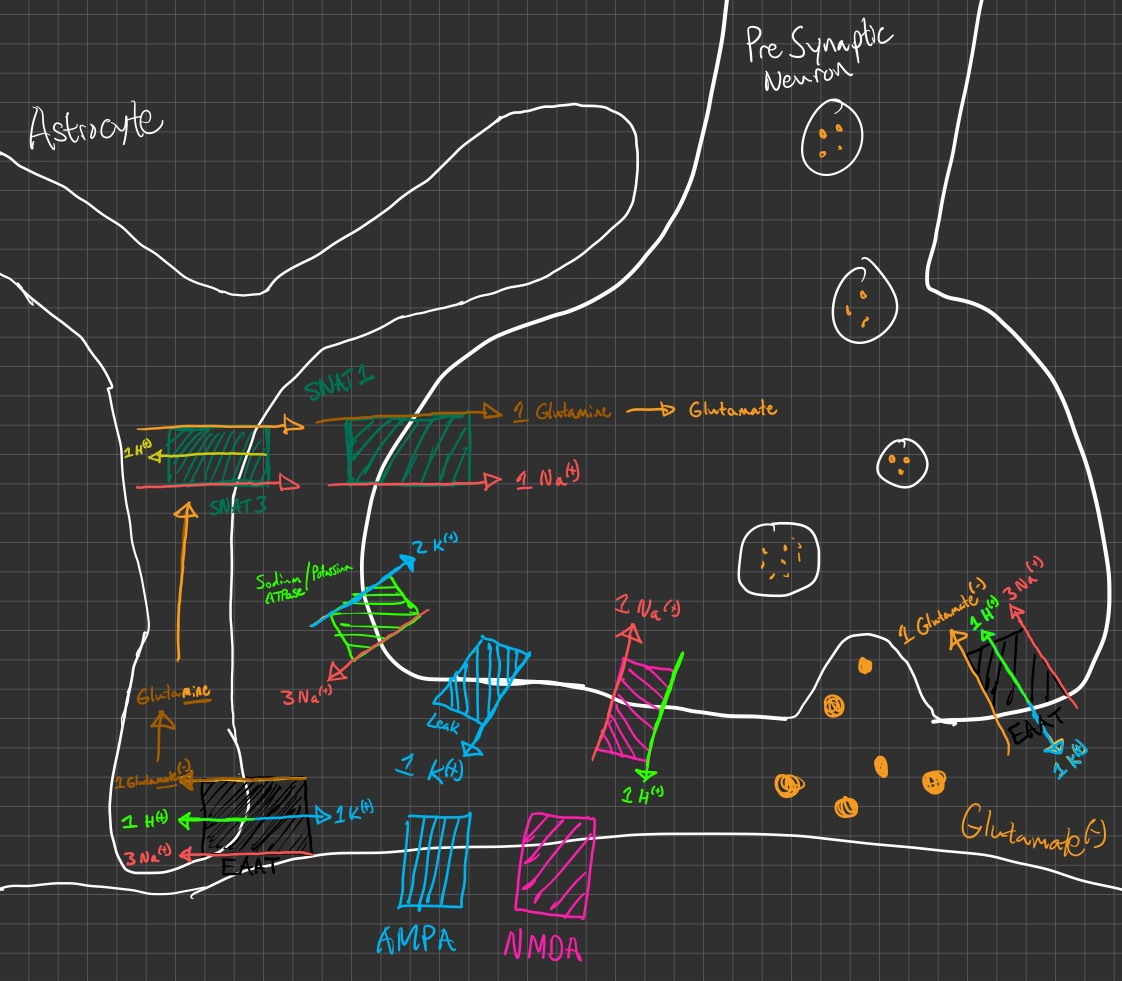
Calculate the driving force for SNAT1 and for SNAT3 during the inter-spike periods

SNAT1

Ion	$mV$	$n$	$z$	$\left(\ E - V_m \ \right)$ $mV$ )	$n * z * DF$ $mV$ )
Na	$+67.199$	1	+1	$\left(\ +67.199 \ \right) - \left(\ -65 \ \right) = 132.20$	$1 * 1 * 132.20 = 132.20$
Glutamine	?	1	0	$\left(\ 0 \ \right) - \left(\ -65 \ \right) = -65$	$1 * 0 * -65 = 0.0$

Total = (132.20) + (0) = + 132.20 m V

SNAT3

Ion	$mV$	$n$	$z$	$\left(\ E - V_m \ \right)$ $mV$ )	$n * z * DF$ $mV$ )
Na	$+67.199$	1	+1	$\left(\ +67.199 \ \right) - \left(\ -65 \ \right) = 132.20$	$1 * 1 * 132.20 = 132.20$
H	$-12.0$	1	+1	$\left(\ -12 \ \right) - \left(\ -65 \ \right) = 53.0$	$1 * 1 * 53.0 = 53.0$
Glutamine	?	1	0	$\left(\ 0 \ \right) - \left(\ -65 \ \right) = -65$	$1 * 0 * -65 = 0.0$

Total = (132.20) + (53) + (0) = + 185.20 m V

Calculate the driving force for SNAT1 and for SNAT3 at the peak of an incoming action potential

$V_m = +55\ mV$

SNAT1

Ion	$mV$	$n$	$z$	$\left(\ E - V_m \ \right)$ $mV$ )	$n * z * DF$ $mV$ )
Na	$+67.199$	1	+1	$\left(\ +67.199 \ \right) - \left(\ +55 \ \right) = 12.199$	$1 * 1 * 12.199 = 12.199$
Glutamine	?	1	0	$\left(\ 0 \ \right) - \left(\ +55 \ \right) = +55$	$1 * 0 * +55 = 0.0$

Total = (12.199) + (0) = + 12.199 m V

SNAT3

Ion	$mV$	$n$	$z$	$\left(\ E - V_m \ \right)$ $mV$ )	$n * z * DF$ $mV$ )
Na	$+67.199$	1	+1	$\left(\ +67.199 \ \right) - \left(\ +55 \ \right) = 12.199$	$1 * 1 * 12.199 = 12.199$
H	$-12.0$	1	+1	$\left(\ -12 \ \right) - \left(\ +55 \ \right) = -67.0$	$1 * 1 * -67.0 = -67.0$
Glutamine	?	1	0	$\left(\ 0 \ \right) - \left(\ +55 \ \right) = +55$	$1 * 0 * +55 = 0.0$

Total = (12.199) + (- 67.0) + (0) = - 54.801 m V

$[\text{glutamine}]_e$ $[\text{glutamine}]_e$ changes )

SNAT1

Ion	$mV$	$n$	$z$	$\left(\ E - V_m \ \right)$ $mV$ )	$n * z * DF$ $mV$ )
Na	$+67.199$	1	+1	$\left(\ +67.199 \ \right) - \left(\ -65\ \right) = 132.20$	$1 * 1 * 132.20 = 132.20$
Glutamine	?	1	0	$\left(\ ? \ \right) - \left(\ -65 \ \right) =\ ?$	$1 * 0 *\ ? =\ ?$

0 = (132.20) + ((E_{G l n} - (- 65)))

E_{G l n} = - 197.20

- 197.20 = 60 * l o g_{10} (\frac{[glutamine]_{e}}{[glutamine]_{i}})

[glutamine]_{e} = 5.1681 * 10^{- 4} M

SNAT3

Ion	$mV$	$n$	$z$	$\left(\ E - V_m \ \right)$ $mV$ )	$n * z * DF$ $mV$ )
Na	$+67.199$	1	+1	$\left(\ +67.199 \ \right) - \left(\ -65 \ \right) = 132.20$	$1 * 1 * 132.20 = 132.20$
H	$-12.0$	1	+1	$\left(\ -12 \ \right) - \left(\ -65 \ \right) = 53.0$	$1 * 1 * 53.0 = 53.0$
Glutamine	?	1	0	$\left(\ ? \ \right) - \left(\ -65 \ \right) =\ ?$	$1 * 0 *\ ? =\ ?$

0 = (132.20) + (53.0) + ((E_{G l n} - (- 65)))

E_{G l n} = - 250.20

- 250.20 = 60 * l o g_{10} (\frac{[glutamine]_{e}}{[glutamine]_{i}})

[glutamine]_{e} = 6.7608 * 10^{- 5} M

$[\text{glutamate}^-]_i = 1\ mM$ $[\text{glutamate}^-]_e = 30\ \mu M$ $[Na^+]_i = 60\ mM$ $[Na^+]_e = 135\ mM$ $[K^+]_i = 100\ mM$ $[K^+]_e = 15\ mM$ $pH_i = 6.5$ $pH_e = 6.5$ $V_m = -20\ mV$

$[\text{glutamine}]_e$ that allows the glutamine-shuttle to operate during these hypoxic conditions.

E_{N a} \approx 60 * l o g_{10} (\frac{135}{60}) \approx + 21.131 m V

E_{K} \approx 60 * l o g_{10} (\frac{15}{100}) \approx - 49.435 m V

E_{H} \approx 60 * l o g_{10} (\frac{1 * 10^{- 6.5}}{1 * 10^{- 6.5}}) \approx 0.0 m V

E_{G l u} = - 60 * l o g_{10} (\frac{30 * 10^{- 6}}{1 * 10^{- 3}}) = + 91.373 m V

D F_{N a} = (21.131) - (- 20) = + 41.131 m V

SNAT 1

0 = (41.131) + ((E_{G l n} - (- 20)))

E_{G l n} = - 61.131

- 61.131 = 60 * l o g_{10} (\frac{[glutamine]_{e}}{[glutamine]_{i}})

[glutamine]_{e} = 0.095752 M

SNAT 3

0 = (41.131) + ((0 - (- 20))) + ((E_{G l n} - (- 20)))

E_{G l n} = - 81.131

- 81.131 = 60 * l o g_{10} (\frac{[glutamine]_{e}}{[glutamine]_{i}})

[glutamine]_{e} = 0.046183 M