• You’ve become interested in the $N{a}^{+}/C{a}^{+2}$$Na^+/Ca^{+2}$ -exchanger and its orientation of flow during the action potential in mammalian cardiac muscle cells.

• You begin by assuming that the resting condition ( between action potentials ) has the following properties ( based on reported findings ) :

  • $[N{a}^{+}{]}_e=145mM$$[\ Na^+\ ]_e = 145\ mM$

  • $[N{a}^{+}{]}_i=8mM$$[\ Na^+\ ]_i = 8\ mM$

  • $[C{a}^{+2}{]}_e=1.2mM$$[\ Ca^{+2}\ ]_e = 1.2\ mM$

  • $[C{a}^{+2}{]}_i=0.09\mu M$$[\ Ca^{+2}\ ]_i = 0.09\ \mu M$

  • $V_m=-82mV$$V_m = -82\ mV$

• The cardiac action potential leads to increased cytosolic free $C{a}^{+2}$$Ca^{+2}$ that promotes contraction.

• NCK :

  • If $\frac{\mathrm{\Delta }u}{F}<0$$\frac{\Delta u}{F} < 0$ , then 3 Na in , and 1 Ca out

  • If $\frac{\mathrm{\Delta }u}{F}>0$$\frac{\Delta u}{F} > 0$ , then 3 Na out , and 1 Ca in

1. Calculate the driving force for the $N{a}^{+}/C{a}^{+2}$$Na^+/Ca^{+2}$ -exchanger ( $\mathrm{\Delta }\mu /F$$\Delta \mu/F$ ) during rest

   

   $$E_{Na}=60\ast lo{g}_{10}\left(\frac{145}{8}\right)=75.497mV$$
   $$E_{Ca}=\frac{60}{2}\ast lo{g}_{10}\left(\frac{1.2\ast {10}^{-3}}{0.09\ast {10}^{-6}}\right)=123.75mV$$
   $$D{F}_{Na}=(-82)-\left(75.497\right)=-157.50mV$$
   $$D{F}_{Ca}=2\ast ((-82)-\left(123.75\right))=-411.50mV$$

   • we know 3 sodium ions are entering the cytosol for every 1 calcium ion exported

     • we make Ca driving force positive , because its leaving

     • and we make Na negative , because its entering

   $$D{F}_{N{a}^{+}/C{a}^{+2}}=(3\ast (-157.50))+(1\ast \left(411.50\right))=-61mV$$

   • you can also do it like this :

     $$3\ast RT\ast ln\left(\frac{[Na{]}_i}{[Na{]}_o}\right)=1\ast RT\ast ln\left(\frac{[Ca{]}_o}{[Ca{]}_i}\right)$$
   $$\frac{\mathrm{\Delta }\mu }{F}=60\ast lo{g}_{10}\left(\frac{{([N{a}^{+}{]}_i)}^3\ast ([C{a}^{+2}{]}_o)}{{([N{a}^{+}{]}_o)}^3\ast ([C{a}^{+2}{]}_i)}\right)+V_m$$
   $$\frac{\mathrm{\Delta }\mu }{F}=60\ast lo{g}_{10}\left(\frac{{(8\ast {10}^{-3})}^3\ast (1.2\ast {10}^{-3})}{{(145\ast {10}^{-3})}^3\ast (0.09\ast {10}^{-6})}\right)+(-82)=-60.994mV$$

2. Mark this value on a sketch plot of driving force ( y-axis ) vs $V_m$$V_m$ ( x-axis )

   

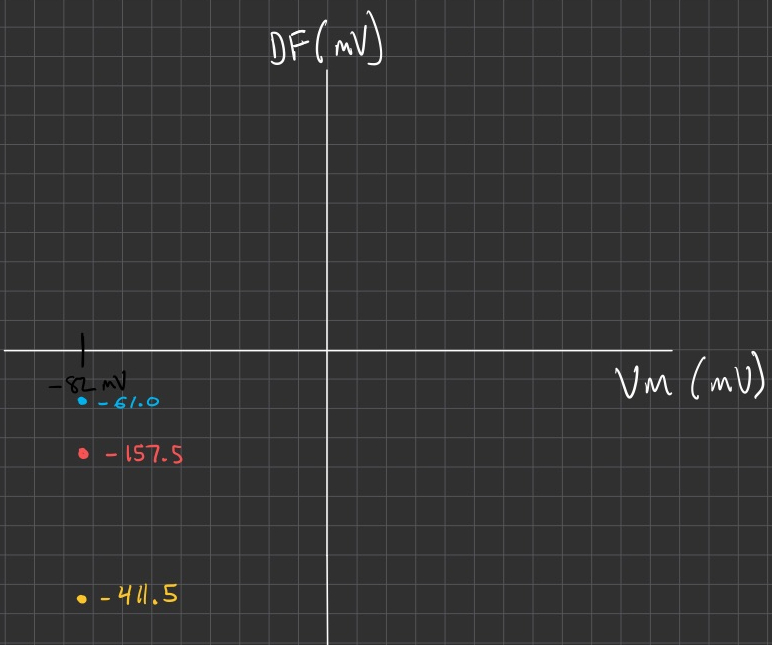
• The action potential peaks at $V_m=+40mV$$V_m= +40\ mV$ , then declines to $V_m=+35mV$$V_m = +35\ mV$ at peak $C{a}^{+2}$$Ca^{+2}$

  • with $[C{a}^{+2}{]}_i=6.5\mu M$$[\ Ca^{+2}\ ]_i = 6.5\ \mu M$ and $[N{a}^{+}{]}_i=12mM$$[\ Na^+\ ]_i = 12\ mM$

3. Calculate the driving force for the exchanger at peak $C{a}^{+2}$$Ca^{+2}$

   $$\frac{\mathrm{\Delta }\mu }{F}=60\ast lo{g}_{10}\left(\frac{{(12\ast {10}^{-3})}^3\ast (1.2\ast {10}^{-3})}{{(145\ast {10}^{-3})}^3\ast (6.5\ast {10}^{-6})}\right)+(+35)=-23.818mV$$

4. Calculate the driving force at the peak of the action potential , if only $V_m$$V_m$ changed

   $$\frac{\mathrm{\Delta }\mu }{F}=60\ast lo{g}_{10}\left(\frac{{(8\ast {10}^{-3})}^3\ast (1.2\ast {10}^{-3})}{{(145\ast {10}^{-3})}^3\ast (0.09\ast {10}^{-6})}\right)+(+40)=61.006mV$$

• During the action potential plateau :

  • $V_m=+20mV$$V_m = +20\ mV$

  • $[N{a}^{+}{]}_i=8mM$$[\ Na^+\ ]_i = 8\ mM$

  • $[C{a}^{+2}{]}_i=0.8\mu M$$[\ Ca^{+2}\ ]_i = 0.8\ \mu M$

5. Calculate the driving force for the exchanger at this mid plateau point

   $$\frac{\mathrm{\Delta }\mu }{F}=60\ast lo{g}_{10}\left(\frac{{(8\ast {10}^{-3})}^3\ast (1.2\ast {10}^{-3})}{{(145\ast {10}^{-3})}^3\ast (0.8\ast {10}^{-6})}\right)+(+20)=-15.925mV$$

• At the end of the action potential plateau :

  • $V_m=0mV$$V_m = 0\ mV$

  • $[N{a}^{+}{]}_i=8mM$$[\ Na^+\ ]_i = 8\ mM$

  • $[C{a}^{+2}{]}_i=0.5\mu M$$[\ Ca^{+2}\ ]_i = 0.5\ \mu M$

6. Calculate the driving force for the exchanger at the end of the plateau

   $$\frac{\mathrm{\Delta }\mu }{F}=60\ast lo{g}_{10}\left(\frac{{(8\ast {10}^{-3})}^3\ast (1.2\ast {10}^{-3})}{{(145\ast {10}^{-3})}^3\ast (0.5\ast {10}^{-6})}\right)+\left(0\right)=-23.677mV$$

    

7. Using your graph you determine the time period of the action potential during which the $N{a}^{+}/C{a}^{+2}$$Na^+/Ca^{+2}$ -exchanger produces $C{a}^{+2}$$Ca^{+2}$ influx

   • asdf

• The cardiac glycoside digitalis inhibits the $N{a}^{+}/K^{+}$$Na^+/K^+$-pump ,

• If a clinical dose is given , it increases $[N{a}^{+}{]}_i$$[\ Na^+\ ]_i$ to $12mM$$12\ mM$ for a new resting condition

8. Determine how this elevated $[N{a}^{+}{]}_i$$[\ Na^+\ ]_i$ alters the orientation of exchanger flow during the action potential. ( assume that $V_m$$V_m$ and $[C{a}^{+2}{]}_i$$[\ Ca^{+2}\ ]_i$ follow a similar time course as in the absence of the inhibitor )

   • rest :

     $$\frac{\mathrm{\Delta }\mu }{F}=60\ast {\log }_{10}\left(\frac{(12\ast {10}^{-3}{)}^3\ast (1.2\ast {10}^{-3})}{(145\ast {10}^{-3}{)}^3\ast (0.09\ast {10}^{-6})}\right)+(-82)=-29.297mV$$

   • action potential peak :

     $$\frac{\mathrm{\Delta }\mu }{F}=60\ast {\log }_{10}\left(\frac{(12\ast {10}^{-3}{)}^3\ast (1.2\ast {10}^{-3})}{(145\ast {10}^{-3}{)}^3\ast (0.09\ast {10}^{-6})}\right)+(40)=92.703mV$$

   • peak Ca :

     $$\frac{\mathrm{\Delta }\mu }{F}=60\ast {\log }_{10}\left(\frac{(12\ast {10}^{-3}{)}^3\ast (1.2\ast {10}^{-3})}{(145\ast {10}^{-3}{)}^3\ast (6.5\ast {10}^{-6})}\right)+(35)=-23.818mV$$

   • plateau :

     $$\frac{\mathrm{\Delta }\mu }{F}=60\ast {\log }_{10}\left(\frac{(12\ast {10}^{-3}{)}^3\ast (1.2\ast {10}^{-3})}{(145\ast {10}^{-3}{)}^3\ast (0.8\ast {10}^{-6})}\right)+(20)=15.772mV$$

   • end of plateau :

   $$\frac{\mathrm{\Delta }\mu }{F}=60\ast {\log }_{10}\left(\frac{(12\ast {10}^{-3}{)}^3\ast (1.2\ast {10}^{-3})}{(145\ast {10}^{-3}{)}^3\ast (0.5\ast {10}^{-6})}\right)+(0)=8.0191mV$$

    

   • Inhibiting $N{a}^{+}/K^{+}$$Na^+/K^+$-pump ➡️ increases $[N{a}^{+}{]}_i$$[\ Na^+\ ]_i$ ➡️ loss of sodium gradient ➡️ driving force to run NCX force becomes less negative ➡️ less calcium export ➡️ more intracellular calcium ➡️ stronger muscle contractions