Table 2.1 - Ionic Composition of a Typical Cell

• 3 , 2 , 1 , NOKIA

• Therefore :

  • B = outside ( destination )

  • A = inside ( origin )

( 8.314 * ( 29 + 273.15 ) * math.log( 150 / 4.5 ) ) + ( 1 * 96485 * ( ( -0.065 ) - ( 0 ) ) )

Epithelial cell transport function

Epithelial cells maintain an intracellular composition distinct from the extracellular ( interstitial ) space, just as other cells do. In part, these composition differences are needed to ensure cellular homeostasis. Epithelial cells also use the ion concentration gradients and membrane electrical potential differences ( PD ) to achieve net transport of solutes and water in absorptive or secretory directions. Typical values for ion concentrations in epithelial cells are shown in the table, together with Nernst potentials for each ( inside of the cell with respect to the outside of the cell ).

1. What accounts for the apparent relative lack of anions in the intracellular space?

   • The apparent deficiency of small inorganic anions like Cl⁻ and HCO₃⁻ in the intracellular space is balanced by the presence of large, negatively charged molecules that are abundant within the cell. These include:

     • Nucleic Acids (DNA and RNA): DNA and RNA molecules have phosphate groups along their backbones, which carry negative charges. These macromolecules are confined inside the cell nucleus (DNA) and cytoplasm (RNA) and contribute significantly to the cell's overall negative charge.

     • Organic Phosphates: Molecules such as ATP, ADP, and various metabolic intermediates contain phosphate groups and are negatively charged. They are present in high concentrations within the cell and play crucial roles in energy transfer and metabolism.

     • Proteins: Many intracellular proteins have negatively charged amino acid residues (like aspartate and glutamate), adding to the negative charge inside the cell.

     • Phospholipids in the Cell Membrane: While animal cells do not have a cell wall, the plasma membrane's inner leaflet contains phospholipids with negatively charged head groups, such as phosphatidylserine and phosphatidylinositol. These contribute to the negative charge on the cytoplasmic side of the membrane and influence interactions with intracellular proteins.

   • These large, impermeant anionic molecules are not typically included in tables listing ionic compositions because they do not freely move across the cell membrane. Their negative charges balance the positive charges of intracellular cations like K⁺, maintaining electrical neutrality within the cell. Despite the lower measured concentrations of small anions, the presence of these large negatively charged molecules explains the apparent relative lack of small anions in the intracellular space.

2. What distinguishes the intracellular composition of epithelial cells compared with a typical cell ( Table 2-1 ) ?

   • Higher Intracellular Cl⁻ Concentration: Epithelial cells often have a higher intracellular Cl⁻ concentration (39 mM) compared to typical cells (20–30 mM). This elevated Cl⁻ level facilitates Cl⁻ transport across the epithelial layer, which is crucial for processes like fluid secretion in the gastrointestinal tract.

   • Ion Transport Mechanisms: Epithelial cells express specific ion channels, transporters, and pumps that adjust their intracellular ion concentrations to drive directional transport of substances. For instance, they may have enhanced activity of Na⁺/K⁺ ATPases, Cl⁻ channels, or other ion exchangers not as prominently featured in typical cells.

   • Membrane Potential Dynamics: The differences in ion concentrations affect the Nernst potentials and thus the electrochemical gradients, influencing the membrane potential and the cell's ability to transport ions and water effectively.

3. Predict the range of membrane electrical PD ( from cell negative to cell positive ) that could be generated by a cell having the composition in the table.

   • Maximum Negative Vₘ: If the membrane is predominantly permeable to K⁺, the membrane potential would approach the Nernst potential for K⁺, which is –91 mV. This represents the largest negative PD the cell could generate under these conditions.

   • Maximum Positive Vₘ: If the membrane becomes highly permeable to Ca²⁺, the membrane potential would move toward the Nernst potential for Ca²⁺, which ranges from +95 to +156 mV. This range represents the largest positive PD achievable, considering the variability in intracellular Ca²⁺ concentration.

   • Overall Range: Therefore, the membrane potential could range from approximately –91 mV to +156 mV, depending on which ion channels are open and the membrane's permeability to those ions.

4. Indicate the type of ion channels that would be required to obtain the largest negative and largest positive membrane electrical PD ( $V_m$$V_m$ )

   • Largest Negative Vₘ (Hyperpolarization): To achieve the most negative membrane potential, the cell would need to increase its permeability to K⁺ ions. This can be accomplished by opening K⁺ channels (such as inward-rectifier potassium channels). As K⁺ ions move out of the cell down their concentration gradient, the inside of the cell becomes more negative, driving the membrane potential toward the K⁺ Nernst potential (–91 mV).

   • Largest Positive Vₘ (Depolarization): To reach the most positive membrane potential, the cell must increase its permeability to Ca²⁺ ions. Opening Ca²⁺ channels (such as voltage-gated calcium channels) allows Ca²⁺ ions to flow into the cell due to their high extracellular concentration and positive Nernst potential (+95 to +156 mV). This influx of positive charge depolarizes the cell, pushing the membrane potential toward the Nernst potential for Ca²⁺.

• Transepithelial absorption of Na+ in the distal portion of the large intestine is electrogenic, occurring via the Koefoed-Johnsen & Ussing cellular mechanism.

• This electrogenic absorption is produced by Na+ / K+ exchange pumps and K+ channels in the basolateral membrane together with apical membrane Na+ channels.

• Draw a diagram for an epithelial cell containing these transport components.

  • asdf

• During steady-state electrogenic Na+ absorption, the transepithelial electrical PD ( $V_{te}$$V_{te}$ ) is -40 mV ( lumen with respect to interstitium )

• and the basolateral membrane electrical PD ( $V_b$$V_b$ ) is -65 mV ( intracellular with respect to interstitium )

• based on experimental measurements.

• The corresponding apical membrane electrical PD ( $V_a$$V_a$ ) is -25 mV ( intracellular with respect to lumen ).

• Initially , the lumen is assumed to have the same composition as the interstitial space.

1. Determine the total electrochemical driving force acting on Na+ flow through the apical membrane Na+ conductance $g_a^{Na}$$g_a^{Na}$

   $$E_{Na}=\frac{60}{+1}\ast lo{g}_{10}\left(\frac{145}{10}\right)=69.68208013409848mV$$
   $$\text{Driving Force}=(-25mV)-\left(69.68208013409848mV\right)=-94.68208013409848mV$$

   • Driving Force = negative

     • therefore think of the inside as being negative

     • Sodium is positively charged

       • therefore , it will want to enter the cell

2. Determine the total electrochemical driving force acting on K+ flow through the apical membrane K+ conductance $g_b^K$$g_b^{K}$

   $$E_K=\frac{60}{+1}\ast lo{g}_{10}\left(\frac{4.5}{150}\right)=-91.37272471682026mV$$
   $$\text{Driving Force}=(-25mV)-(-91.37272471682026mV)=66.37272471682026mV$$

   • Driving Force = positive

     • therefore think of the inside as being positive

     • Potassium is positively charged

       • therefore , it will want to leave the cell

3. Assuming the stoichiometry of the Na+/K+ exchange pumps is 3Na+ : 2K+ :

   • determine the electrochemical energy needed to pump Na+ out and K+ in.

     • For Na+ moving from inside to outside :

     $$\mathrm{\Delta }{G}_{Na}=(\frac{8.314J}{mol\cdot K^{\circ }}\ast (29C^{\circ }+273.15K^{\circ })\ast ln\left(\frac{\text{145 mM}}{\text{10 mM}}\right))+((+1)\ast \frac{96485J}{Volts\cdot mol}\ast (\left(0V\right)-(-0.065V)))=\frac{12989.187235923013J}{mol}$$
     $$\mathrm{\Delta }{G}_{\text{total Na}}=3\ast \frac{12989.187235923013J}{mol}=\frac{38967.56170776904J}{mol}$$

     • For K+ moving from outside to inside :

     $$\mathrm{\Delta }{G}_K=(\frac{8.314J}{mol\cdot K^{\circ }}\ast (29C^{\circ }+273.15K^{\circ })\ast ln\left(\frac{\text{150 mM}}{\text{4.5 mM}}\right))+((+1)\ast \frac{96485J}{Volts\cdot mol}\ast ((-0.065V)-\left(0V\right)))=\frac{2537.2117805658827J}{mol}$$
     $$\mathrm{\Delta }{G}_{\text{total K}}=2\ast \frac{2537.2117805658827J}{mol}=\frac{5074.423561131765J}{mol}$$
     $$\mathrm{\Delta }{G}_{\text{total}}=\frac{38967.56170776904J}{mol}+\frac{5074.423561131765J}{mol}=\frac{44041.985268900804J}{mol}$$

   • determine whether ATP hydrolysis into ADP and Pi by the pump can drive this flow

     • ΔG for ATP hydrolysis (cellular conditions) is around –50,000 J/mol

     • One ATP molecule provides sufficient energy to drive the Na⁺/K⁺ pump

   • determine the energy needed if the stoichiometry is 2Na+ : 2K+

     $$\mathrm{\Delta }{G}_{\text{total}}=(2\ast \frac{12989.187235923013J}{mol})+(2\ast \frac{2537.2117805658827J}{mol})=\frac{31052.798032977793J}{mol}$$

     • Energy requirement decreases , and ATP hydrolysis still provides sufficient energy.

4. Determine the numerical value for the ratio $g_a^{Na}/g_b^K$$g_a^{Na} / g_b^{K}$ during steady-state Na+ absorption ( assuming a pump stoichiometry of 3Na+ : 2K+ )

   • At steady state:

     • the net current is zero

     • the current carried by Na⁺ entering the cell equals the current carried by K⁺ leaving the cell

     • adjusted for the pump stoichiometry

   $$\text{Ohm’s Law}:V=I\ast R$$

   • we can replace resistance $\left(R\right)$$\left(\ R\ \right)$ with conductance $\left(g\right)$$\left(\ g \ \right)$

   $$R=\frac{1}{g}$$
   $$\text{Ohm’s Law}:V=I\ast \frac{1}{g}$$

   • now , rewrite it , in terms of current $\left(I\right)$$\left(\ I \ \right)$

   $$\text{Ohm’s Law}=I=g\ast \mathrm{\Delta }V$$

   • ok , so to find this ratio of conductance values , we set up 2 Ohm's law equations , one for sodium , and one for potassium.

   • $V$$V$ , or $\mathrm{\Delta }V$$\Delta V$ , we are going to replace with the driving force. the driving force outputs a voltage anyways.

    

   $$N{a}^{+}\text{Current}\left(I_{Na}\right)=g_a^{Na}\ast (V_a-E_{Na})$$
   $$K^{+}\text{Current}\left(I_K\right)=g_b^K\ast (V_b-E_K)$$

   • so far we haven't done anything. we just wrote 2 Ohm's law equations

   ---

   • lets solve for both of the driving force parts

   $$(V_a-E_{Na})=(-25mV)-\left(69.68208013409848\right)=-94.68208013409848mV$$
   $$(V_b-E_K)=(-65mV)-(-91.37272471682026mV)=26.372724716820258mV$$

   ---

   • ok , now they gave us a ratio to find , $g_a^{Na}/g_b^K$$g_a^{Na} / g_b^{K}$ , so lets make our 2 Ohm's law equations match this

   $$\frac{I_{Na}}{I_K}=\frac{g_a^{Na}\ast (V_a-E_{Na})}{g_b^K\ast (V_b-E_K)}$$

   • we are going to treat the ions going through the pump as a current. so sodium current = -3 , and potassium = 2

   $$\frac{-3}{2}=\frac{g_a^{Na}\ast ((-25mV)-\left(69.68208013409848\right))}{g_b^K\ast ((-65mV)-(-91.37272471682026mV))}$$

   • simplifying

   $$-\frac{3}{2}=\frac{g_a^{Na}\ast (-94.68208013409848mV)}{g_b^K\ast \left(26.372724716820258mV\right)}$$

   • re-arranging for our goal ratio :

   $$\frac{g_a^{Na}}{g_b^K}=-\frac{3}{2}\ast \frac{26.372724716820258}{-94.68208013409848}=0.4178096533071807$$

5. Determine the direction for net flow of Cl- through the paracellular pathway.

   • Negative Transepithelial Potential ( Vₜₑ = –40 mV ) : Lumen is negative relative to the interstitium.

   • Cl⁻ (negative ion): Will be repelled by the negative lumen, moving from lumen to interstitium through the paracellular pathway.

   • Determine the electrochemical driving force for this flow.

     $$E_{Cl}=\frac{60}{-1}\ast lo{g}_{10}\left(\frac{116}{116}\right)=0mV$$

     • Driving Force : $\mathrm{\Delta }{V}_{Cl}=\left(V_{te}\right)-\left(E_{Cl}\right)=(-40mV)-\left(0mV\right)=-40mV$$\Delta V_{Cl} = \left(\ V_{te} \ \right) - \left(\ E_{Cl} \ \right) = \left(\ -40\ mV \ \right) - \left(\ 0\ mV \ \right) = -40\ mV$

     • Driving Force = negative

       • therefore think of the inside as being negative

       • chloride is negatively charged

         • therefore , it will want to leave the cell

   • Determine the luminal Cl- concentration at which net paracellular Cl- flow stops ( assuming constant interstitial concentration )

     • At equilibrium , net Cl- flow stops when :

     $$V_{te}=E_{Cl}$$
     $$E_{Cl}=-40mV$$

     • Using the Nernst equation :

     $$-40mV=\frac{60mV}{-1}\ast lo{g}_{10}\left(\frac{116}{[C{l}^{-}{]}_{\text{lumen}}}\right)$$

     • Divide both sides by -60 mV :

     $$\frac{40}{60}=lo{g}_{10}\left(\frac{116}{[C{l}^{-}{]}_{\text{lumen}}}\right)$$

     • Solve for $[C{l}^{-}{]}_{\text{lumen}}$$[\ Cl^-\ ]_{\text{lumen}}$ :

     $${10}^{\frac{40}{60}}=\frac{116}{[C{l}^{-}{]}_{\text{lumen}}}$$
     $$[C{l}^{-}{]}_{\text{lumen}}=\frac{116}{{10}^{\frac{40}{60}}}=24.991442404369852mM$$

     • Conclusion :

       • Net Cl- Flow Direction = from lumen to interstitium

       • Electrochemical Driving Force = -40 mV

       • Luminal [ Cl- ] at Equilibrium = Approximately 25 mM

6. Continued electrogenic Na+ absorption will drive salt flow out of the lumen such that luminal Na+ and Cl- concentrations could drop by 5 mM. Determine the hydrostatic pressure necessary to oppose and thereby stop the resulting osmotic flow of water.

   $$\mathrm{\Delta }\mathrm{\Pi }=n\ast R\ast T\ast \mathrm{\Delta }C$$
   $$\mathrm{\Delta }\mathrm{\Pi }=2\ast \frac{0.0821L\cdot atm}{mol\cdot K^{\circ }}\ast (29C^{\circ }+273.15K^{\circ })\ast \frac{0.005mol}{L}=0.24560215000000002atm\ast \frac{760mmHg}{1atm}=186.657634mmHg$$

    

   • Hydrostatic Pressure Needed : Approximately 186 mmHg to oppose and stop the osmotic flow of water resulting from a 5 mM decrease in luminal Na⁺ and Cl⁻ concentrations.

• Transepithelial secretion of Cl- is electrogenic and occurs at several epithelial sites , including salivary glands , pancreatic acini , and intestine.

• This electrogenic Cl- secretion requires Na+ / K+ pumps , K+ channels , and Na+ \ K+ \ 2Cl- cotransporters in the basolateral membrane

  • together with apical membrane Cl- channels.

• Draw a diagram for an epithelial cell containing these transport components.

  • Basolateral Membrane (facing interstitium):

    • Na⁺/K⁺ ATPase Pump: Actively transports 3 Na⁺ ions out of the cell and 2 K⁺ ions into the cell.

    • K⁺ Channels: Allow passive diffusion of K⁺ ions out of the cell.

    • Na⁺-K⁺-2Cl⁻ Cotransporter (NKCC1): Co-transports 1 Na⁺, 1 K⁺, and 2 Cl⁻ ions into the cell.

  • Apical Membrane (facing lumen):

    • Cl⁻ Channels (e.g., CFTR): Allow Cl⁻ ions to exit the cell into the lumen.

• Initially , the lumen is assumed to have the same composition as the interstitial space.

1. Stimulation of Cl- secretion produces a depolarization of $V_a$$V_a$ from -70 mV to -34 mV within ~30 sec. By 3 min after stimulation, Cl- secretion is maximal and $V_a$$V_a$ stabilizes at -45 mV. ( Draw a graph of the time course , $V_a$$V_a$ versus time )

   • Time (x-axis): From 0 to 3 minutes.

   • $V_a$$V_a$ (y-axis): Membrane potential ranging from -70 mV to -34 mV.

   • Description: Starting at -70 mV at time 0 , $V_a$$V_a$ depolarizes to -34 mV within 30 seconds.

     • It then hyperpolarizes slightly to stabilize at -45 mV by 3 minutes.

   • Determine the electrochemical driving force acting on Cl- flow through the apical membrane Cl- conductance ( $g_a^{Cl}$$g_a^{Cl}$ ) at the time of peak depolarization.

     • @ Peak Depolarization : $V_a=-34mV$$V_a = -34\ mV$

     $$E_{Cl}=\frac{60}{-1}\ast lo{g}_{10}\left(\frac{116}{39}\right)=-28.403602932025155mV$$
     $$\text{Driving Force}=(-34mV)-(-28.403602932025155mV)=-5.596397067974845mV$$

   • If $V_a$$V_a$ depolarizes to -29 mV , determine the electrochemical driving force for this conductive Cl- flow.

     $$\text{Driving Force}=(-29mV)-(-28.403602932025155mV)=-0.5963970679748449mV$$

   • Intracellular Cl- concentration decreases ~10% by 1 min after stimulation and returns to the initial value during steady-state secretion. Determine the numerical value of $E_{Cl}^a$$E_{Cl}^a$ a at 1 min after stimulation.

     $$[C{l}^{-}{]}_{\text{inside}}=39mM\ast (100\mathrm{\%}-10\mathrm{\%})=35.1mM$$
     $$E_{Cl}=\frac{60}{-1}\ast lo{g}_{10}\left(\frac{116}{35.1}\right)=-31.149052365665664mV$$

   • Speculate on the most likely cause for the decrease and return of Cl- concentration during the onset of the secretory state.

     • Decrease in Intracellular Cl⁻ :

       • Rapid efflux of Cl⁻ through apical Cl⁻ channels exceeds the rate of Cl⁻ entry via basolateral cotransporters.

     • Return to Initial Value :

       • Upregulation or increased activity of Na⁺-K⁺-2Cl⁻ cotransporters restores intracellular Cl⁻ levels as Cl⁻ influx balances efflux.

     • Answer = The initial decrease is due to Cl⁻ efflux exceeding influx; the return is due to increased Cl⁻ uptake restoring balance.

   • Determine the electrochemical driving force for conductive Cl- flow through $g_a^{Cl}$$g_a^{Cl}$ during steady-state Cl- secretion.

     • At steady state $(V_a=-45mV)$$\left(\ V_a = -45\ mV \ \right)$

     $$\text{Driving Force}=(-45mV)-(-28.403602932025155mV)=-16.596397067974845mV$$

2. During steady state secretion , $V_b$$V_b$ is -65 mV

   • Determine the electrochemical driving force for conductive flow of K+ through $g_b^K$$g_b^{K}$

     $$E_K=\frac{60}{+1}\ast lo{g}_{10}\left(\frac{4.5}{150}\right)=-91.37272471682026mV$$
     $$\text{Driving Force}=(-65mV)-(-91.37272471682026mV)=26.372724716820258mV$$

   • Determine the electrochemical driving force for Na+ \ K+ \ 2Cl- cotransporters ( $\frac{\mathrm{\Delta }{\mu }_{NaK2CL}}{F}$$\frac{\Delta \mu_{NaK2CL}}{F}$ ) in the basolateral membrane

     $$\frac{\mathrm{\Delta }{\mu }_{NaK2CL}}{F}=V_b+(\left(\frac{R\ast T}{F}\right)\ast ln\left(\frac{[N{a}^{+}{]}_{\text{i}}\ast [K^{+}{]}_{\text{i}}\ast [C{l}^{-}{]}_{\text{i}}^2}{[N{a}^{+}{]}_{\text{o}}\ast [K^{+}{]}_{\text{o}}\ast [C{l}^{-}{]}_{\text{o}}^2}\right))$$
     $$\frac{\mathrm{\Delta }{\mu }_{NaK2CL}}{F}=(-0.065V)+(\left(\frac{\frac{8.314J}{mol\cdot K^{\circ }}\ast (29C^{\circ }+273.15K^{\circ })}{\frac{96485J}{Volts\cdot mol}}\right)\ast ln\left(\frac{10\ast 50\ast {\left(39\right)}^2}{145\ast 4.5\ast {\left(116\right)}^2}\right))=-0.10008724244812786V$$

   • Determine the driving force for Na+ \ Cl- cotransporters.

     $$\frac{\mathrm{\Delta }{\mu }_{NaCl}}{F}=(-0.065V)+(\left(\frac{\frac{8.314J}{mol\cdot K^{\circ }}\ast (29C^{\circ }+273.15K^{\circ })}{\frac{96485J}{Volts\cdot mol}}\right)\ast ln\left(\frac{10\ast 39}{145\ast 116}\right))=-0.16300379128411935V$$

   • Determine the intracellular Na+ concentration at which net flow stops for each type of cotransporter ( assuming that the other concentrations were unchanged ).

     $$\text{Let}\frac{\mathrm{\Delta }{\mu }_{NaK2Cl}}{F}=0$$
     $$0=V_b+(\left(\frac{\frac{8.314J}{mol\cdot K^{\circ }}\ast (29C^{\circ }+273.15K^{\circ })}{\frac{96485J}{Volts\cdot mol}}\right)\ast ln\left(\frac{[N{a}^{+}{]}_{\text{i}}\ast [K^{+}{]}_{\text{i}}\ast [C{l}^{-}{]}_{\text{i}}^2}{[N{a}^{+}{]}_{\text{o}}\ast [K^{+}{]}_{\text{o}}\ast [C{l}^{-}{]}_{\text{o}}^2}\right))$$

     • Solve for $[N{a}^{+}{]}_{\text{inside}}$$[\ Na^+\ ]_{\text{inside}}$ :

     $$ln\left(\frac{[N{a}^{+}{]}_{\text{inside}}\ast }{[N{a}^{+}{]}_{\text{outside}}}\right)=-(ln\left(\frac{[K^{+}{]}_{\text{i}}\ast [C{l}^{-}{]}_{\text{i}}^2}{[K^{+}{]}_{\text{o}}\ast [C{l}^{-}{]}_{\text{o}}^2}\right)+\frac{V_b\ast F}{R\ast T})$$
     $$ln\left(\frac{[N{a}^{+}{]}_{\text{inside}}\ast }{145}\right)=-(ln\left(\frac{150\ast {\left(39\right)}^2}{4.5\ast {\left(116\right)}^2}\right)+\frac{-0.065V\ast \frac{96485J}{Volts\cdot mol}}{\frac{8.314J}{mol\cdot K^{\circ }}\ast (29C^{\circ }+273.15K^{\circ })})$$
     $$\frac{[N{a}^{+}{]}_{\text{inside}}\ast }{145}=e^{(-(ln\left(\frac{150\ast {\left(39\right)}^2}{4.5\ast {\left(116\right)}^2}\right)+\frac{-0.065V\ast \frac{96485J}{Volts\cdot mol}}{\frac{8.314J}{mol\cdot K^{\circ }}\ast (29C^{\circ }+273.15K^{\circ })}))}$$

     145 * math.e**( -( math.log( ( 150 * ( 39**2 ) ) / ( 4.5 * ( 116**2 ) ) ) + ( ( -0.065 * 96485 ) / ( 8.314 * ( 29 + 273.15 ) ) ) ) )
     

     $$[N{a}^{+}{]}_{\text{inside}}=145\ast e^{(-(ln\left(\frac{150\ast {\left(39\right)}^2}{4.5\ast {\left(116\right)}^2}\right)+\frac{-0.065V\ast \frac{96485J}{Volts\cdot mol}}{\frac{8.314J}{mol\cdot K^{\circ }}\ast (29C^{\circ }+273.15K^{\circ })}))}=467.2126424450802mM$$

     ---

     $$\text{Let}\frac{\mathrm{\Delta }{\mu }_{NaCl}}{F}=0$$
     $$[N{a}^{+}{]}_{\text{inside}}=145\ast e^{(-(ln\left(\frac{39}{116}\right)+\frac{-0.065V\ast \frac{96485J}{Volts\cdot mol}}{\frac{8.314J}{mol\cdot K^{\circ }}\ast (29C^{\circ }+273.15K^{\circ })}))}=5236.003751539691mM$$

   • Determine the numerical value for the ratio $g_a^{Cl}/g_b^K$$g_a^{Cl} / g_b^{K}$ during steady-state Cl- secretion

     • At steady state , current = 0

     $$I_{Cl}+I_K=0$$
     $$\therefore ,I_{Cl}=-I_K$$

     ---

     $$I_{Cl}=g_a^{Cl}\ast (V_a-E_{Cl}^a)$$
     $$I_{Cl}=g_a^{Cl}\ast ((-45mV)-(-31.149052365665664mV))=g_a^{Cl}\ast -13.850947634334336$$
     $$I_K=g_b^K\ast (V_b-E_K^b)$$
     $$I_K=g_b^K\ast ((-65mV)-(-91.37272471682026mVmV))=g_b^K\ast 26.372724716820258mV$$

     ---

     $$g_a^{Cl}\ast -13.850947634334336=-g_b^K\ast 26.372724716820258mV$$
     $$\frac{g_a^{Cl}}{g_b^K}=\frac{26.372724716820258mV}{13.850947634334336mV}=1.9040375729561199$$

   • Determine the conductance for these Cl- channels compared with the conductance for these Na+ \ K+ \ 2Cl- cotransporters during steady-state Cl- secretion.

     • Na⁺-K⁺-2Cl⁻ Cotransporter :

       • Electrically neutral ( no net charge movement ).

       • Does not contribute to membrane conductance in terms of ionic current.

     • Comparison :

       • The apical Cl⁻ channel conductance $\left(g_a^{Cl}\right)$$\left(\ g_a^{Cl} \ \right)$ is approximately 1.9 times the basolateral K⁺ channel conductance $g_b^K$$g_b^{K}$

       • The cotransporter's activity affects ion concentrations but not membrane conductance.

     • Answer: The Cl⁻ channel conductance is significantly higher compared to the K⁺ channel, while the cotransporter does not contribute to conductance.

• Transepithelial absorption of glucose occurs in the small intestine and is electrogenic , making the lumen negative relative to the interstitium.

• Glucose absorption requires Na+ / K+ pumps , K+ channels , and glucose transporters in the basolateral membrane together with apical membrane Na+ \ glucose cotransporters.

• Draw a diagram for an epithelial cell containing these transport components.

  • asdf

• Initially , the lumen is assumed to have the same composition as the interstitial space ,

  • except with 25 mM glucose; the interstitium has 6 mM glucose.

• During glucose absorption , $V_b=-65mV$$V_b = -65\ mV$ and $V_a=-55mV$$V_a = -55\ mV$

1. Determine the electrochemical driving force for glucose flow via Na+ \ glucose cotransporters ( $\frac{\mathrm{\Delta }{\mu }_{SGLT}}{F}$$\frac{\Delta \mu_{SGLT}}{F}$ ) , if the stoichiometry is 2Na+ : 1glucose and the intracellular glucose concentration is 10 mM.

   • asdf

   • If the stoichiometry is 1Na+ : 1glucose , determine the electrochemical driving force for apical membrane glucose flow.

     • asdf

   • Determine the number of glucose molecules absorbed for each ATP hydrolyzed by the 3Na+ / 2K+ exchange pumps.

     • asdf

2. Determine the electrochemical driving force for glucose flow via the basolateral membrane glucose transporters ( $\frac{\mathrm{\Delta }{\mu }_{GLUT}}{F}$$\frac{\Delta \mu_{GLUT}}{F}$ )

   • asdf

3. Determine the conductance of the basolateral membrane glucose transporters compared with the conductance of the apical Na+ \ glucose cotransporters, during steady-state glucose absorption.

   • asdf

4. Determine the intracellular glucose concentration at which apical glucose flow stops , if basolateral glucose flow were inhibited completely ( other features remaining the same ).

   • asdf

5. Luminal glucose concentration decreases during continual absorption. ( assume a luminal glucose concentration of 0.1 mM )

   • Determine the electrochemical driving force for apical glucose flow , with each type of cotransporter stoichiometry.

     • asdf

   • Determine the conductance of the basolateral membrane glucose transporters compared with the conductance of the Na+ \ glucose cotransporters, during steady-state glucose absorption.

     • asdf

6. Determine the luminal glucose concentration at which net glucose absorption stops ( assuming negligible paracellular glucose permeability )

   • asdf

• An apical membrane H+ / K+ exchange pump , drives acid secretion in the parietal cells of the stomach.

• In addition , acid secretion requires Cl- / HCO3- exchangers in the basolateral membrane together with apical membrane K+ channels and Cl- channels.

• Carbonic anhydrase speeds the interconversion of CO2 and HCO3- and is present at intracellular and interstitial sites.

• Draw a cell diagram that shows the route of a H+ moving from the interstitial space to the lumen.

  

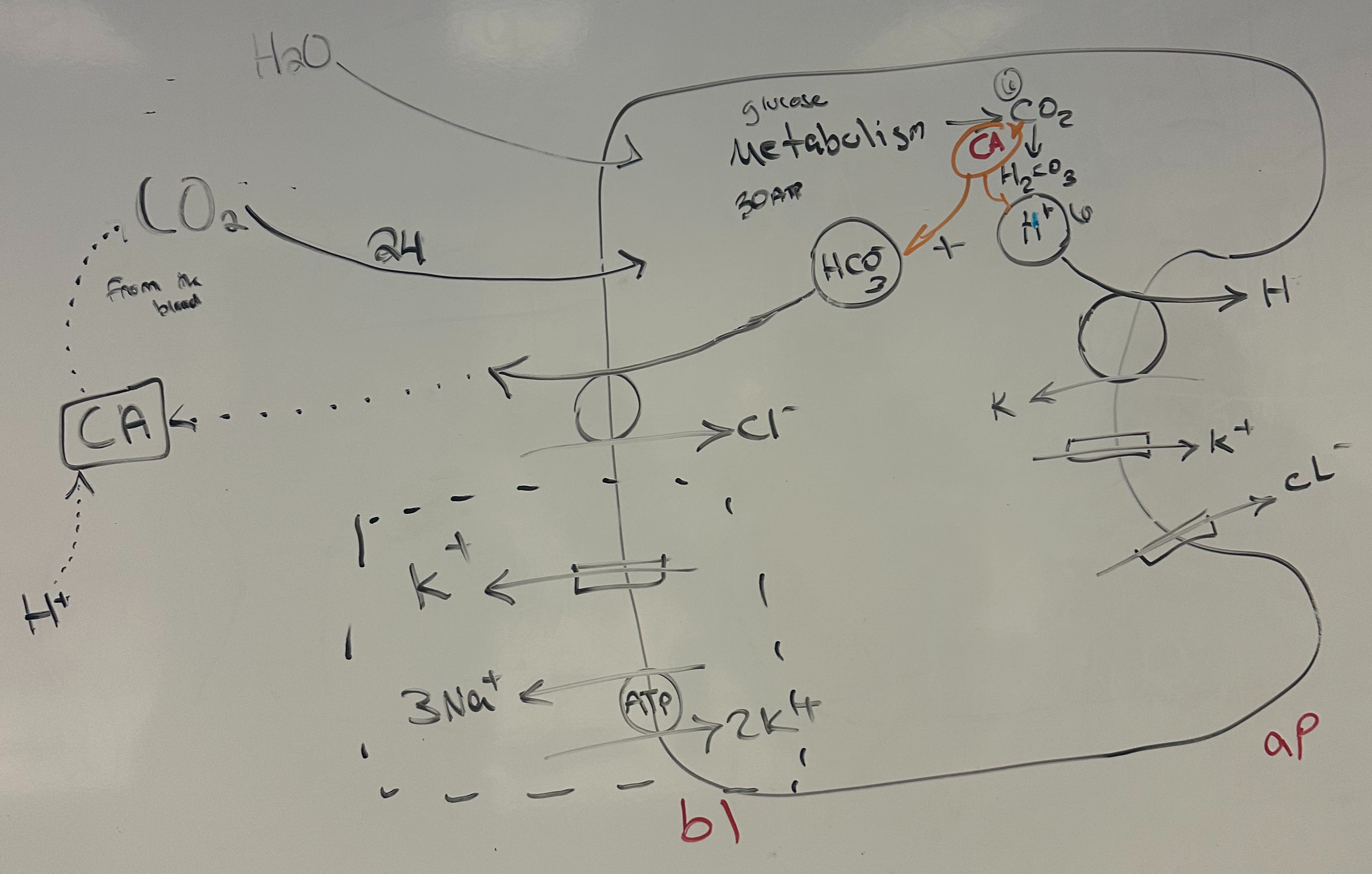
• Estimate what fraction of the CO2 needed for acid secretion might come from parietal cell metabolism.

  • H⁺/K⁺ ATPase pump on the apical membrane secretes H⁺ into the stomach lumen in exchange for K⁺.

  • Cl⁻/HCO₃⁻ exchanger on the basolateral membrane exchanges Cl⁻ into the cell and HCO₃⁻ out into the blood.

  • Cl⁻ and K⁺ channels on the apical membrane allow Cl⁻ and K⁺ to flow into the stomach lumen.

  • Carbonic anhydrase converts CO₂ and H₂O into HCO₃⁻ and H⁺ inside the cell.

   

  CO₂ Estimation:

  A significant fraction of the CO₂ used for H⁺ production likely comes from cellular metabolism. The parietal cells are metabolically active, and CO₂ is produced as a byproduct of cellular respiration. Some CO₂ is also supplied from the blood as it diffuses into the parietal cells from the interstitial space.

  If you want to estimate the fraction, the proportion depends on the balance between:

  1. Metabolic CO₂ production within the parietal cell (from processes like the citric acid cycle).

  2. CO₂ supplied from blood plasma as dissolved CO₂ in circulation.

  Given that cells use internal CO₂ extensively in metabolic pathways, it’s plausible that a majority (~60–70%) of the CO₂ used comes from metabolism, with the remaining supplied via the bloodstream. This is a rough estimate and could vary depending on the specific conditions in the stomach and blood supply.

• Absorption of Na+ and Cl- in the ileal portion of the small intestine proceeds via a cellular pathway.

• The mechanism of absorption requires Na+ / H+ exchangers and Cl- / HCO3- exchangers in the apical membrane together with basolateral membrane Na+ / K+ pumps , K+ channels , and Cl- channels.

• In addition , these epithelial cells contain soluble carbonic anhydrase , which interconverts CO2 and HCO3- , and membrane bound carbonic anhydrase found on the luminal side of the apical membrane.

• Draw a cell diagram that includes the movements of HCO3- and H+ through the apical membrane and the interactions with carbonic anhydrase.

  

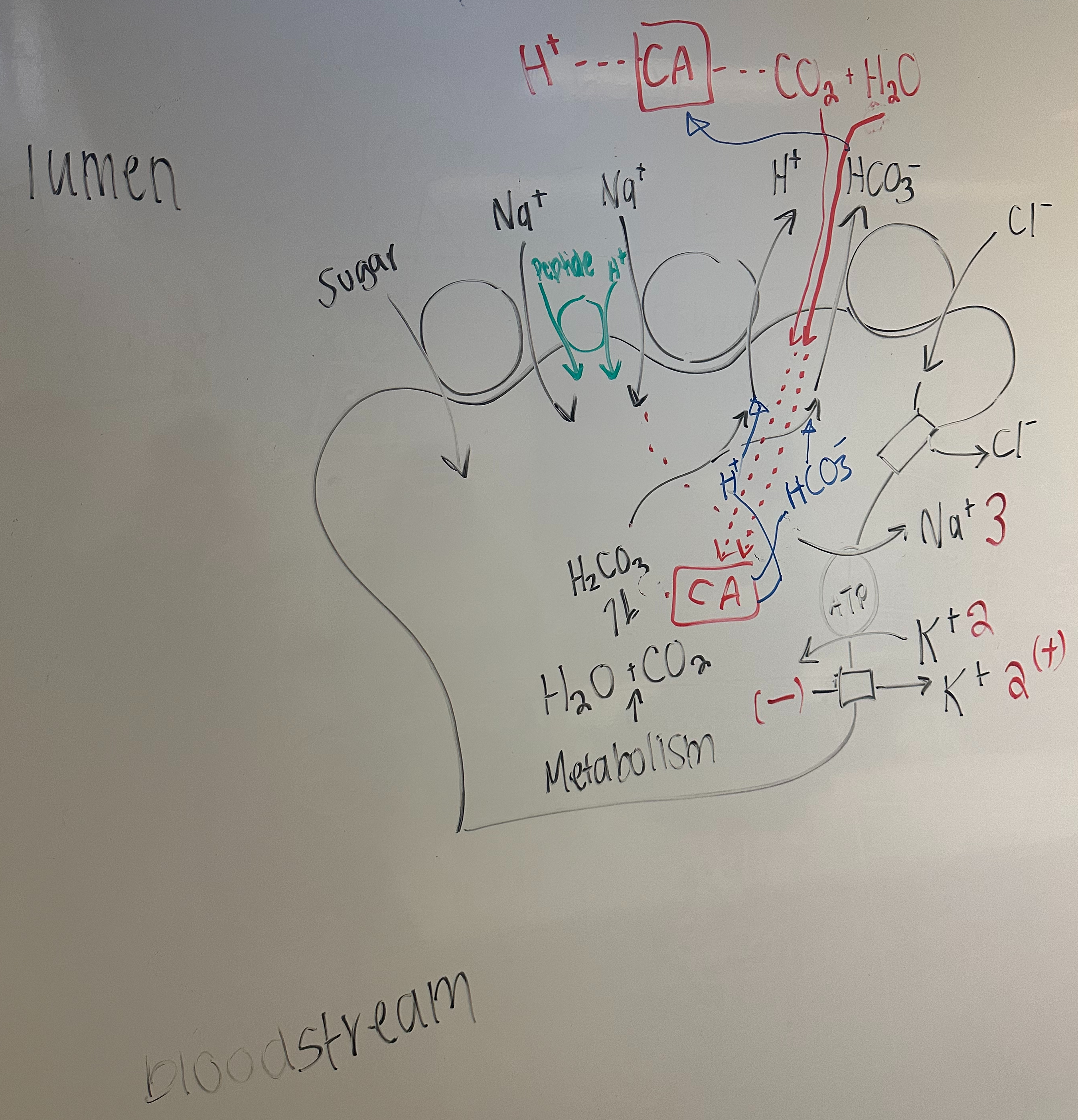
• Predict what would happen to luminal composition [ ion concentrations , pH, volume ] for individuals with a congenital defect making the apical Na+ / H+ exchangers inoperable

  • Ion Concentrations:

    • Decreased Na⁺ Absorption:

      • Mechanism: The Na⁺/H⁺ exchanger is crucial for absorbing Na⁺ from the lumen into the cell.

      • Outcome: Na⁺ remains in the lumen, leading to increased luminal Na⁺ concentration.

    • Decreased H⁺ Secretion:

      • Mechanism: H⁺ is normally secreted into the lumen in exchange for Na⁺.

        • Outcome: H⁺ accumulates inside the cell, potentially affecting intracellular pH.

  • Luminal pH:

    • Increased pH (Alkalinity):

      • Mechanism: Reduced secretion of H⁺ into the lumen means fewer protons are available to acidify the lumen.

      • Outcome: The luminal environment becomes less acidic (more alkaline).

  • Luminal Volume:

    • Increased Volume (Potential Diarrhea):

      • Mechanism: Unabsorbed Na⁺ in the lumen increases osmolarity, drawing water into the lumen or preventing its absorption.

      • Outcome: Increased luminal volume can lead to diarrhea due to excess water in the intestinal contents.

  • Additional Considerations:

    • Intracellular Acidification:

      • Accumulation of H⁺ inside the cell may lead to decreased intracellular pH, potentially disrupting cellular functions.

      • Secondary Effects on Cl⁻ Absorption:

        • Reduced Na⁺ absorption can indirectly affect Cl⁻ absorption, as the electrochemical gradients are altered.

• Predict what would happen to luminal composition [ ion concentrations , pH, volume ] for individuals with a congenital defect making the apical Cl- / HCO3- exchangers inoperable

  • Ion Concentrations:

    • Decreased Cl⁻ Absorption:

      • Mechanism: The Cl⁻/HCO₃⁻ exchanger is essential for absorbing Cl⁻ from the lumen into the cell.

      • Outcome: Cl⁻ remains in the lumen, leading to increased luminal Cl⁻ concentration.

    • Decreased HCO₃⁻ Secretion:

      • Mechanism: HCO₃⁻ is normally secreted into the lumen in exchange for Cl⁻.

      • Outcome: HCO₃⁻ accumulates inside the cell, potentially leading to intracellular alkalosis.

  • Luminal pH:

    • Decreased pH (Acidity):

      • Mechanism: Reduced secretion of HCO₃⁻, a base, into the lumen results in less neutralization of luminal H⁺.

      • Outcome: The luminal environment becomes more acidic due to the continued secretion of H⁺ via Na⁺/H⁺ exchangers.

  • Luminal Volume:

    • Increased Volume (Potential Diarrhea):

      • Mechanism: Unabsorbed Cl⁻ in the lumen increases osmolarity, drawing water into the lumen or preventing its absorption.

      • Outcome: Increased luminal volume can lead to diarrhea due to excess water in the intestinal contents.

  • Additional Considerations:

    • Intracellular Alkalosis:

      • Accumulation of HCO₃⁻ inside the cell may raise intracellular pH, potentially affecting enzyme activities and cellular metabolism.

    • Impact on Na⁺ Absorption:

      • While Na⁺ absorption via the Na⁺/H⁺ exchanger may continue, the overall absorption efficiency is reduced due to the imbalance of other ions.