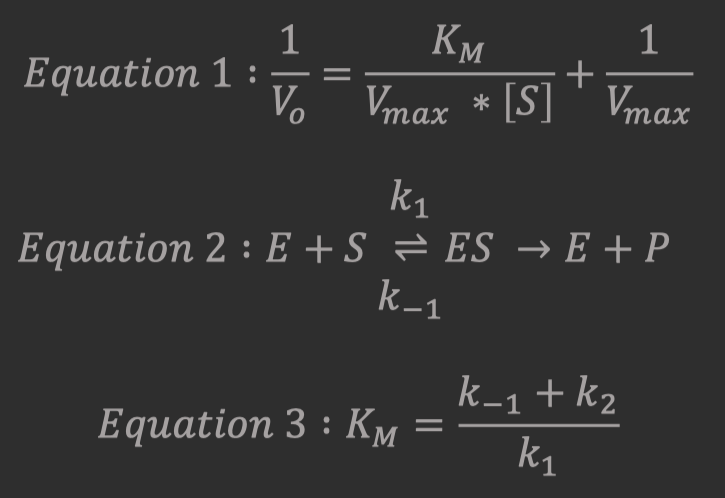Michaelis-Menton Equation

• The Michaelis-Menten equation describes the rate of an enzymatic reaction as a function of substrate concentration.
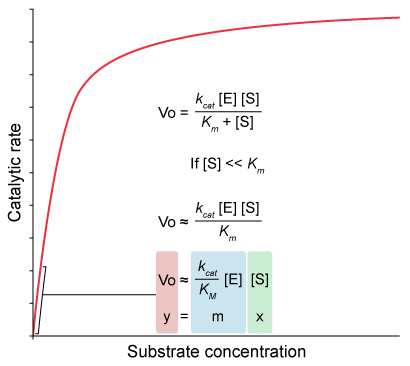
• It is written in the form :

$$V_0=\frac{V_{max}\ast [S]}{[K_m]+[S]}$$

• where :

  • $[S]$$[S]$ = substrate concentration

  • $V_0$$V_0$ = observed reaction rate at a given $[S]$$[S]$

  • $V_{max}$$V_{max}$ = maximum possible reaction rate

  • $[K_m]$$[K_m]$ :

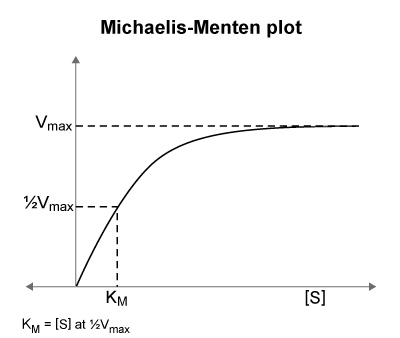
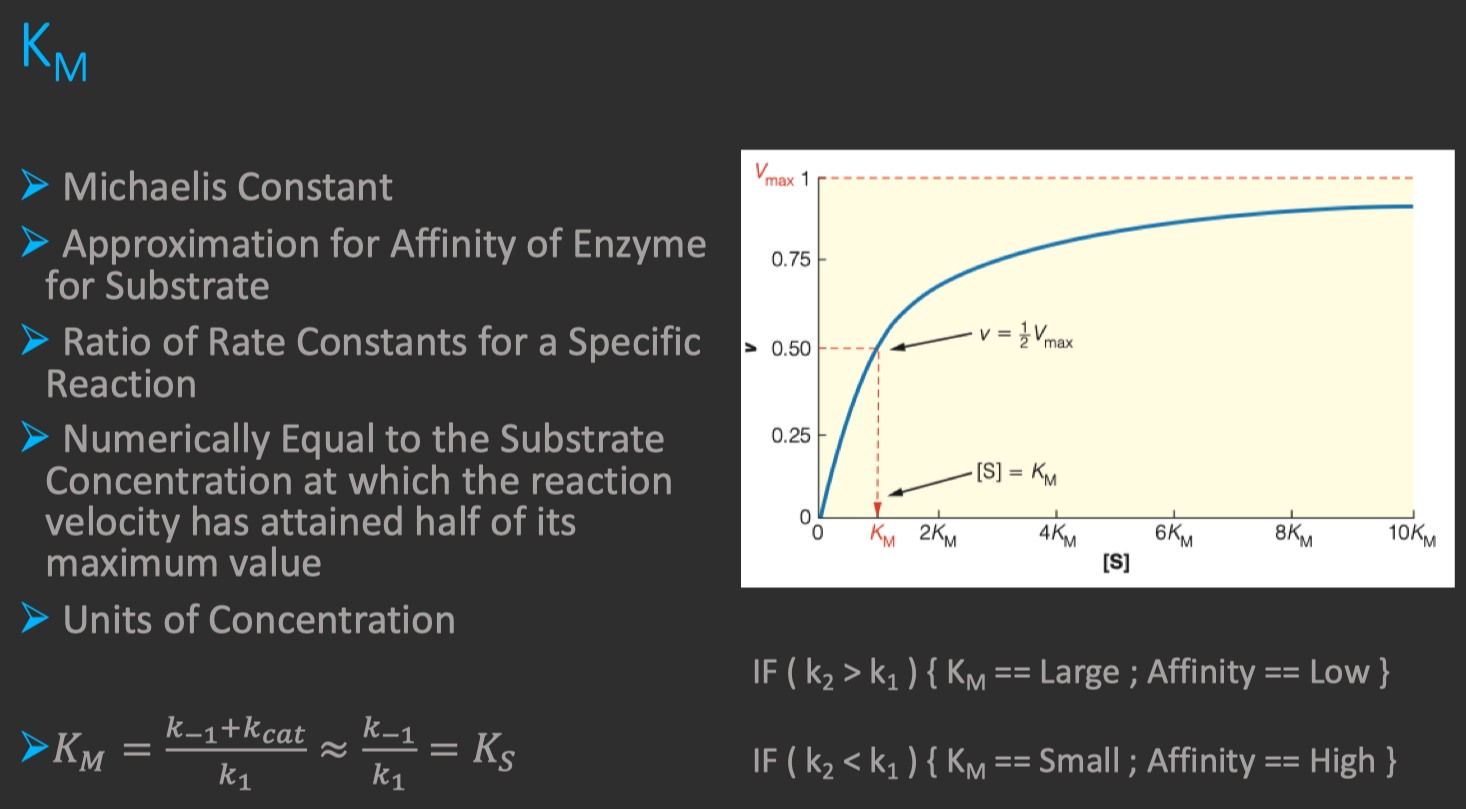
    • Michaelis constant

    • substrate concentration at which $\frac{V_{max}}{2}$$\frac{V_{max}}{2}$ is achieved

    • also a "measure" of the affinity of Enzyme for Substrate

    • $\propto$$\propto$ Binding Tightness of ES complex

      • smaller values of $K_m$$K_m$ mean the Enzyme is more tightly bound to the Substrate

$$E+S\stackrel{k_f}{\underset{k_r}{\stackrel{-\rightharpoonup }{\leftharpoondown -}}}ES\stackrel{k_{cat}}{⟶}E+P$$

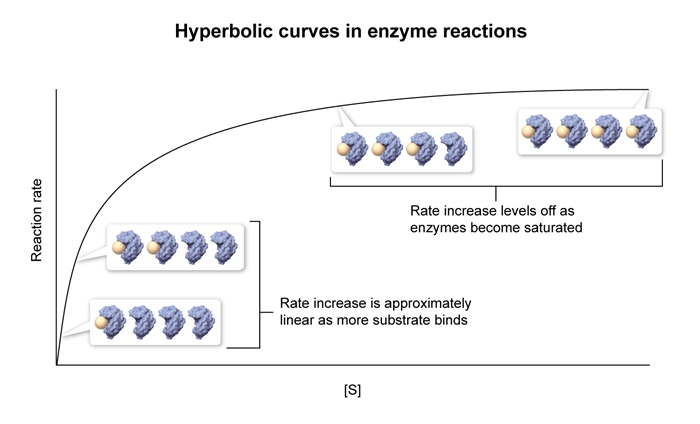
• As $[S]$$[S]$ increases , $V_0$$V_0$ increases hyperbolically , approaching a plateau at $V_{max}$$V_{max}$
• When $[S]$$[S]$ = $K_m$$K_m$ , the Michaelis-Menten equation can be rewritten as :

$$V_0=\frac{V_{max}\ast K_m}{K_m+K_m}=\frac{V_{max}\ast \cancel{K_m}}{2\ast \cancel{K_m}}=\frac{V_{max}}{2}$$

• Therefore , when $[S]$$[S]$ is equal to $K_m$$K_m$ , the reaction proceeds at $\frac{V_{max}}{2}$$\frac{V_{max}}{2}$

• The Michaelis-Menten equation describes the rate of an enzymatic reaction as a function of substrate concentration.
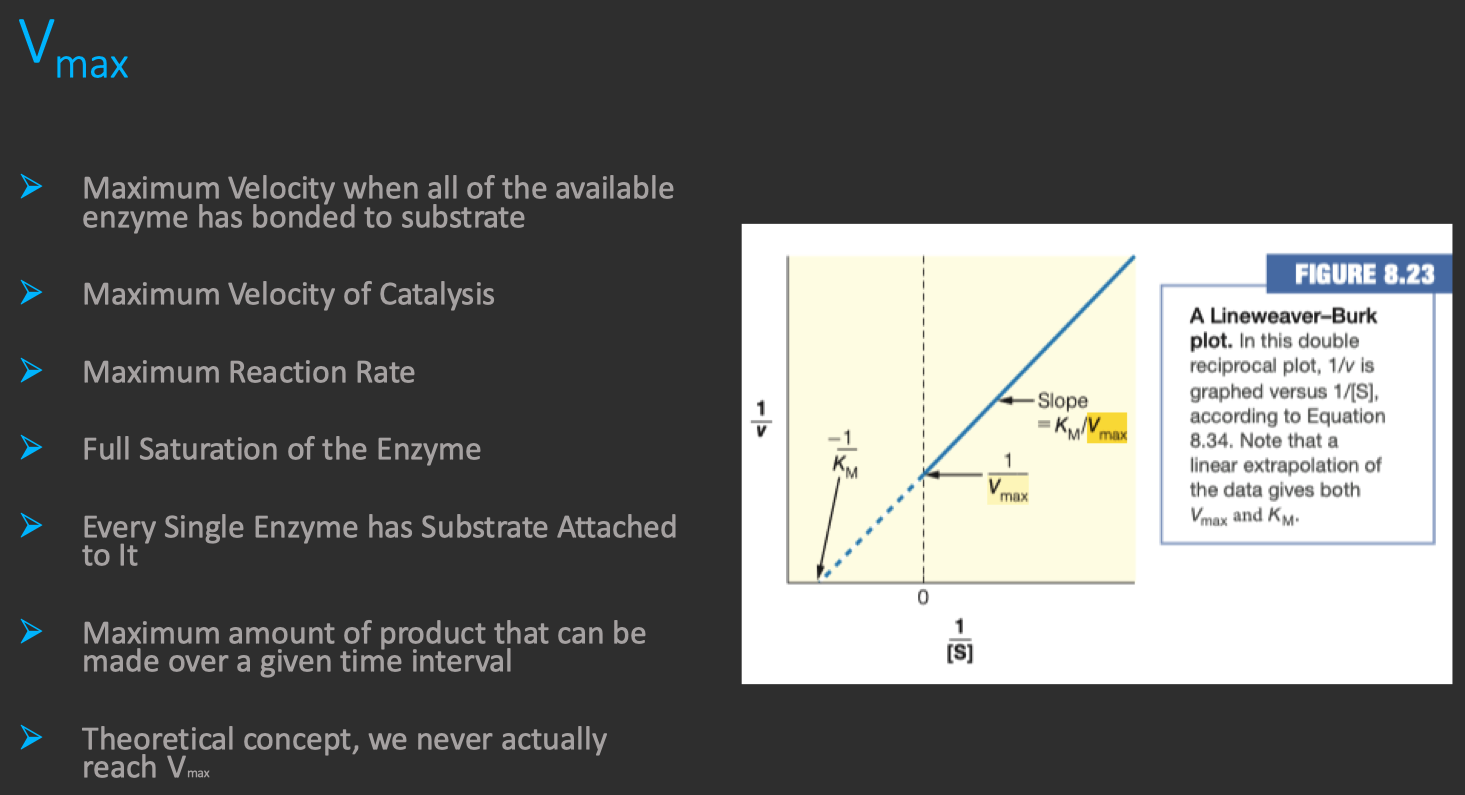
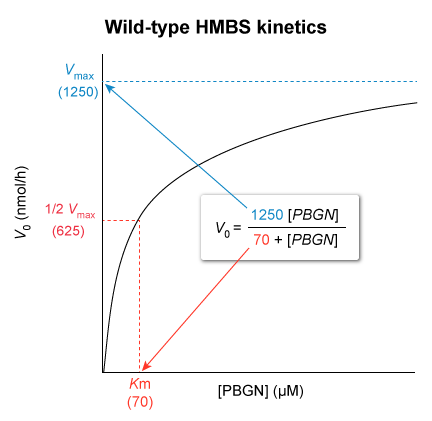
• The maximum reaction velocity $V_{max}$$V_{max}$ , found in the numerator of the equation , indicates the height of the plateau that the graph approaches.
• The $K_m$$K_m$ , found in the denominator , is the substrate concentration at which $\frac{V_{max}}{2}$$\frac{V_{max}}{2}$ is achieved.

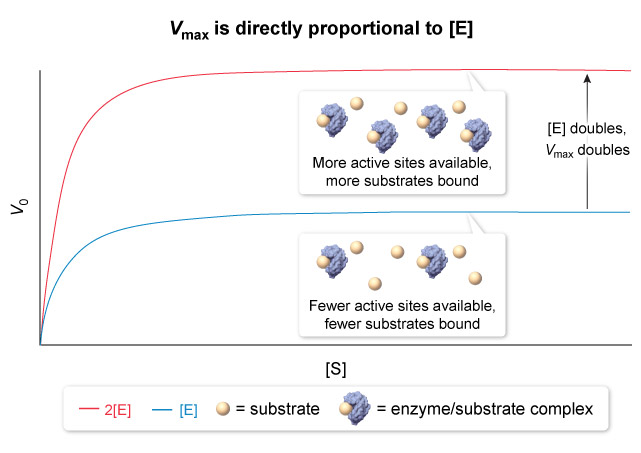
• $V_{max}$$V_{max}$ is achieved when $[S]$$[S]$ is high enough that all enzyme active sites are bound by substrate , a condition known as saturation.
• $V_{max}$$V_{max}$ is directly proportional to the concentration of enzyme in solution , expressed mathematically as :

$$V_{max}=k_{cat}\ast [E]$$

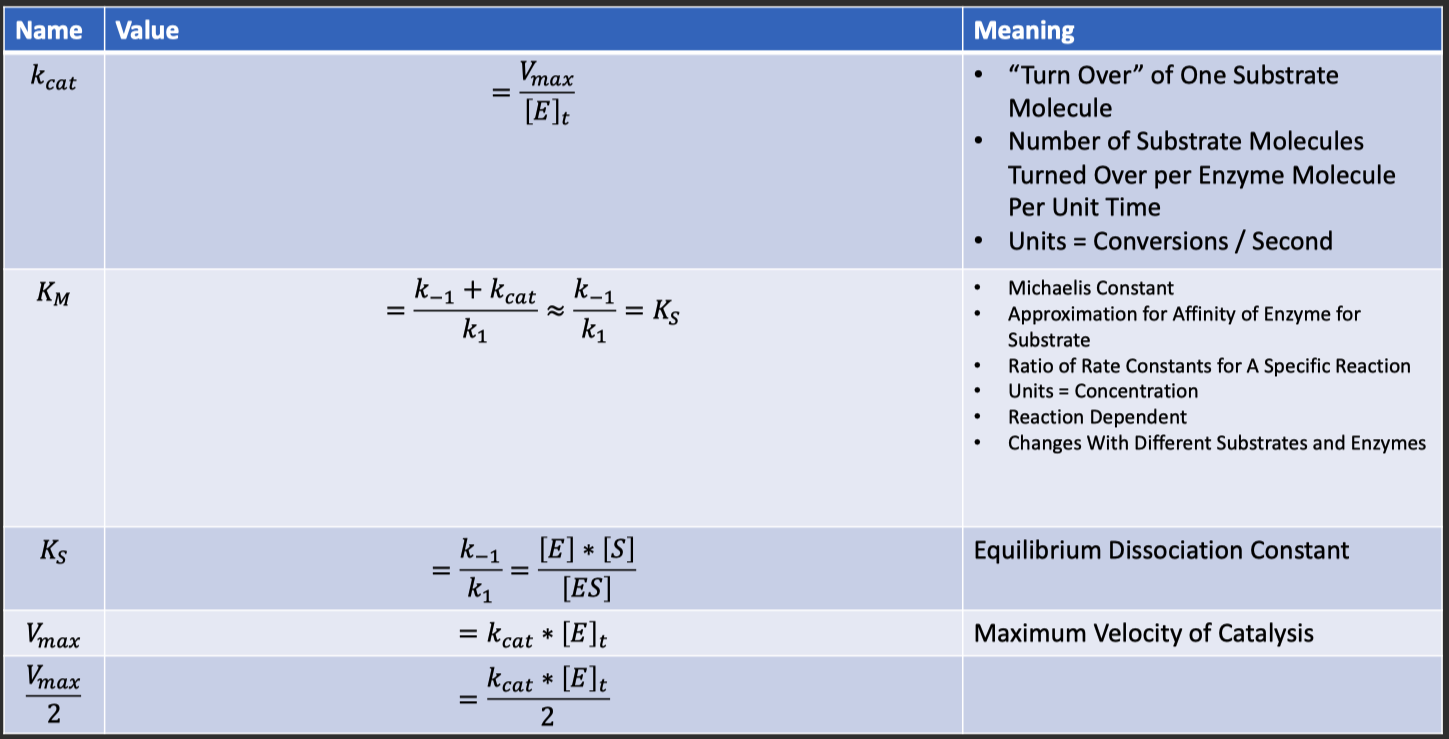
• Where $[E]$$[E]$ is the total enzyme concentration and $k_{cat}$$k_{cat}$ is the turnover number , or the number of reactions catalyzed per second of enzyme at saturation.
• At saturation , increasing $[S]$$[S]$ will not increase the reaction rate because $V_{max}$$V_{max}$ has already been achieved.
• Increasing the enzyme concentration , on the other hand , increases the number of active sites present in solution , and therefore increases $V_{max}$$V_{max}$

• The rate of an enymatic reaction is directly proportional to the concentration of enzyme present in the reaction.
• When the active sites on an enzyme are saturated , an increase in substrate concentration will NOT change the reaction rate but an increase in enzyme concentration will.

Experimentally Determining $V_{max}$$V_{max}$ and $K_m$$K_m$

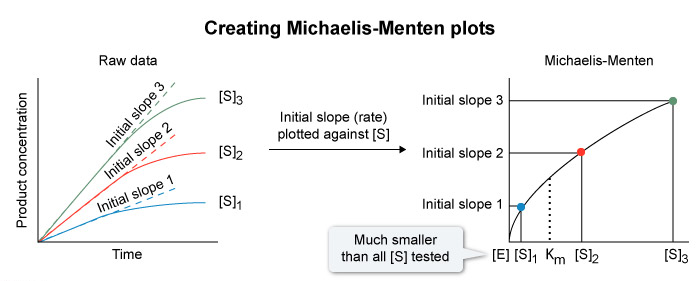
• Michaelis-Menten kinetics are determined by measuring the rate of product formation in the presence of varying concentrations of substrate.

• The reaction rate ( initial slope ) at each substrate concentration is than plotted as a single point , with concentration on the x-axis and rate on the y-axis , yielding a hyperbolic curve ( Michaelis-Menten plot ) described by the Michaelis-Menten equation

• The Michaelis-Menten equation relies on three assumptions :

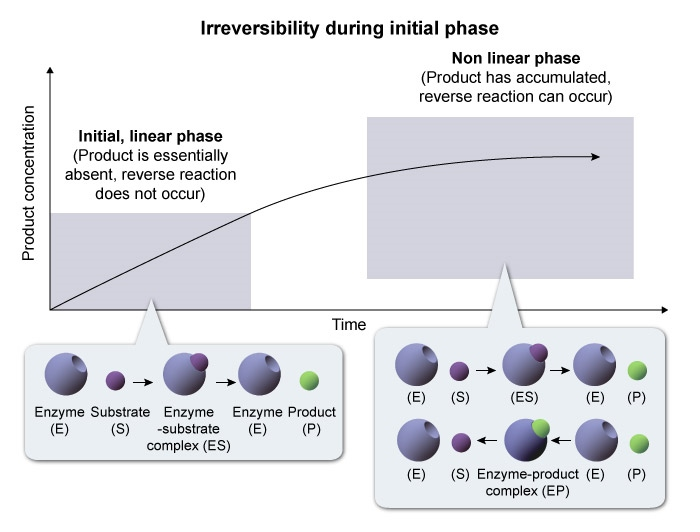
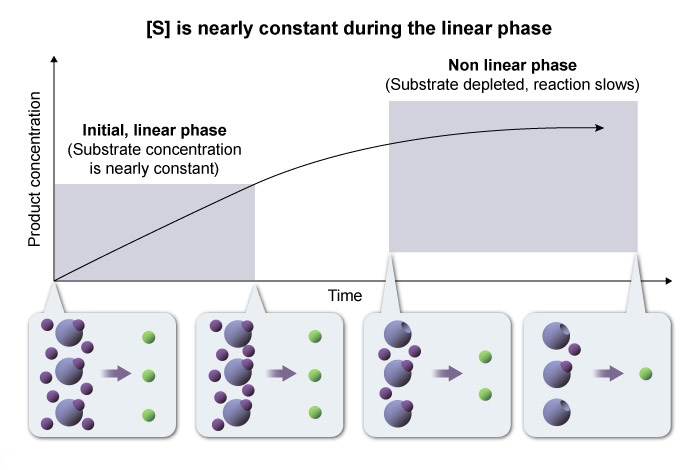
  • The free ligand approximation states that substrate concentration $[S]$$[S]$ is constant during the reaction.
  • This approximation is only true during the initial phase of the reaction , before a significant amount of substrate is converted to product.
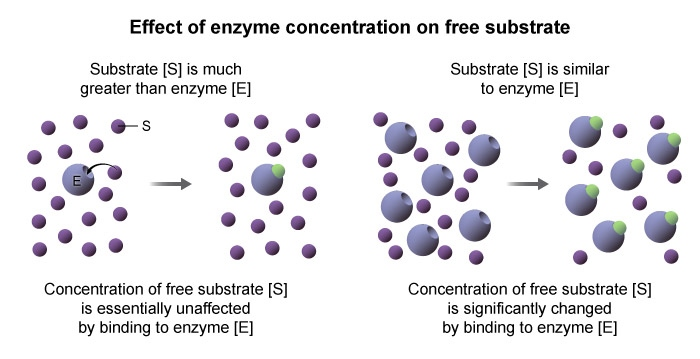
  • Substrate can also be depleted when it binds the enzyme to form the enzyme-substrate complex ( ES ).
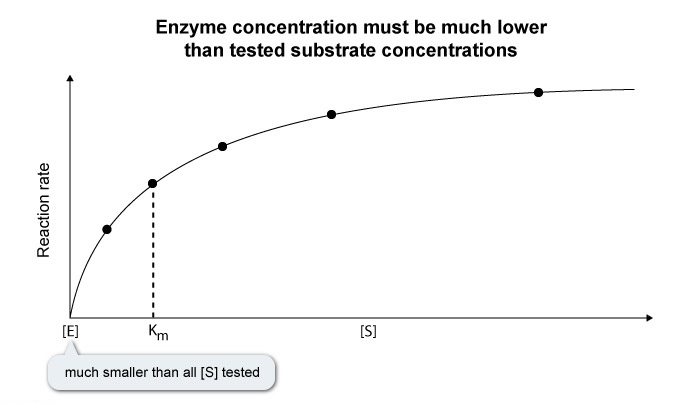
  • To ensure that ES formation does not significantly impact $[S]$$[S]$ , the total concentration of enzyme in solution should be much smaller than any substrate concentration tested

• The steady state assumption states that the concentration of ES remains constant over the course of the reaction , allowing the rate of product formation to remain constant.

  • Once $[S]$$[S]$ becomes significantly depleted , ES levels decrease and the reaction slows.

• The irreversibility assumption states that the reaction proceeds only in the forward direction , and product does not get converted back to substrate.

  • Once enough product accumulates , the reverse reaction occurs at non-negligible levels and further slows the net rate of product formation.

• Each of these assumptions holds true only during the initial phase of the reaction , before substrate is depleted or product accumulates.

• Therefore , for each substrate concentration measured , only the initial reaction rate should be reported.

• $K_m$$K_m$ is the substrate concentration at which $\frac{V_{max}}{2}$$\frac{V_{max}}{2}$ occurs.

• Because enzyme concentration must be substantially smaller than all substrate concentrations tested , enzyme concentration must be much smaller than $K_m$$K_m$ , not larger.

• The Michaelis-Menten equation models the initial rates of a reaction at various substrate concentrations.
• Rates are measured as the slope of the initial , linear phase of the reaction before substrate is depleted and product accumulates.
• Enzyme concentration should be much lower than all substrate concentrations tested.

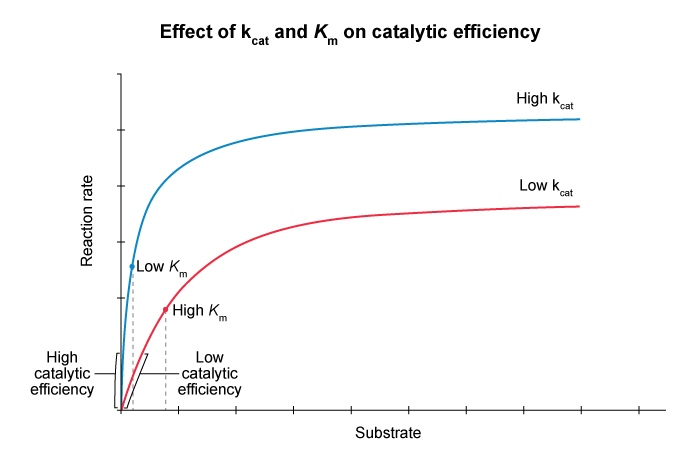
Catalytic Efficiency

• Catalytic efficiency is a measure of how well an enzyme facilitates reactions at low substrate concnetrations.

• When enzyme concentration is held constant , catalytic efficiency is proportional to the initial slope of a Michaelis-Menten curve

  • when $[S]<<K_m$$[S] << K_m$

• This slope is governed by both the catlytic turnover $k_{cat}$$k_{cat}$ and the Michaelis constant $K_m$$K_m$

• Mathematically , catalytic efficiency is calculated as the ratio of $k_{cat}$$k_{cat}$ to $k_m$$k_m$

• An increase in $k_{cat}$$k_{cat}$ increases the catalytic efficiency , and a decrease in $K_m$$K_m$ also increases the efficiency.

• Therefore , an allosteric activator that both increases $k_{cat}$$k_{cat}$ can decreases $K_m$$K_m$ will increase the catalytic efficiency of an enzyme.

• Conceptually , a large ( steep ) slope indicates an efficient enzyme because a small amout of substrate yields a high reaction rate.

• Catalytic turnover ( $k_{cat}$$k_{cat}$ ) measures the number of substrate molecules converted to product per enzyme per second when the enzyme is saturated

  • Therefore , a high $k_{cat}$$k_{cat}$ corresponds to a high maximum rate ( $V_{max}$$V_{max}$ )

    • and , by extension a larger slope at lower substrate concentrations

• The Michaelis constant ( $K_m$$K_m$ ) is an indicator of binding affinity.

• A small $K_m$$K_m$ indicates high affinity , allowing the reaction to approach $V_{max}$$V_{max}$ more rapidly ( higher slope ) with smaller amounts of substrate.

  • Therefore , a small $K_m$$K_m$ contributes to high catalytic efficiency.

#concept , #equation , #kinetic , #rate-law