Lecture 4

Readings

http://umdberg.pbworks.com/w/page/73084145/Why%20entropy%20is%20logarithmic%20%282013%29

http://umdberg.pbworks.com/w/page/73084340/A%20way%20to%20think%20about%20entropy%20--%20sharing%20%282013%29

Logarithmic Entropy

• $S=k_B\ast ln(W)$$S = k_B * ln(W)$

• If you combine 2 systems, you can add entropy $S$$S$

• THe number of possible microstates for combined system is the product of the numbers of microstates (W) of the 2 separate systems.

• Choose $M$$M$ out of $N$$N$ objects, and don't care about order.

• How many different sets?

  $$\frac{N!}{(N-M)!\ast M!}$$

• Obtain 3 heads out of 7 flips

• Number of ways to end up with 3 steps to right out of 7 total steps

• Number of ways for 3 balls to end up in 7 boxes

Entropy as Sharing

• Entropy is like tempearture, pressure, and concentration

• It's a course, overview idea that doesn't care about specific molecules at specific times

• The following four statements are all equivalent due to 2nd Law:

  • A system wants to move towards thermodynamic equilibrium

  • A system wants to move toward the state with the greatest entropy

  • A system randomly choses a macrostate with lots of microstates

    • Because there's so many of these particular microstates

  • A system wants to spread energy evenly among all its degrees of freedom

Counting Probability vs. Distributions

• In this class, we look at probabilites for 3 different systems:

  1. Coin flips
  2. Diffusion of molecules
  3. Putting energy packets into degrees of freedom

• In each system, there is a "probability" view, and a "distribution" view

• Coin Flipping:

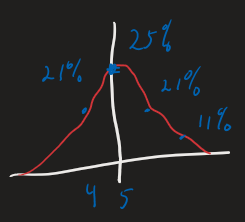
  • Probability View - Flip 1 coin 10 tiems.

    • Microstate = specific sequence of heads and tails
    • Macrostate = total number of heads
    • You can calculate the probability of any particular macrostate for this 10 flips.
    • The probability depends on the number of ways to get that number of heads

  

   

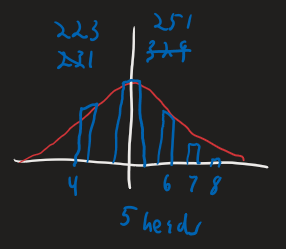
  • Distribution View - Flip 1000 coins, 10 times each.

    • Microstate = How many times heads came up on each coin

      • For example, coin 1 had 4 head flips, coin 2 had 7 heads, etc.

    • Macrostate = a particular distribution of the number of heads

      • For example, 4 heads came up on 223 coins, 5 heads came up on 251 coins, etc.

    • This distribution is highly likely to be similar to the probability found in the probability view.

    • As you increase the number of coins used, the distribution becomes fore and more like the probability view

• Molecule Diffusion

  • Probability View - 1 molecule takes 10 steps

    • Microstate = a specific sequence of steps, L R R 0 L L etc
    • Macrostate = final location of the 1 molecule
    • You can calculate the probability of any particular final location

  • Distribution View - 1000 molecules, each takes 10 steps

    • Microstate = final location of each molecule.

      • For example, molecule 1 ended up at -3 , molecule 2 ended up at +4 , etc

    • Macrostate = a particular distribution of the final locations.

      • For example, 147 molecules ended up at -3 , 238 ended up at +1 , etc

    • This distribution is highly likely to be similar to the probability found in the probability view.

    • As you increase the number of molecules, the distribution becomes more and more like the probability view

• Energy Packets and Degrees of Freedom for 2 Objects

  

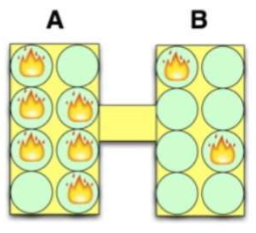
  • Probability View - 1 set of 2 objects with say 8 energy packets

    • Microstate = a particular arrangement of each of the multiple energy packets among all the degrees of freedom in the 2 objects

    • Macrostate = the number of energy packets in each object

      • For example, 6 in the left object and 2 in the right object

    • You can calculate the probability of any particular macrostate by counting the number of ways to arragne the packets to create each macrostate.

      • Assumption: each degree of freedom is equally likely

  • Distribution View - 1000 sets of 2 objects, with each set having 8 energy packets spread between the 2 objects

    • OR , observe 1 set of the 2 objects at 1000 different time points.

    • Microstate = the specific division of energy packets at each observation

      • For example, 1st set/time point has 5 energy on left and 3 on right; 2nd set/time point has 4 on left and 4 on the right, etc

    • Macrostate = a particular distribution of the energy packet divisions

      • For example, 3L and 5R occurred 265 times, 4L and 4R occurred 341 times, etc

    • This distribution is highly likely to be similar to the probability found in the probability view.

    • As you increase the number of set/time points, the distribution becomes more and more like the probability view

Main Message

• We spend a lot of time calculating the probability of various arrangements for 1 molecule/set of objects.

• This is because the probability matches up with what the system will look like if you have a large number of molecules and/or give the system enough time

• This is the 2nd Law of Thermodynamics

• In reality, you've got trillions * trillions of molecules, or trillions * trillions of energy packets, each doing their own random choices

• The number of ways to get certain macrostates is much, much higher than other macrostates, so the system moves toward the likely macrostates.

• And the macrostate for these trillions * trillions is a distribution

• 6 million energy packets on the left and 2 million energy packets on the right is an extremely unlikely macrostate.

  • So the system (if they are isolated from the surroundings and in thermal contact) will head towards something close to 4 million on the left and 4 million on the right.
  • It will fluctuate and won’t always be exactly 4 million each.

• Whenever you observe the system, the macrostate you find will be randomly chosen from all possible macrostates, but according to the probability of each.

  • But the sun will go out before you ever find the system with 6 million on the left and 2 million on the right.