Lecture 2

Readings

http://umdberg.pbworks.com/w/page/63045403/Organizing%20the%20idea%20of%20energy%20%282013%29

http://umdberg.pbworks.com/w/page/63045599/Enthalpy%20%282013%29

Energy Types

• For coherent motion, applies to macroscopic objects
• Microscopic objects can also move coherently
• Incoherent ( random ) motion is also a form of kinetic energy, but this is usually grouped under "thermal" or "chemical" energy.

• Can exist at macroscopic or microscopic scale

• At microscopic scale ( bonds ), the Lennard-Jones potential is used as approximate potential energy shape.

  • But microscopic potential energy is usually grouped under "chemical energy"

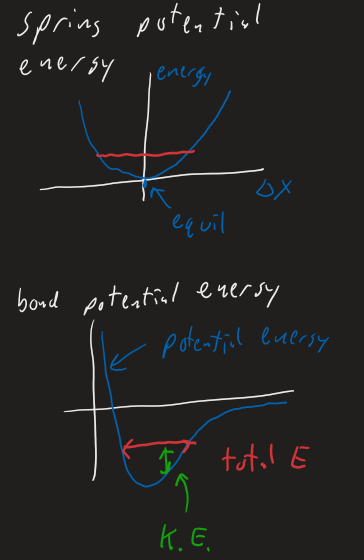
• Kinetic and Potential Energy of atoms and molecules ( but not electrons )
• Random motion
• Not focusing on single atom or molecule, but looking at overall "random jittering" of the atoms of the entire object

• Kinetic and potential energy of electrons in an atom or molecule

• Basically, bonds

  • Covalent Bonds = deep wells
  • Hydrogen bonds = medium
  • Van der Waals bonds = shallow

Enthalpy

http://umdberg.pbworks.com/w/page/63045599/Enthalpy%20%282013%29

• General question - "How much energy must be added (or removed) to make a system change from state A to state B?"

  • "State" often referes to specific chemicals
  • State A might be one side of a chemical reaction, and state B the other side
  • Or State A might be liquid water, and state B might be $H_{2}O$$H_2O$ vapor

• To answer the question, you also need to specify external conditions such as pressure, volume, and/or temperature

• So to be more precise, the question is "How much energy is needed to go":

  • From: State A at $P_A$$P_A$ , $V_A$$V_A$ , and $T_A$$T_A$
  • To: State B at $P_B$$P_B$ , $V_B$$V_B$ , and $T_B$$T_B$
  • Via a particular path between state A and state B, where the "path" is sequence or restriction of P, V, and T

• Enthalpy is the energy question when Pressure stays constant

  • So, From: State A at $P_A$$P_A$ , $V_A$$V_A$ , and $T_A$$T_A$
  • To: State B at $P_B$$P_B$ , $V_B$$V_B$ , and $T_B$$T_B$

• Constant presure is very common in biology and chemistry because often system is open to air.

  • That's why we focus on enthalpy

• Constant pressure means volume can change

  • So you might have to put in extra energy if Velocity increases , or less energy if Velocity degreases compared to a constant volume processs

• If the state has to push against air pressure, the stat it is using up some energy to do that pushing

Basic Problems

• Goal is to compare the energy required to simply break a bond in a vacuum ( the dissociation energy ) to the energy required to break a bond if it's part of a system at constant pressure and temperature ( the enthalpy version of energy )
• First, units issues.
• Three energy units: calories, Joules, and eV ( electron-volts )
• Here are the conversion factors:

A. If a particular molecule has a bond dissociation energy of 1 eV, how much energy would be needed (in kJ = kilo Joules) to break all the bonds in one mole of molecules -- counting no energy for interactions with the environment? Remember, $1mole=6.022\ast {10}^{23}moleculesoratoms$$1\ mole = 6.022*10^{23} molecules\ or\ atoms$

B. For a single $H_2$$H_2$ molecule , $\mathrm{H}{\phantom{X}}_2⟶2\mathrm{H}$$\ce{H2->2H}$ , the dissociation energy is 4.52 eV. How much energy would have to be put in ( in kJ ) to dissociation a mole of hydrogen molecules?

C. Suppose we are putting in energy to dissociate a bubble consisting of 1 mole of hydrogen molecules at STP ( p = 1 atmosphere = $\frac{{10}^{5}Newtons}{mete{r}^2}$$\frac{10^{5} Newtons}{meter^2}$ and T = 300 K ). As we put in energy to dissociate the hydrogens, some of the energy we put in will go into expanding the bubble, some will heat up the gas and some energy will flow out to maintain T = 300 K. Calculate the factor $p\ast \mathrm{\Delta }V$$p*\Delta V$ needed to find the enthalpy change by using the ideal gas law, $p\ast V=n\ast R\ast T$$p*V = n *R *T$ , where $n$$n$ is the number of moles of gas.

• $P\ast \mathrm{\Delta }V$$P*\Delta V$ is an energy

D. What is the total enthalpy change ( in kJ/mol ) for the dissociation of a mole of hydrogen gas at STP? How does this compare to the dissociation energy for that mole of gas? Does it make sense that sometimes the enthalpy is described without paying attention to the volume change? From the reading, remember that enthalpy is given by: $\mathrm{\Delta }H=\mathrm{\Delta }U+(p\ast \mathrm{\Delta }V)$$\Delta H = \Delta U + \left( p * \Delta V \right)$