Hemodynamics - And Combined Concepts

https://34353.org/wi/Physics/cd3d31cca41f66a4eb68645c4dabf854

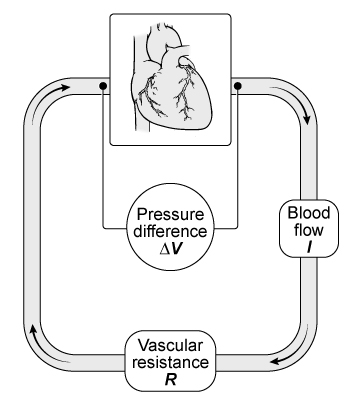
• Blood flow through the cardiovascular system can be modeled as an electric circuit :

  • blood = electricity
  • blood vessels = resistive wires
  • heart = battery

• Ohm's law states that the voltage drop $\Delta V$ across each element , the current $I$ flowing through it , and its electrical resistance $R$ are related by $\Delta V = I * R$

• In a blood vessel , we can replace the components of Ohm's Law with :

  • $\Delta V$ = Pressure difference between one vessel and the next ( $\Delta P$ )
  • $I$ = Volumetric blood flow ( $Q$ )
  • $R$ = Vascular Resistance $R$

$$\Delta P = Q * R \tag{1}$$

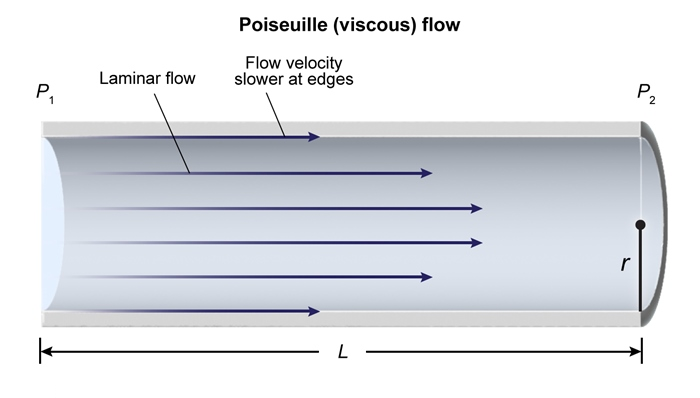
• Vascular resistance is due to the blood's viscosity ( $\eta$ ) and the dimensions of the vessel through which it flows.
• Assuming blood vessels are cylinders , $R$ can be approximated as :

$$R = 8 * \eta * L * \pi * r * 4$$

$$R = \frac{8 * \eta * L}{\pi * r^4} \tag{2}$$

• Where $L$ is the length of the vessel , and $r$ is its inner radius.
• If Equation 2 is combined with Equation 1 , the resulting equation is Poiseuille's Law :

$$\Delta P = Q * \left(\frac{8 * \eta * L}{\pi * r^4}\right)$$

• Poiseuille's Law describes the laminar flow ( no turbulence ) of a viscous , incompressible fluid through a pipe.
• The viscosity of a fluid measures the internal frictional force that resists the flow.
• A fluid is incompressible if its density and volume do not change appreciably due to changes in pressure.

$$Q = \frac{\Delta P}{R} = \frac{\pi * r^4 * \Delta P}{8*\eta * L}$$

• The greatest decrease in blood flow rate is achieved when the radius is reduced by a factor of 2 , because Poiseuille's Law has a fourth-power dependence on $r$ and a linear ( first-power ) dependence on all the other variables.
• The change in radius yields :

$$\left(\frac{r}{2}\right)^4 = \frac{r^4}{2^4} = \frac{r^4}{16}$$

• Therefore , blood flow rate $Q$ decreases by a factor of $16$ when the vessel's radius $r$ is halved.

• Poiseuille's Law is used to model fluid flow in pipes, assuming laminar flow of viscous and incompressible fluids.
• According to Poiseuille's Law, the flow rate is directly proportional to vessel radius and pressure difference, and inversely proportional to viscosity and vessel length.

• The units of a variable in an equation can be determined from the units of the other variables.

• Viscosity ( $\eta$ ) is used in Equation 2.

  • However, the units of vascular resistance $R$ are unknown.

• Because the units of $R$ can be determined from Equation 1 , the two equations are combined to eliminate $R$

$$\frac{8 * \eta * L}{\pi * r^4} = \frac{\Delta P}{Q}$$

• To determine the units of $\eta$ , the other variables are rewritten with their SI units of length ( $L$ ) and radius ( $r$ ) in meters ( $m$ )

  • Pressure change ( $\Delta P$ ) in pascals ( Pa ) , and volumetric flow rate ( $Q$ ) in cubic meters per second $\frac{m^3}{s}$

• Note , that $8$ and $\pi$ are dimensionless quantities ( they have no units ).

$$\frac{\eta * [m]}{[m^4]} = \frac{[Pa]}{[\frac{m^3}{s}]}$$

• Solving for $\eta$ and simplifying :

$$\eta * [m] = \frac{[Pa]*[m^4]*[s]}{[m^3]}$$

$$\eta = \frac{[Pa]*[m^4]*[s]}{[m^3]*m} = Pa\cdot s$$

• Units of one variable in an equation can be determined by rewriting the other variables using their units and solving for the units of the target variable.

• Vascular resistance is the resistance of a blood vessel that must be overcome for blood to flow ( Equation 1 )

• Equation 1 can be rearranged to $R = \frac{\Delta P}{Q}$ , showing resistance ( $R$ ) is directly proportional to the pressure difference ( $\Delta P$ ) and inversely proportional to flow rate ( $Q$ ).

• Because $Q$ is the same for each vessel , $R$ is dependent ONLY on $\Delta P$.

  • Therefore , the vessel with the greatest $\Delta P$ has the greatest resistance ( $R$ )

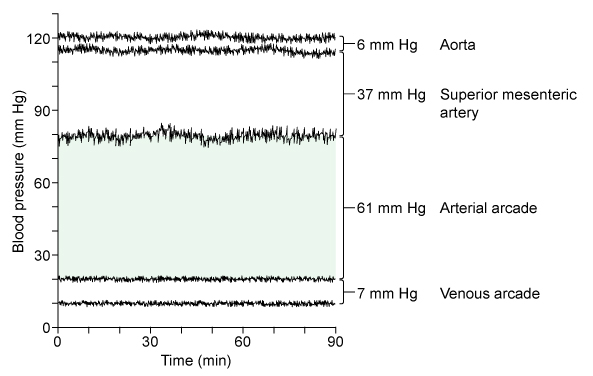
• All pressure measurements int he study were recorded during systole, the point of greatest pressure.

  • Therefore, the pressure drop across a vessel is the difference between its pressure and the pressure of the next vessel.

• These pressure differences are calculated in Figure 2.

• The arterial arcade has the greatest pressure difference of $61\ mm\ Hg$ , and therefore has the greatest flow resistance.

• The vascular resistance of a vessel is directly proportional to pressure difference and inversely proportional to volumetric flow rate.
• When the volumetric blood flow rate is the same in two vessels, the vessel with the greater pressure difference has the greater resistance to flow.

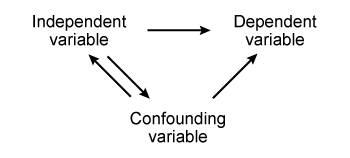
• In an ideal experiment or study, any and all changes in the measured dependent variable are due to changes in the independent variable.

• However, this model may not be realistic due to confounding variables.

  • Confounding variables = uncontrolled variables that have an effect on the dependent variable.

• Experiments should be designed to minimize the influence of confounding variables if they cannot be eliminated.

• To determine the magnitude of any effect of a possible confounding variable on the dependent variable, and experimental group that differs in the suspected confounding variable is tested.

• In the study described int he passage , different blood vessels of rats ( independent variable ) were accessed through an invasive laparotomy procedure ( suspected confounding variable ) to measure mesenteric blood flow pressures ( dependent variable ).
• The inclusion of an alternative procedure that is minimally invasive or noninvasive but still measures mesenteric blood pressures would determine if laparotomy is a confounding variable by determining if differences are found in the measured blood pressures.

• A confounding variable is an uncontrolled variable different form the independent variable but that still has an impact on the dependent variable.
• The effect of a confounding variable can be observed by including a group that differs in the confounding variable.

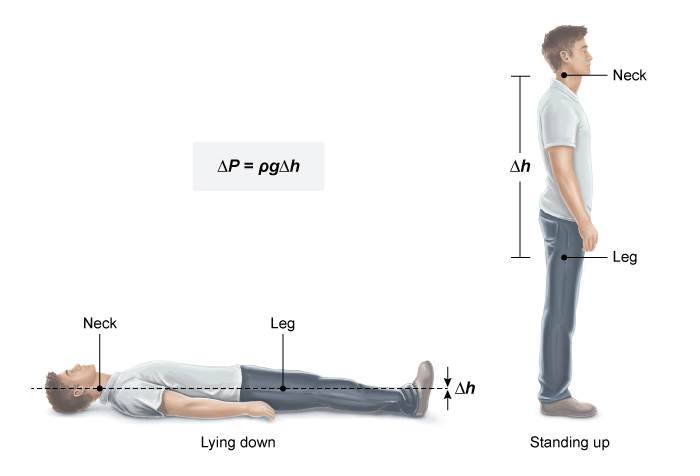
• The pressure exerted by the weight ( potential energy ) of a fluid is direclty proportional to its depth.

  • This pressure is known as hydrostatic pressure.

• The hydrostatic pressure difference ( $\Delta P$ ) between any two points in a fluid is found by :

$$\Delta P = \rho * g * \Delta h$$

• where $\rho$ is the density of the fluid , $g$ is the acceleration due to gravity , and $\Delta h$ is the vertical displacement between the locations where the initial and final pressures are measured.

• When the person is lying down, the neck and the leg are at about the same height level , making $\Delta h$ negligible.

• However, when the person stands up , the $\Delta h$ between the nexk and the leg increases significantly.

  • The blood pressure difference increases due to the hydrostatic pressure of the column of blood from above the leg to below the neck.

• Hydrostatic pressure is the pressure exerted by the weight ( potential energy ) of a fluid.
• The hydrostatic pressure difference between two points in a fluid is proportional to the fluid's density , the gravitational acceleration , and the vertical displacement between two points.

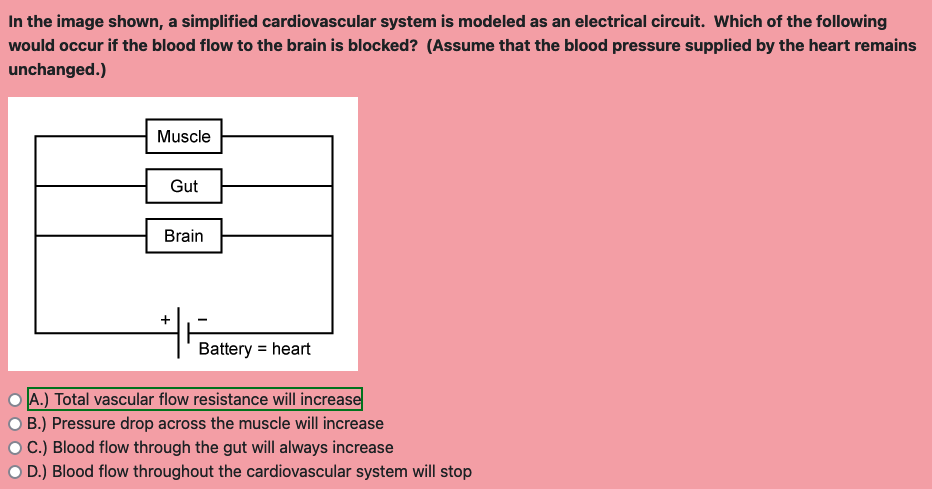
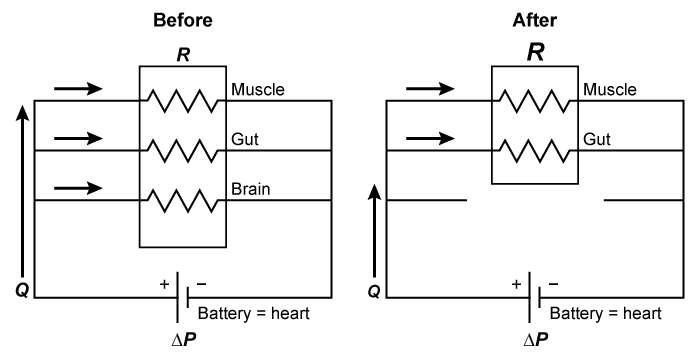
• The three biological components ( resistors ) shown in this model make a parallel circuit, and the heart ( battery ) generates the pressure difference ( voltage ) that drives the blood flow ( current ).

• The equivalent resistance ( total vascular flow resistance ) will increase with the removal of a resistor ( the brain ) because it is in parallel with the other components.

• The voltage drop across each resistor will be equal to that of the battery, which does not change.

• The current through each resistor in a parallel circuit is related only to the intrinsic resistance of the resistor an dthe electric potential ( voltage ).

  • Vascular resistance of the gut and systemic blood pressure both remain constant after obstructing blood flow to the brain, so blood flow through the gut does not change.

• If this were a series circuit, in which the current flows only through one path, all flow would stop by blocking one element.

  • Parallel circuits have more than one path through which the current can flow.

• For resistors in parallel, the voltage drop across each resistor is the same.
• The equivalent resistance increases if a resistor is removed.
• The current through each resistor in parallel is independent from the others, and the sum of each component current equals the total current.

#blood , #ohms-law , #circuit , #model , #equation , #flow